ド・モルガンの法則とは
ド・モルガンの法則は命題(TrueまたはFalseが入るboolean型だと考えてください)$P$、$Q$、論理和(or)を$\cup$、論理積(and)を$\cap$、$P$の否定(not)を$\overline{ P }$とすると以下の式で表されます。
\overline{ P \cup Q } = \overline{ P } \cap \overline{ Q }\cdots① \\
\overline{ P \cap Q } = \overline{ P } \cup \overline{ Q }\cdots②
①の式は「$P$または$Q$の否定」が「$P$の否定かつ$Q$の否定」と等しい、②の式は「$P$かつ$Q$の否定」が「$P$の否定または$Q$の否定」と等しいという事を示しています。
コーディングでの使用例
ド・モルガンの法則は条件式を簡略化するために役に立つ場合があります。
以下のサンプルコードは全てPython3系です。
期間の重複を判定する
例えば以下のような判別を行うメソッドを実装する場合を考えます。
判定内容
2つの期間A、Bの開始と終了a_start、a_end、b_start、b_endがそれぞれ与えられたとき、期間に重複があればTrue、重複がなければFalseを返す。期間A、Bはそれぞれ閉区間とする(a_end == b_startがTrueの場合は重複として扱う)。
入力
- a_start : 期間Aの開始(int型)
- a_end : 期間Aの終了(int型)
- b_start : 期間Bの開始(int型)
- b_end : 期間Bの終了(int型)
ただし、a_start < a_end、b_start < b_endであることは保障されているものとする。
出力
- 重複していればTrue、そうでなければFalse(boolean型)
通常の実装
4つの入力がどのような関係であれば「重複している(True)」といえるかを考えます。
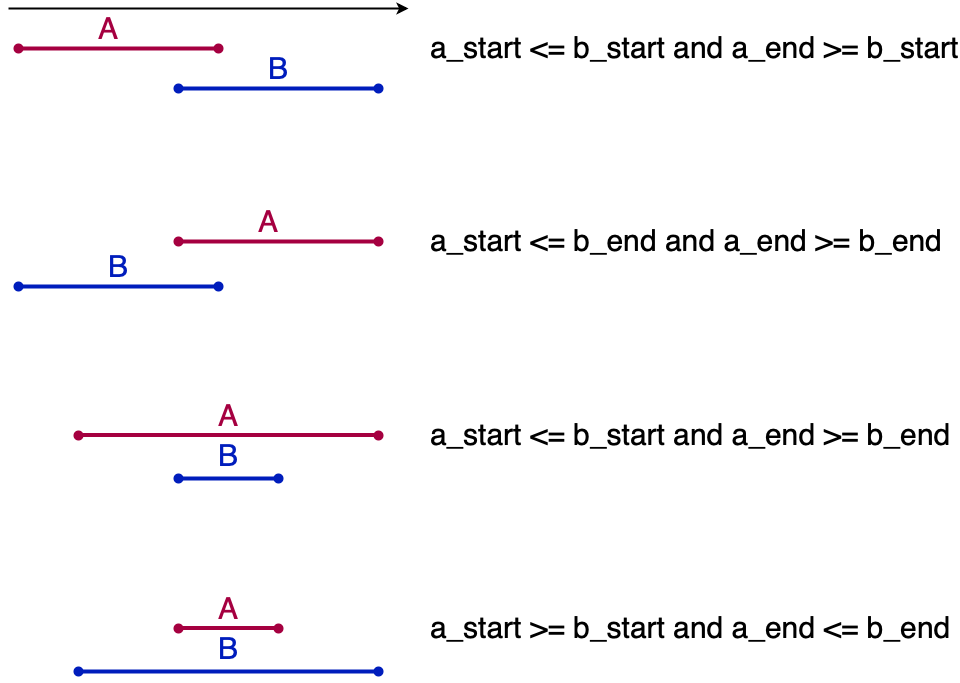
重複しているA、Bは以下の図のいずれかのパターンであると言えます。
これらのいずれかであると判定する場合は以下のようなメソッドになります。
def is_duplicate (a_start, a_end, b_start, b_end):
return (a_start <= b_start and a_end >= b_start) \
or (a_start <= b_end and a_end >= b_end) \
or (a_start <= b_start and a_end >= b_end) \
or (a_start >= b_start and a_end <= b_end)
print(is_duplicate(1, 3, 2, 4)) # 重複する
print(is_duplicate(2, 4, 1, 3)) # 重複する
print(is_duplicate(1, 4, 2, 3)) # 重複する
print(is_duplicate(2, 3, 1, 4)) # 重複する
print(is_duplicate(1, 2, 2, 3)) # 重複する
print(is_duplicate(2, 3, 1, 2)) # 重複する
print(is_duplicate(1, 2, 3, 4)) # 重複しない
print(is_duplicate(3, 4, 1, 2)) # 重複しない
実行結果は以下の通りです。
True
True
True
True
True
True
False
False
上記の結果は期待通りの動作をしていることがわかります。しかし、比較演算が8つもあるためバグが混入しやすいコードになってしまいました。
ド・モルガンの法則を用いた実装
上記のアプローチとは逆に「重複していない(False)」状態を考えます。
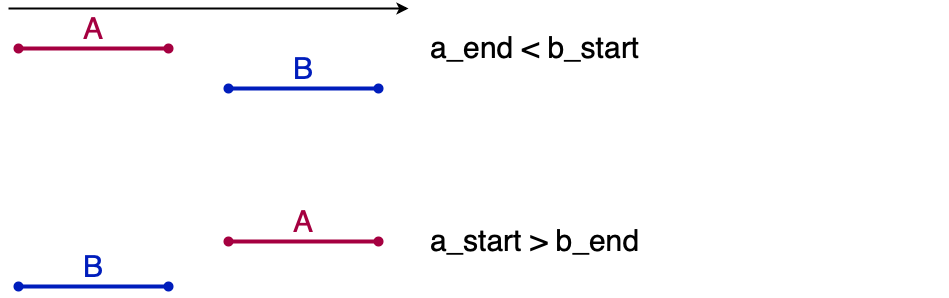
重複していない A、Bは以下の図のいずれかのパターンであると言えます。
「重複していない」とは上記の条件のどちらかの場合であり、その否定は「重複している」状態です。なので、重複している状態とは
\overline{ (\mathrm{a\_end} < \mathrm{b\_start}) \cup (\mathrm{a\_start} > \mathrm{b\_end}) }
であるとも言えます。この式をド・モルガンの法則を用いて変形すると以下の形になります。
\overline{ (\mathrm{a\_end} < \mathrm{b\_start}) \cup (\mathrm{a\_start} > \mathrm{b\_end}) } \\
= \overline{(\mathrm{a\_end} < \mathrm{b\_start})} \cap \overline{(\mathrm{a\_start} > \mathrm{b\_end})}
$ \overline{(\mathrm{a\_end} < \mathrm{b\_start})} $ と $ \overline{(\mathrm{a\_start} > \mathrm{b\_end})} $はそれぞれ以下のように変形できます。
\overline{(\mathrm{a\_end} < \mathrm{b\_start})} = (\mathrm{a\_end} \geqq \mathrm{b\_start}) \\
\overline{(\mathrm{a\_start} > \mathrm{b\_end})} = (\mathrm{a\_start} \leqq \mathrm{b\_end})
よって、「重複していない」を否定した「重複している(重複していなくない)」は以下の式で表されます。
(\mathrm{a\_end} \geqq \mathrm{b\_start})\cap(\mathrm{a\_start} \leqq \mathrm{b\_end})
この条件で判定する場合は以下のようなメソッドになります。
def is_duplicate (a_start, a_end, b_start, b_end):
return a_end >= b_start and a_start <= b_end
print(is_duplicate(1, 3, 2, 4)) # 重複する
print(is_duplicate(2, 4, 1, 3)) # 重複する
print(is_duplicate(1, 4, 2, 3)) # 重複する
print(is_duplicate(2, 3, 1, 4)) # 重複する
print(is_duplicate(1, 2, 2, 3)) # 重複する
print(is_duplicate(2, 3, 1, 2)) # 重複する
print(is_duplicate(1, 2, 3, 4)) # 重複しない
print(is_duplicate(3, 4, 1, 2)) # 重複しない
上記のコードの実行結果は以下の通りです。
True
True
True
True
True
True
False
False
この結果から分かる通り、式の変形を行わなかった実装と同じ結果でかつ比較演算が少ない実装にすることができました。
まとめ
Trueの場合の条件が複雑な場合はFalseの場合の否定を考えると条件が簡略化される場合がある