Introduction
Dogelog Player has now arrow functions using a (=>)/2 operator. The semantics is different from other offerings and based on ISO core standard witness calculation [7.1.1.4]. Its genesis is tied to formerly Jekejeke Prolog where we already experimented with this semantics.
Departing from formerly Jekejeke Prolog we also provide ahead of time compilation. It turns out that this gives a better semantics, that can solve problems such as mutual recursion and nested arrows. We present a refinement for interpretative use, that shares the same properties.
Variant Keys
To arrive at the interpreted refinement we had a closer look at what the ahead of time compilation does. An arrow function (X,Y) => Y is X+J, with the free variable is compiled into closure 0rReference(J) where 0rReference is an anonymous predicate with the clause (J,X,Y) :- Y is X+J.
The main idea behind our new arrow interpretation is to use a preprocessor, that represents a clause and thus an anonymous predicate as a ground Prolog term. Our idea is to turn a clause into a variant key. Prologers might be familiar with the idea of variant keys:
freeze_term(X, Y) :-
copy_term(X, Y),
numbervars(Y, 0, _).
Comparing variant keys is an easy method to realize the binary (=@=)/2 operator. Its purpose is to check whether two Prolog terms are a variant of each other. Basically establishing that there is a variable bijection, rendering the terms syntactically equivalent.
:- op(700, xfx, =@=).
X =@= Y :-
freeze_term(X, K),
freeze_term(Y, J),
K == J.
Works as expected:
?- p(X,Y) =@= p(A,A).
fail.
?- p(X,Y) =@= p(A,B).
true.
Clause Instantiation
Modelling clauses as variant keys leaves still some questions open. For example how should we instantiate clauses with fresh variables? We now enter a territory that is probably lesser known to Prologers. In Dogelog Player we have a predicate unnumbervars/3 that does the inverse of numbervars/3. We can use it to define:
melt_term(X, Y) :-
unnumbervars(X, 0, Y).
?- freeze_term(p(X,X), Y), melt_term(Y, Z).
Y = p(A, A),
Z = p(_A, _A).
We can use the above to write a vanilla meta interpreter, to illustrate how this leads to variable clause instantiation. The predicate solve/2 takes a goal and a list of frozen clauses. When invoking a goal that is not a conjunction or true, we search the frozen clauses by melting them:
solve((A,B), P) :- !, solve(A, P), solve(B, P).
solve(true, _) :- !.
solve(H, P) :- member(X, P), melt_term(X, (H :- B)), solve(B, P).
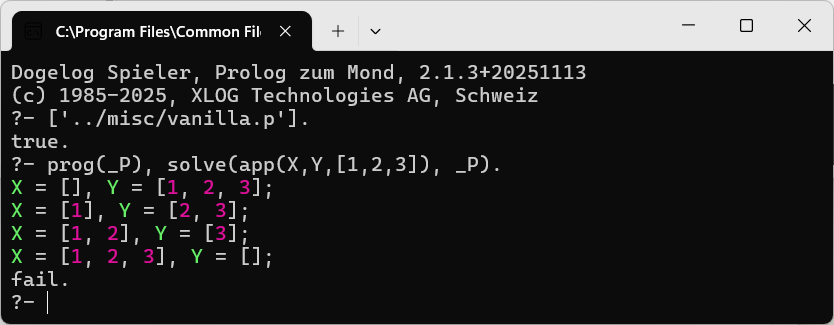
We create our example program via prog/1:
prog([C,D]) :-
freeze_term((app([], X, X) :- true), C),
freeze_term((app([X|Y], Z, [X|T]) :- app(Y, Z, T)), D).
The app/1 for append works as expected:
Closure Construction
Nested functions have become quite popular in programming languages such as Python and JavaScript. They allow sharing some local context from the outer function inside an inner function, without the hussle of passing around parameters. More impressive inner functions can be returned as values and can then serve as closures for their outer context.
We can now try the same with our interpreted arrows as they are already in the pre-view release 2.1.3 of Dogelog Player. First we define a predicate test/1 that creates an adder, with a free variable. This free variable will be captured in the returned closures. The preprocessor creates closures of the form '$ANON'/n that record some extra data besides head and body.
test(C, AddC) :-
AddC = ((X,Y) => Y is X+C).
?- test(2, Add2), write_canonical(Add2), nl.
'$ANON'(''('$VAR'(0), '$VAR'(1), '$VAR'(2)), 0, is('$VAR'(2), +('$VAR'(1), '$VAR'(0))), 2)
As can be seen in the above among the extra data is the free variable which gets capture into the trailing arguments of '$ANON'/n. The predicate is variadic reflecting the number of free variables. The closure created by the preprocessor works as expected. That the closure can be used multiple times during maplist/n can be understood by clause instantiation:
?- test(2, _Add2), maplist(_Add2, [1,2,3], L).
L = [3, 4, 5].
?- test(3, _Add3), maplist(_Add3, [1,2,3], L).
L = [4, 5, 6].
We can add a further indirection, and define closure that is a factory for the adder. This will further demonstrate that arrow functions in a Prolog system give traits of nested functions. The example also shows a form of currying, i.e. functions that return functions and thus gradually reduce the number of arguments, only the terminology is more OO-ish with factory:
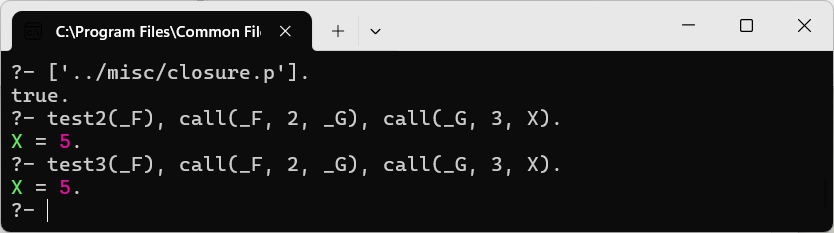
test2(FactoryAddC) :-
FactoryAddC = ((C,AddC) => test(C, AddC)).
test3(FactoryAddC) :-
FactoryAddC = ((C,AddC) => AddC = ((X,Y) => Y is X+C)).
?- test2(F), write_canonical(F), nl.
'$ANON'(''('$VAR'(0), '$VAR'(1)), 0, test('$VAR'(0), '$VAR'(1)))
?- test3(F), write_canonical(F), nl.
'$ANON'(''('$VAR'(3), '$VAR'(4)), 3, =('$VAR'(4), '$ANON'(''('$VAR'(0), '$VAR'(1), '$VAR'(2)), 0, is('$VAR'(2), +('$VAR'(1), '$VAR'(0))), '$VAR'(3))))
The listing shows how we deal with nested arrow functions. While the test2/1 factory calls the closure constructor test/2 in its body, and has a rather straight forward '$ANON'/n representation. The test3/1 factory has as extra data the index 3, because its body has another nested arrow function. This index is then used in unnumbervars/3. Both approaches work as expected:
Conclusions
Nested functions have become quite popular in programming languages such as Python and JavaScript. More impressive inner functions can be returned as values and can then serve as closures for their outer context. Starting from variant keys and a new unnumbervars/3 predicate, we demonstrate the same for our preprocessed and then interpreted '$ANON'/n compounds.