概要
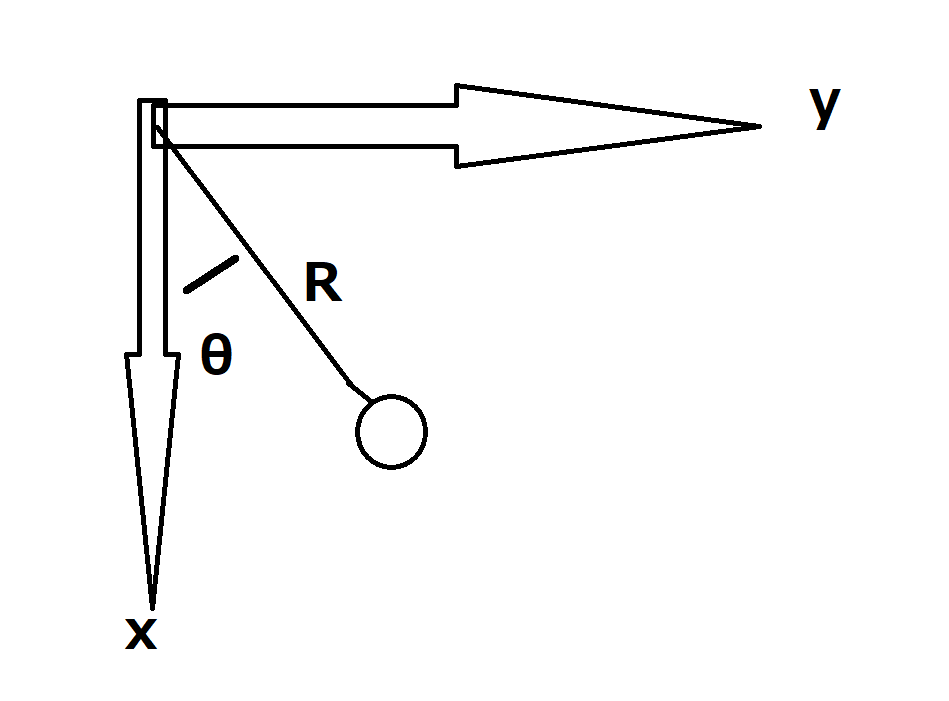
次のような振り子に、
- 角度を調べるためのエンコーダ:分解能1deg
- 振り子のに角速度、加速度センサー
を付けたシステムで、角速度、加速度センサーのみから、角度を推定し、エンコーダーと比較してどれだけ正確に推定できたかを確認する。

数学モデル
Position_x =Rcos\theta \\
Position_y =Rsin\theta \\
Velosity_x = -wRsin\theta \\
Velosity_y = wRcos\theta \\
Accel_x = -w^2Rcos\theta -(dw/dt)Rsin\theta \\
Accel_y = -w^2Rsin\theta +(dw/dt)Rcos\theta \\
となります。
遠心力成分と角加速度による成分によって加速度は定まっていることがわかります。
加速度センサ
重要な事ですが、加速度センサで得られるデータは
(本体の加速度) + (重力加速度)
となります。何故かというと、加速度センサの仕組みは箱にバネを付けてつるしたおもりを用意し、そのバネの長さから加速度を推定するという仕組みだからです。バネの長さは、
- 箱が動くと伸び縮み
- おもりが重力を受ける事で伸び
という二つが有るため2つは別々に関与せずに和として計測されます。
本体が下に自由落下している時、計測される加速度は0です。なぜなら、おもりは下に力を受けバネは縮み、箱は下に加速しバネは伸び、足し合わされ0になります。
よって、ここでわかることは重力加速度の方向と計測加速度の方向は反対方向であると言うことです。実際に計測し、そこら辺の正負は確認すべきですが、私のセンサーと指定した座標系では
Accel_x = +w^2Rcos\theta +(dw/dt)Rsin\theta + Gravity(9.81) \\
Accel_y = +w^2Rsin\theta -(dw/dt)Rcos\theta \\
となりました。これは私が、静止状態の計測加速度の正負で座標系を合わせたため、箱加速度の正負が反転したからでしょう。
以降、混乱しますかも知れませんが、理論加速度*-1+gをAccelとして話を進めます。実際にやってみるという方がいれば、ここら辺は実機あわせで一つ一つ確認することが近道です。
ジャイロセンサ
一方でジャイロセンサはセンサがその場で回転しても、移動しながら回転しても計測データには影響されません。
得られるデータは角速度です。
近似微分器を使用すれば角加速度に変換できます。2階以上の近似微分器はノイズが乗りやすく、元データの数値分解能が高くないと失敗する可能性が高いです。
推定システム
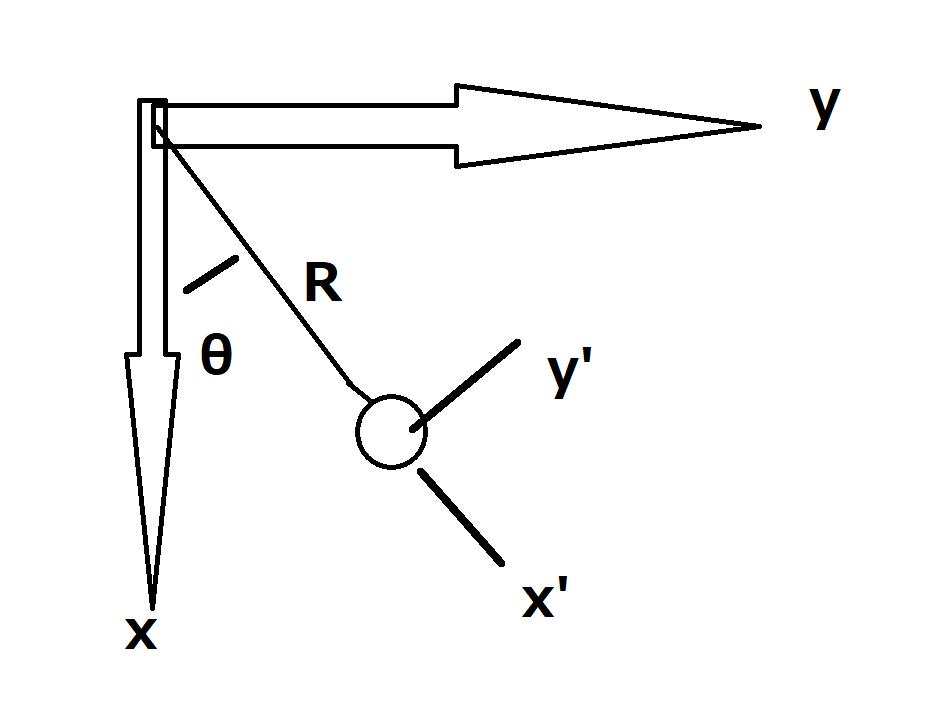
センサー自体も回転するので、観測される加速度は回転する必要があります。
座標系をθ回転 = ベクトルを-θ回転 より (今後 sin = S,cos = Cとします)
\begin{bmatrix}
Accel_x' \\
Accel_y'\\
\end{bmatrix} =
\begin{bmatrix}
C\theta & S\theta \\
-S\theta & C\theta\\
\end{bmatrix}
*
\begin{bmatrix}
Accel_x \\
Accel_y\\
\end{bmatrix}
=\begin{bmatrix}
-Rw^2 + gC\theta \\
(dw/dt)R - gS\theta\\
\end{bmatrix}
となります。
w:角速度はジャイロより得られ、
(dw/dt):角加速度はwに近似微分器を掛ければ結構正確な数値が得られ
近似微分については別の記事を書いてるのでそちらで
わかっていないθを推定するには
計測Accel_x',Accel_y' と w,dw/dt より上の式を満たす θ を探せば良いことになります。
ここで、Newton-Raphson法を使用します。
Newton-Raphson法
f(x) = a
を解くのに、f'(x)を求めることで
a-f(x_n) = f'(x_n)*(x_(n) -x_(n+1))
と考えることで、x_(n+1)を求め、これを繰り返すことで解く方法です。
x_0を最初にあてずっぽで与えます。
必ず収束するかはわからないですが・・・
実際に使うと
Accel_x’,Accel_y'をθで偏微分すると
(\partial / \partial \theta)
\begin{bmatrix}
-Rw^2 + gC\theta \\
(dw/dt)R - gS\theta\\
\end{bmatrix}
=
\begin{bmatrix}
-gS\theta \\
- gC\theta\\
\end{bmatrix}
=
\begin{bmatrix}
Jx \\
Jy\\
\end{bmatrix}
ときれいな関数になります。Jx,Jyは置いただけです。
一変数に2つ誤差が取れるので最小二乗法で出します。
\begin{bmatrix}
a \\
b\\
\end{bmatrix}
=
\begin{bmatrix}
Jx\\
Jy\\
\end{bmatrix}*k
の最適解は
k=(a*Jx + b*Jy)/(Jx^2+Jy^2)
となります。重力加速度の式に適用すると
まず、初期θを当てずっぽで与え
\begin{bmatrix}
-Rw^2 + gC\theta \\
(dw/dt)R - gS\theta\\
\end{bmatrix}
より計算加速度を計算し、計測加速度との誤差を出します。
$ a-f(x_n) $ が(計測加速度)- (計算加速度)に相当します。
\begin{math} f'(x_n)(x_(n) -x_(n+1)) \end{math} は J(θn - θ(n+1)) に相当します。
\theta_(n+1) = \theta_n - ((Accel_(x')-計算ax)*Jx + (Accel_(y')-計算ay)*Jy)/(Jx^2+Jy^2)
となります。これを何回か繰り返せば、よい精度で推定できます。
取り付け角誤差がある場合
センサのx軸が振り子の張力方向に正確にない場合を考えます。
センサのx軸をx''軸とします。
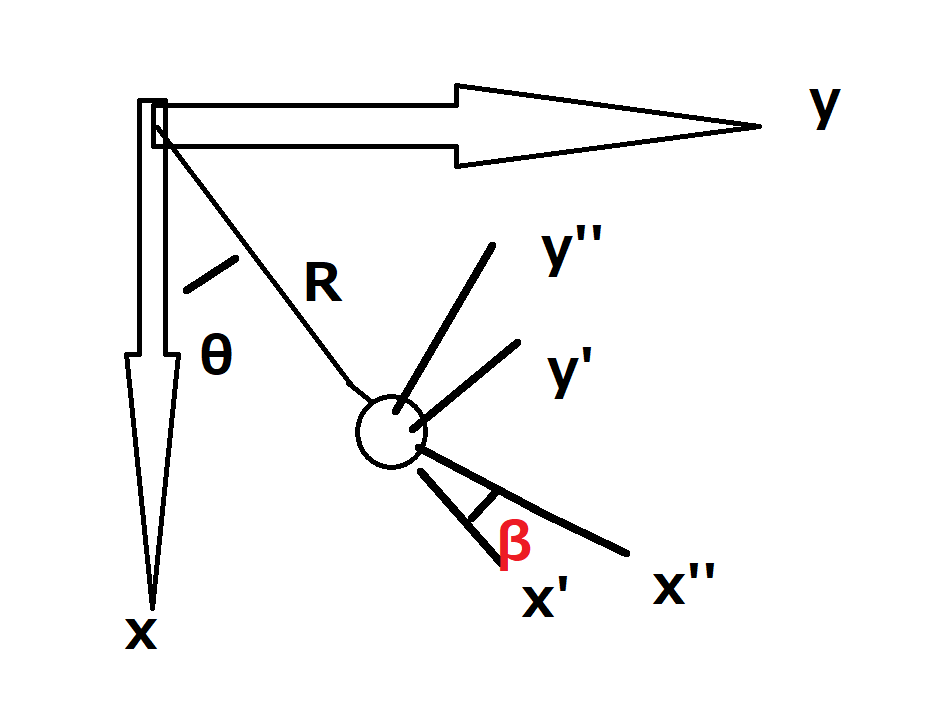
偏角としてβあった場合、x座標系からx''系に見方を変えるときθ+β回転させればよいとわかります。
\begin{bmatrix}
Accel_x'' \\
Accel_y''\\
\end{bmatrix} =
\begin{bmatrix}
C(\theta+\beta) & S(\theta+\beta) \\
-S(\theta+\beta) & C(\theta+\beta)\\
\end{bmatrix}
*
\begin{bmatrix}
Accel_x \\
Accel_y\\
\end{bmatrix} \\
ちょっと書くのがめんどくさくなってきました。
cos(θ+β)=Cθβと書くことにします。
\begin{bmatrix}
Accel_x'' \\
Accel_y''\\
\end{bmatrix} = w^2 R*
\begin{bmatrix}
C\theta\beta*C\theta+S\theta\beta*S\theta \\
-S\theta\beta*C\theta+C\theta\beta*S\theta \\
\end{bmatrix}
+(dw/dt)R
\begin{bmatrix}
C\theta\beta*S\theta-S\theta\beta*C\theta \\
-S\theta\beta*S\theta-C\theta\beta*C\theta \\
\end{bmatrix} \\
+Gravity
\begin{bmatrix}
C\theta\beta \\
-S\theta\beta\\
\end{bmatrix} \\
これをθで偏微分しJを出すと
\begin{bmatrix}
Jx \\
Jy\\
\end{bmatrix} =
\begin{bmatrix}
-Gravity*S(\theta+\beta)\\
-Gravity*C(\theta+\beta)\\
\end{bmatrix}
なんとw,dw/dtによらない結果となります。
同様にニュートンラフソンを使うと出ます。
取付け偏角βと安定角偏差の計測
取付け偏角βは振り子の自由振動の方程式
J(dw/dt) + cw +mgsin\theta = 0
をエクセルでオイラー法(RK4法も有るがソルバーで収束しにくい、正確だが値はそこまで変わらなかった)でシミュレーションし、エンコーダーで計測した角度との誤差の総和を計算し、ソルバーに放り投げてシステム定数を同定し、計測加速度とシミュレーションから導出される加速度の誤差をソルバーに投げてβを推定しました。静止状態の振り子を0°として行いました。
よって、エンコーダーは静止状態を0:基準としたので
これまでの、センサーが一番下に来る角度を0:基準とする方式と偏差が生まれます。この偏差を安定角偏差とするとこちらも推定できます。この後、倒立振子などをする場合は安定角と、計測される角度との差をどれだけ正確に推定できるかが制御を成功できるかの決め手になる気がします。まだできていません。
これをした場合
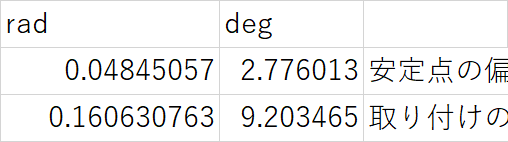
となりました。
仮にエンコーダーがない場合はやっていないですが、、エクセルでシミュレーションした角速度とジャイロの角速度を比較して、初期角度とシステム定数J,mg,cを変数にしてソルバーを解くことになると思います。
また、振り子のように下側に行かず倒れるようなシステムの場合は、手を離してから、床とぶつかるまでで同定することになるでしょう。
システムに導入
#include "mbed.h"
#include "Serial.h"
Serial pc(USBTX, USBRX); // USBシリアルポートのインスタンス
Serial Ro(p9,p10);
Serial Ac(p13,p14);
Serial Cc(p28,p27);
DigitalOut myled(LED1);
DigitalOut check(p18);
InterruptIn css(p17);
float CulculateAngle(float NAngle,float Rax,float Ray,float Rgz,float W2); //Rax:計測加速度
char low=0;
char high = 0;
int Rotate = 0;
bool Polarity = true; //true:負
int DataAbit = 0;
volatile int DataA[16];
int gx;
int gy;
int gz;
int ax;
int ay;
int az;
bool TF = false;
float R[7] = {0,0,0,0,0,0,0}; //単位補正後 角度
float W[6] = {0,0,0,0,0,0}; //角度微分1階と2階
float W2[6] = {0,0,0,0,0,0}; //ジャイロ微分
float GZ[7] = {0,0,0,0,0,0,0}; //単位補正後 ジャイロ
float AngleGyro = 0; //ジャイロよりの角度
float Radi = 0.1; //半径[m]
float Gravity = 9.5839;
float AX;
float AY;
float Rg[7] = {0,0,0,0,0,0,0}; //ジャイロカラの角度:Rg[0]は最初の
float bb = 0.04845057; //rad:取り付け偏差
float rr = 0.160630763; //安定角偏差
//
float NeedCurrent = -0.8;
int n = 0;
void cssf() //加速度センサ 1 p9
{
DataAbit = 0;
}
void getR()
{
//pc.printf("%c ",Ro.getc());
char Rse = Ro.getc();
if((Rse&0b10000000)==0b10000000) { //highByte
high = Rse ;
if((high&0b01000000)==0b01000000) { //値は負なのでそのまま
Polarity = true;
} else { //値は正なので最上位を0にする
high= high & 0b01111111;
Polarity = false;
}
//pc.printf("%3x high",Rse);
} else { //lowByte
low = Rse;
//pc.printf("%3x low",Rse);
Rotate = (high <<7) | low ;
if(Polarity ==true ) { //負の時 int 2byte でないので
Rotate = Rotate|0x8000;
Rotate =( 0xFFFF - Rotate) * (-1) -1 ;
//Rotate = -1* (~Rotate)-1;
}
//pc.printf("%6d \r\n",Rotate);
for(int i = 6; i>=1; i--) {
R[i]= R[i-1];
}
R[0]= Rotate*-1*0.01745329;
}
}
void getA()
{
DataA[DataAbit]= Ac.getc();
DataAbit ++ ;
if(DataAbit == 12) { //全データ
DataAbit = 0;
for(int i = 0; i<6; i++) {
DataA[i]= DataA[i*2]<<8 | DataA[i*2+1];
if( (DataA[i]& 0x8000) == 0x8000) { //負の時
DataA[i] = (0xFFFF - DataA[i] ) *(-1) -1;
}
}
gx = DataA[0];
gy = DataA[1];
gz = DataA[2];
ay = DataA[3] * -1;
ax = DataA[4];
az = DataA[5];
TF = true;
for(int i = 6; i>=1; i--) {
GZ[i]= GZ[i-1];
}
GZ[0]=gz * 2.66316109 * 0.0001 - 0.002066694;
AX = ax * 5.987548 * 0.0001;
AY = ay * 5.987548 * 0.0001;
}
}
void getC(){
char a1 = Cc.getc();
//pc.printf("%5d \r\n",a1);
}
int main()
{
pc.baud(115200);
Ro.baud(115200);
Cc.baud(115200);
Ro.attach(getR,Serial::RxIrq);
Cc.attach(getC,Serial::RxIrq);
Ac.baud(115200);
Ac.attach(getA,Serial::RxIrq);
css.rise(&cssf); //p9
while(1) {
if(TF == true) {
TF = false;
check = 1;
//二回微分 wa = 0.5
W[0] = (17.48374*R[0] +17.48374*R[1] -34.96748*R[2] -34.96748* R[3] +17.48374*R[4] +17.48374*R[5]);
W[0] = W[0]-(-3.4182041*W[1]+4.8518078*W[2]-3.5366809*W[3]+1.3165256*W[4]-0.1994615*W[5]);
//gz の近似微分器wa =3.0
W2[0] = W2[0] = (25.59053*GZ[0] +76.771591*GZ[1] + 51.181061*GZ[2] -51.181061* GZ[3] -76.771591*GZ[4] -25.59053*GZ[5]);
W2[0] = W2[0]-(1.2393125*W2[1]+1.1733521*W2[2]+0.5228261*W2[3]+0.143486*W2[4]+0.0155081*W2[5]);
//ジャイロのみから角度を推定する
//前回の角度から始めて、ジャイロ、角速度が一致する角度を探す
//float CulculateAngle(float NAngle,float Rax,float Ray,float Rgz,float W2) //Rax:計測加速度
Rg[0] = Rg[6];
//Rg[0] = 0;
for(int i = 1;i<=6;i++){
Rg[i]= CulculateAngle(Rg[i-1],AX,AY,GZ[0],W2[0]);
}
pc.printf("%8f ",(Rg[6]-rr)*57.29578);
pc.printf("%8f \r\n",R[0]*57.29578);
//コントローラ設計
//------------更新----------------
for(int i = 5; i>=1; i--) {
W[i]= W[i-1];
}
for(int i = 5; i>=1; i--) {
W2[i]= W2[i-1];
}
check = 0;
}
}
}
float CulculateAngle(float NAngle,float Rax,float Ray,float Rgz,float W2) //Rax:計測加速度
{
float cbb = cos(NAngle+bb);
float sbb = sin(NAngle+bb);
float c = cos(NAngle);
float s = sin(NAngle);
float ccbb = c*cbb;
float csbb = c*sbb;
float scbb = s*cbb;
float ssbb = s*sbb;
float Rggz = Rgz * Rgz;
float axxx = Radi*( (ccbb+ssbb)*Rggz + (scbb-csbb)*W2)+cbb * Gravity;
float ayyy = -1*Radi*( (scbb- csbb)*Rggz + (ssbb+ccbb)*W2) - sbb* Gravity;
float Jx = -1* sbb* Gravity;
float Jy = -1*cbb * Gravity;
//pc.printf("%8f ",axxx);
//pc.printf("%8f ",Rax);
//pc.printf("%8f ",ayyy);
//pc.printf("%8f ",Ray);
float FAngle = NAngle-( (axxx-Rax)*Jx + (ayyy-Ray)*Jy )/(Gravity * Gravity);
//pc.printf("%8f ",FAngle);
return FAngle;
}
こんな感じで関数化し、6回繰り返して計算するしました。
エンコーダーは静止状態を0:基準としたので
これまでの、センサーが一番下に来る角度を0:基準とする方式と定常偏差が発生します。これも、ソルバーで推定しても良いですが今はしません。
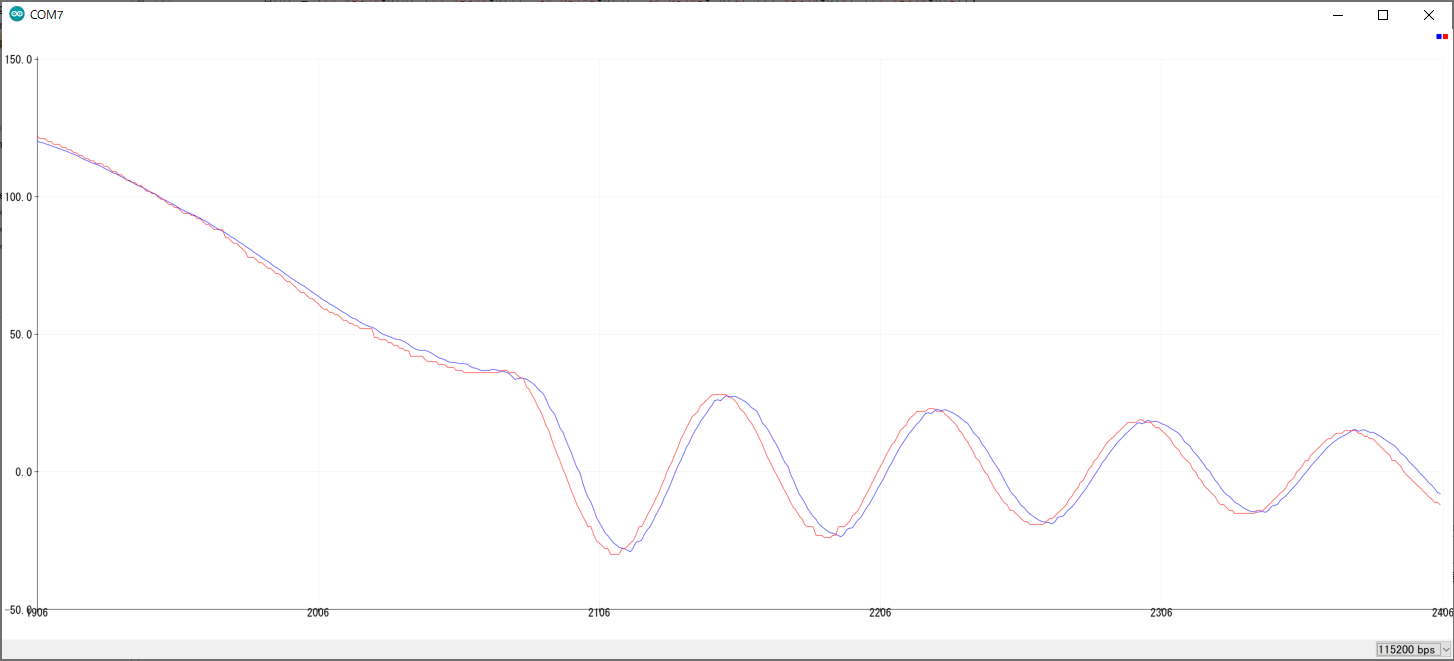
青:ジャイロのみから推定した 赤:エンコーダーによる角度
ジャイロの数値は3サンプル0.03sだけ遅れが有ります。
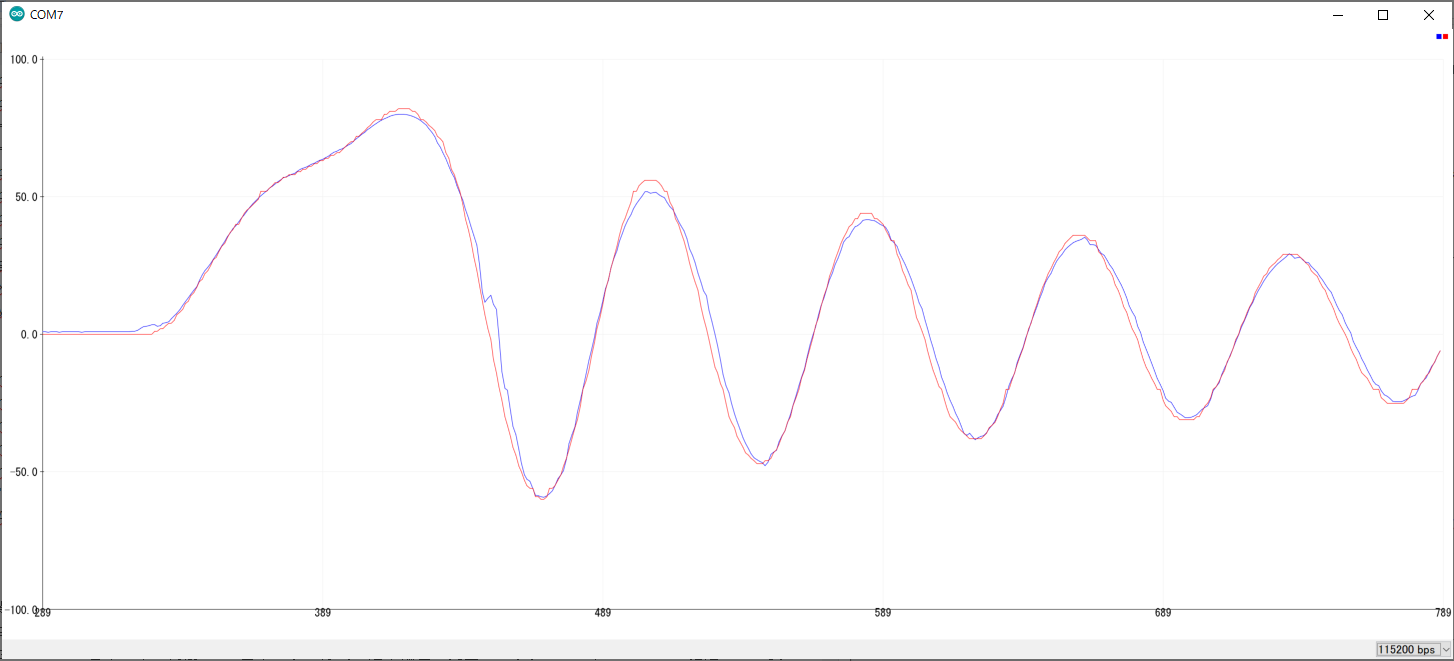
青:ジャイロのみから推定した 赤:3サンプル前の時刻のエンコーダーによる角度
かなり正確に推定できています。
手で激しく揺らすと
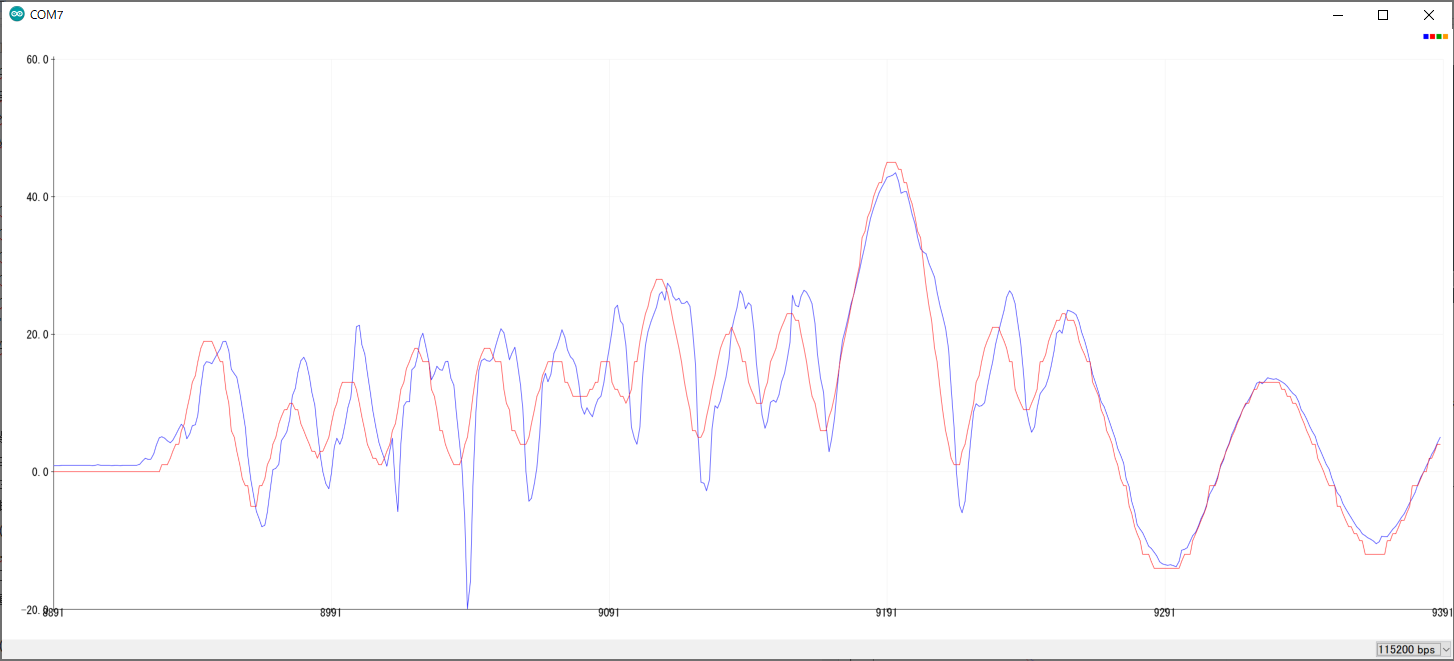
青:ジャイロのみから推定した 赤:3サンプル前の時刻のエンコーダーによる角度
結構ずれます。
原因として予測するのは
- 加速度センサ・ジャイロセンサー本体に付いているLPFによる遅れ
- 角加速度を計算する際に使った近似微分器による遅れ
ほかは思いつきませんでした。何か思いついたら教えてください。
間違っているところなど有れば。
重力のみと仮定して推定すると?
重力加速度のみによる場合は
\begin{bmatrix}
Accel_x'' \\
Accel_y''\\
\end{bmatrix} =
\begin{bmatrix}
C(\theta+\beta) & S(\theta+\beta) \\
-S(\theta+\beta) & C(\theta+\beta)\\
\end{bmatrix}
*
\begin{bmatrix}
g \\
0\\
\end{bmatrix} \\
=
\begin{bmatrix}
g*C(\theta+\beta) \\
-g*S(\theta+\beta) \\
\end{bmatrix} \\
より
\theta+\beta = Atan(-Acc_y''/Acc_x'')
より推定すると
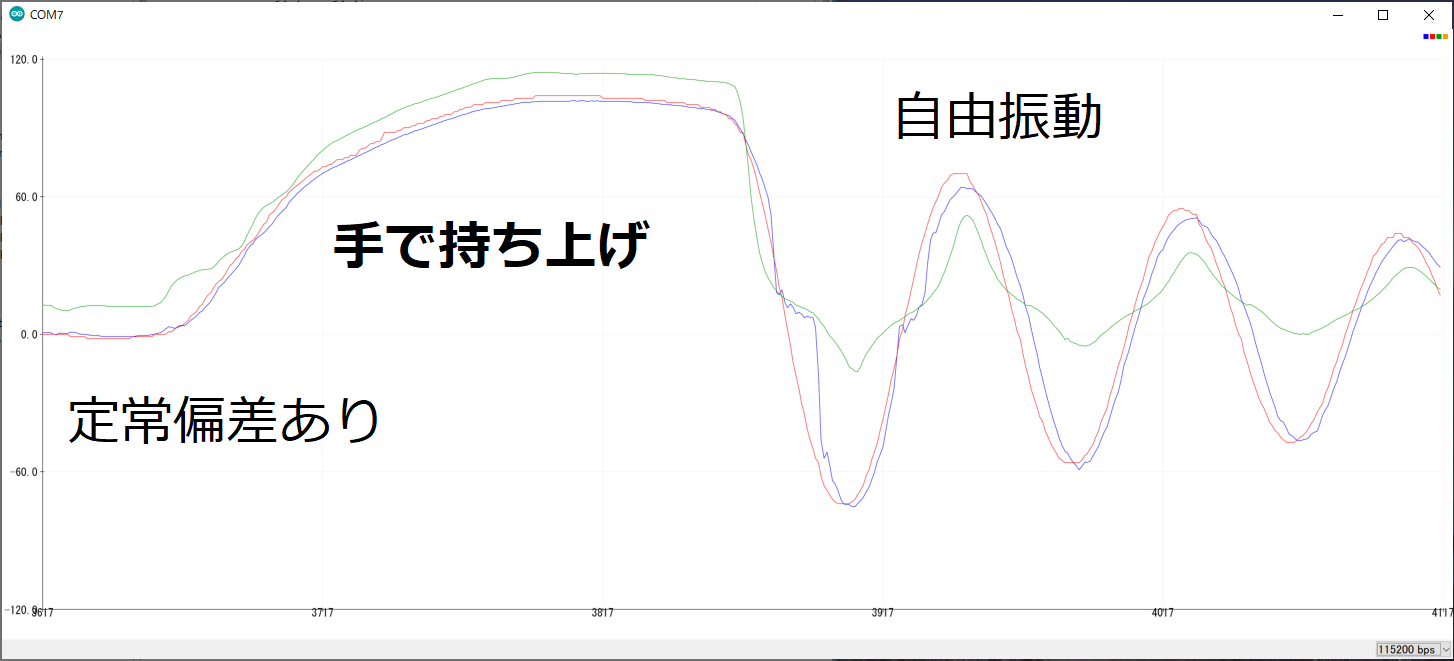
青:ジャイロのみから推定した 赤:3サンプル前の時刻のエンコーダーによる角度 緑:重力加速度のみによる推定
まず定常偏差が出るのと、自由振動で遠心力・角加速度由来の項が増加するとかするとかなり誤差がでかくなりました。
カルマンフィルタでの姿勢推定は重力のみで、オブザーバーを組みます。なぜならば回転半径Rが定まらず、知ることができないためです。おそらくですが、今回の場合によく使われるカルマンフィルタによる姿勢推定を組んでもあまり良い結果にならないと思っているのですが、どう思いますか?