2値分類モデルの予測値を確率として使用する際はCalibrationを行う必要があるらしいので調べました。

概要

Calibrationとは

広告のクリック率(CTR)予測など、2値分類モデルの予測値を確率として使用する際に必要な補正処理のこと。

どうしてCalibrationが必要なの？

機械学習モデルはデータから傾向を学習し予測を行いますが、2値分類モデルが学習するのは{0,1}の分類結果であって、分類確率ではないからです。
学習済みモデルに未知のデータを与えて予測すると0.0 ~ 1.0の間の小数が返ってきますが、これはあくまで予測結果であり、確率ではありません。
例えば、予測結果が0.1であるデータを集めて目的変数の平均をとっても0.1にならない場合があります。

また、学習データに含まれているのは分類結果であり、分類確率ではありません。
明示的に分類確率の学習データを集めるには、ユーザーにアンケートを取るなど工夫が必要です。

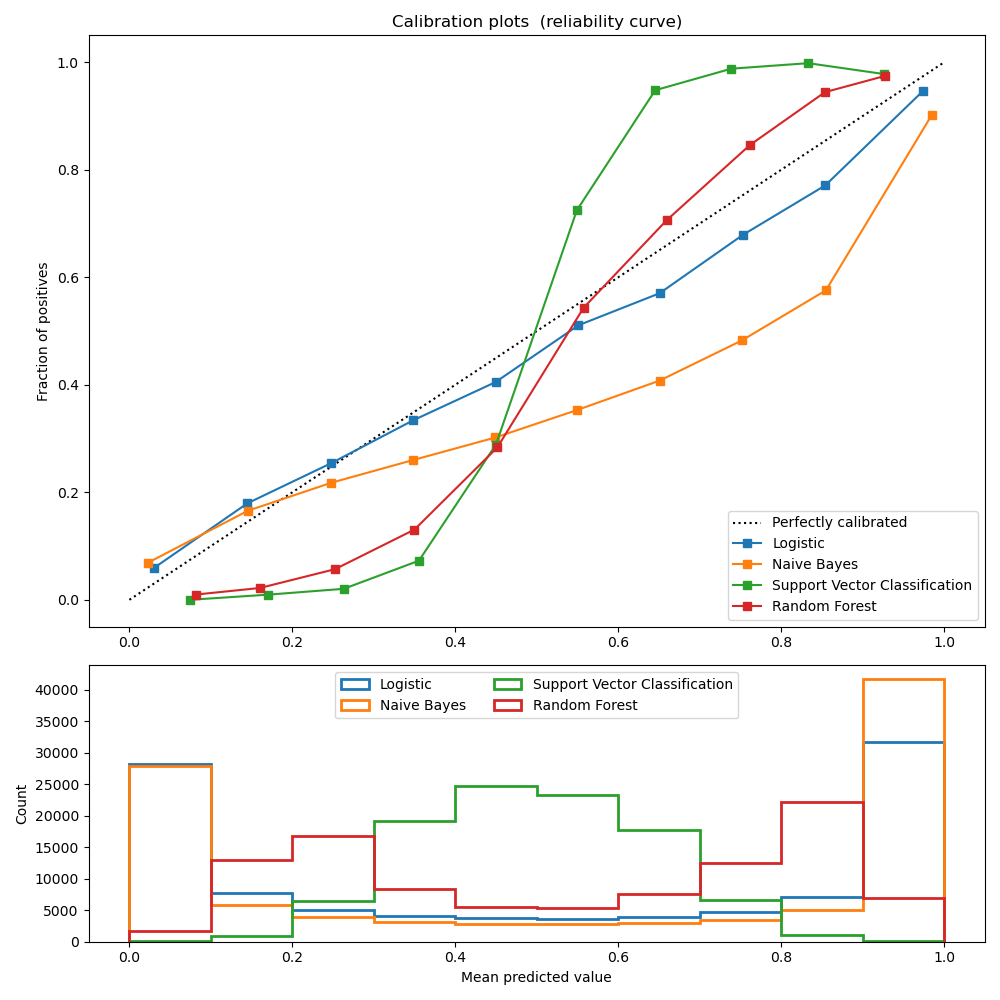
下の図は、主要な機械学習モデルの予測値と実績(確率)のシミュレーション結果を比較しています。
予測値=確率であれば全ての線は斜めの点線上に並ぶはずですが、実際は歪んでいます。
ただ、学習の際に確率を明示的に扱っているLogisticモデルはさほど歪んでいません。

(参考) "Probability Calibration"

どうやってCalibrationするの？

方法は2つあります。
1. Sigmoid Regressionを使う(Logisticモデルの歪みが少ない理由。詳細は省略)
2. Isotonic Regressionを使う(今回はこちらを採用)

今回は、データが1000サンプル以上ある場合に推奨され、またgoogleなど主要な会社で実際に使われているIsotonic Regressionを用います。

Isotonic Regressionって何？

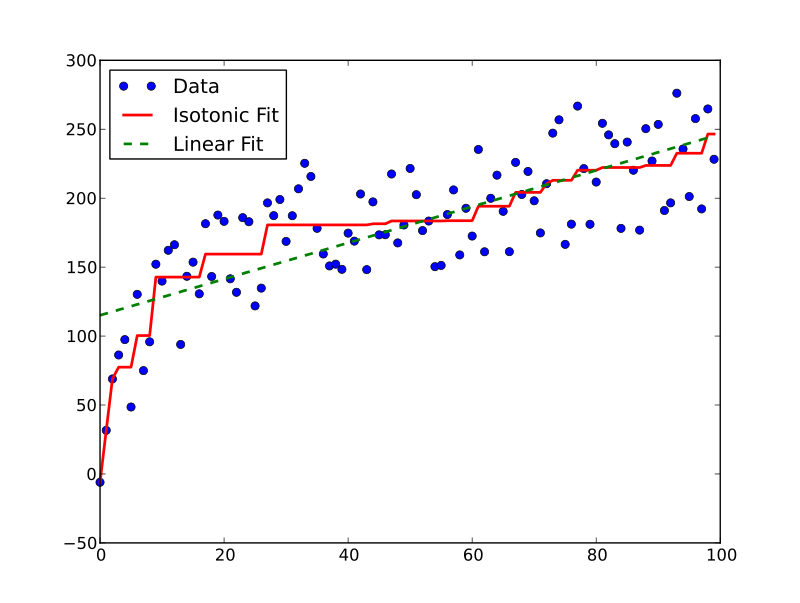
当てはめられた線がどこでも減少せず、観測値にできるだけ近くなるように、自由形式の線を一連の観測値に当てはめる手法

(wikipedia)

Isotonic Regressionは回帰分析の一つです。
入力が大きくなれば出力は常に大きくなる、単調増加する、という仮定の下、分類予測値を実績に基づく確率に補正します。

(wikipediaより)

上の例は目的変数が連続値の場合ですが、これが{0,1}の離散値の場合どのような挙動をするのか確かめます。

そこで、シミュレーションを行います。

シミュレーション

ライブラリのインストール

import numpy as np
import plotly.express as px
import pandas as pd

from sklearn.isotonic import IsotonicRegression

問題設定

今回は広告のクリック率予測について考えます。

真のCTRは平均0.5, 標準偏差0.3の正規分布から発生
サンプルサイズは1000
[0.0, 1.0]でclipping

ctr_prob = np.random.normal(loc=0.5, scale=0.3, size=1000).clip(0.0, 1.0)
ctr_prob.sort() # Isotonic Regressionを学習させるには、まず予測値をソートする必要がある
click = np.array([np.random.choice([0,1], size=1, p=[1-p, p]) for p in ctr_prob]).flatten()

px.scatter(
    pd.DataFrame({
    "x": ctr_prob,
    "y": click}),
    x="x",
    y="y",
    opacity=0.3,
    height=300, width=600  
)

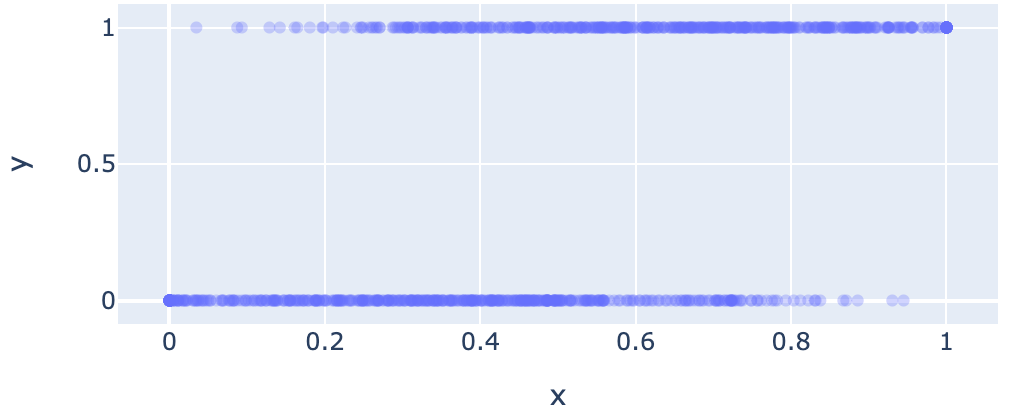
真のCTRに基づいてクリックを発生させると以下のようになります。

CTR予測値が歪んでいない場合

CTR予測値が真のCTRと一致している場合、Isotonic Regressionは(0,0), (1,1)を結んだ直線を学習します。

ir = IsotonicRegression(
    y_min=0.0,
    y_max=1.0,
    increasing=True,
    out_of_bounds="clip"
)

ctr_calibrated = ir.fit_transform(ctr_prob, click)

fig = px.line(pd.DataFrame({
    "ctr_prob": ctr_prob,
    "ctr_calibrated": ctr_calibrated
}), x="ctr_prob", y="ctr_calibrated")
fig.add_trace(
    px.scatter(
        pd.DataFrame({
            "ctr_prob": ctr_prob,
            "ctr_calibrated": click
        }),
        x="ctr_prob",
        y="ctr_calibrated",
        opacity=0.3,
    ).data[0]
)
fig.show()

CTR予測値と真のCTRは一致しています。
なので、calibrationをかけても値は特に変わりません。

CTR予測値が歪んでいる場合

適当にCTR予測値を歪ませます。

ctr_prob_distorted = np.log(1+ctr_prob*10)/2.5

px.line(
    pd.DataFrame({
      "ctr": ctr_prob,
      "ctr_prob_distorted": ctr_prob_distorted}),
    x="ctr",
    y="ctr_prob_distorted"
)

歪んだ予測値と広告配信実績を用いて、Isotonic Regressionを学習します。
歪んだCTR予測値をモデルが真のCTRに補正出来ているか確認します。

ctr_calibrated = ir.fit_transform(ctr_prob_distorted, click)

fig = px.line(pd.DataFrame({
    "ctr_prob_distorted": ctr_prob_distorted,
    "ctr_calibrated": ctr_calibrated
}), x="ctr_prob_distorted", y="ctr_calibrated")
fig.add_trace(
    px.scatter(
        pd.DataFrame({
            "ctr_prob_distorted": ctr_prob_distorted,
            "ctr_calibrated": click
        }),
        x="ctr_prob_distorted",
        y="ctr_calibrated",
        opacity=0.3,
    ).data[0]
)
fig.show()

Isotonic Regressionは先ほど歪ませた曲線と逆の形になりました。
例えば、ctr_prob_distorted=0.6の場合、ctr_calibrated=0.4となります。
これはctr_prob_distorted=0.6に歪ませる前の値であるctr=0.35に近い値です。
Isotonic Regressionが学習した曲線を通すと、歪んだCTR予測値が真のCTRに補正されることがわかります。

まとめ

分類を行う機械学習の予測値を確率として扱う場合、Calibrationが必要
Calibrationを行う手法の1つにIsotonic Regressionがある
2値分類タスクでシミュレーションを行ったところ、Isotonic Regressionは予測値を確率として用いる際の歪みを補正することが出来た

参考資料

(マイクロアド) "CTR予測における確率補正について"
(Alexandru Niculescu-Mizil, 2005) "Predicting Good Probabilities With Supervised Learning"
(Google, 2013) "Ad Click Prediction: a View from the Trenches"
(scikit-learn) "1.16. Probability calibration"

2値分類モデルの予測値を確率として使用する際にはCalibrationが必要

概要