注:この記事は、KawazAdventCalendar2014の12月16日ぶんです。
Kawaz(札幌ゲーム製作者コミュニティ)のサイト内に投稿した記事と同一のものです。
いきなり問題です
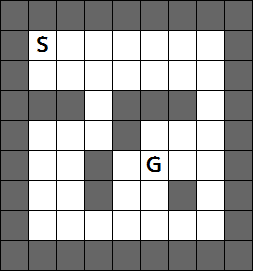
以下のようなマス目状のマップがある。このマップ上では、キャラクターは上下左右にのみ移動でき、かつ壁(黒いマス)にキャラクターは入れないものとする。
このマップにおいて、スタート(S)からゴール(G)に移動するキャラクターのAIを作ることを考える。
- 少し時間がかかってもいいので、SからGへの最短経路を求めるにはどうすればよいか。
- SからGへ試行錯誤しながら進む効率のよい方法はあるか。すなわち、試行錯誤ではあるものの、上下左右を等確率で選んで進むよりもゴールするまでの時間がかからないと見込まれる方法はあるか。
1. 最短経路を求める
これは以下の解き方で求められる。
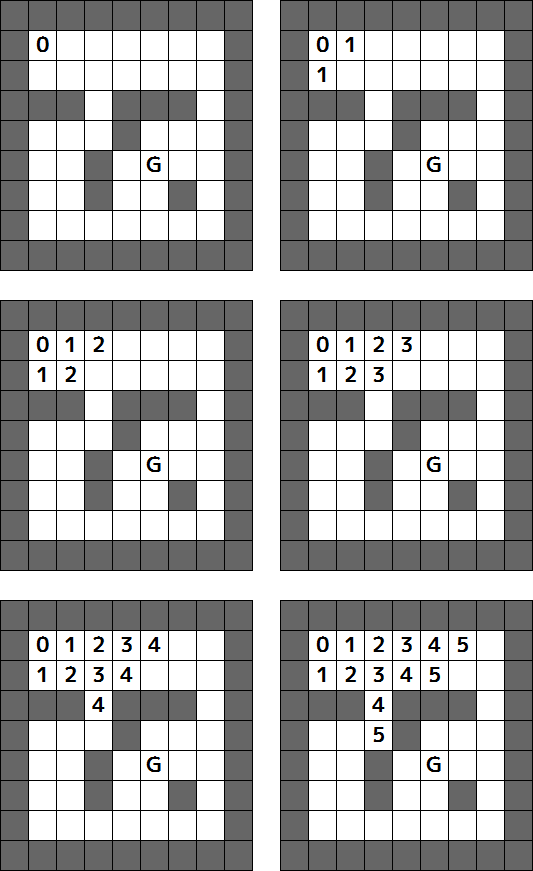
- Sのマスに「0」と書き込む。これは「Sから0回で移動できる場所」を意味する(これ以降も同様)。
- 以下のことを、全部のマスに数値が書き込まれるまで繰り返す。
- 「0」と書き込まれたマスから1回で移動できるマスすべてに「1」と書き込む。
- 「1」と書き込まれたマスから1回で移動できるマスすべて(ただし、すでに「0」や「1」が書き込まれているマスは除く)に「2」と書き込む。
- 「2」と書き込まれたマスから1回で移動できるマスすべて(ただし、すでに「0」や「1」や「2」が書き込まれているマスは除く)に「3」と書き込む。
- 以下同様
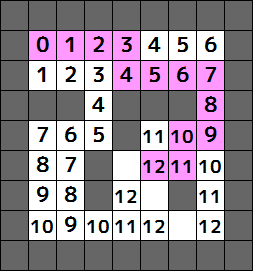
- 上記の過程において、どこからどこへ移動したことによって数字が書き込まれたかを記録しておく(同点があった場合はどれか一つを適当に選ぶ)。GのマスからSのマスへその移動方法を逆に辿れば最短経路が得られる。
このマップの場合、最終結果は以下のようになる。なお経路は一例であり、最後の「12」から1ずつ減るように0に戻れれば何でもよい。
これでうまくいくの?というのを疑問に感じる方もいるかもしれないが、これで問題ないのは、数字が書き込まれるのはSからの最短経路で移動してきた場合に限定される(あとで書こうとしてもすでに数字が書かれている)ためである。
この最短経路を求める手法は、より一般に「地点間の距離が1とは限らないようなマップ」の場合にも、少し工夫を加えることで適用することが可能であり、ダイクストラ法と呼ばれている。なお、計算時間は今回の問題だと地点数に比例する程度で済むものの、一般の場合には地点数の2乗に比例する時間となる。
余談:「マップ中のあらゆる2地点間の組み合わせに対する最短経路」を一挙に求める方法もあり、こちらはワーシャル-フロイド法と呼ばれている。計算時間は地点数の3乗に比例する。
2. 試行錯誤しながら進む
上下左右をランダムに選ぶより効率よくしたいということなので、
- 基本的にはゴール方向へ向かうようにするが、一定の確率で上下左右をランダムに選ぶ
というものが有力だろうか。その他細かい工夫もできるだろう。
Rubyで実装したコードはこちら。 https://gist.github.com/maraigue/809e6455bd192e1907fa
これを1000回動かして平均を取った結果はこちら。
| ゴール方向へ 向かう確率 |
移動回数の平均 (標準偏差) |
|---|---|
| 0.0 | 287.5 (228.9) |
| 0.1 | 199.4 (150.5) |
| 0.2 | 165.7 (109.6) |
| 0.3 | 154.2 (100.1) |
| 0.4 | 169.4 (117.5) |
| 0.5 | 210.3 (158.2) |
ゴール方向へ向かう確率が低くても高くても時間がかかる(移動回数が多くなる)ということがわかる。今回は試した5通りのうち、確率0.3が最適ということになった。
ただそれにしても、最短ルートが12回という中で154回も移動しないとゴールに着けないのではちょっと実用性に欠ける。完全ランダム(確率0.0)の287回に比べれば半分程度には減っているのだが。
現実的な対応としては、途中途中にチェックポイントを設けて、そこまで辿りつくようにするのを繰り返す、というところだろうか。このあたりは実際のゲームでルーチン作ったことがある方がいらっしゃったら教えていただきたい。
おわりに
ゲームAI大変です。でもうまく作れると楽しいので作ってみたいです。