ハイパークィーン問題とは
ずいぶん昔の科学雑誌『Quark』に載っていたパズルです。
チェスのクィーンは、縦横斜めすべての方向に動けます。将棋の飛車と角を合わせた動き方ができます。このパズルでは、さらに盤の左と右をくるっと回してくっつけてクィーンが動けると仮定します。同様に、上と下もくるっとまわしてくっつけ、クィーンが動けると仮定します。
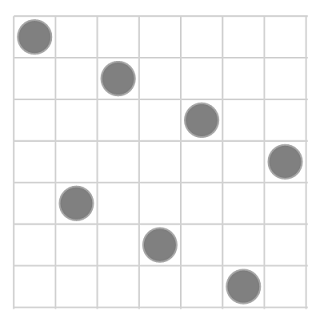
このとき、7×7の盤上に、お互いに利き筋にあたらないように7つのクィーンを配置してください。という問題です。
解のひとつを以下に示します。
どうやって解くか
1行目にひとつの駒を置いたら、次は、2行目に条件を満たすようにおき、次に、3行目も条件を満たすように駒を置く... とこれを7行目まで続けることで解を求めています。もちろん、途中で条件に合わない場合がでてきますので、その際はひとつ前に状態を戻し、さらに探索を続けることをやります。これを再帰処理を使って実装しています。いわゆるバックトラック法ですね。
Solverクラス(後述)でその処理をやっていますが、とても単純なものです。盤面に関する細かな処理をBoardクラス(後述)に委ねている効果ですね。
なお、鏡像や回転像も含めて求めています。
簡単なクラスの説明
主要なクラスは、Solverクラスと、Boardクラスです。
Solverクラスはパズルを解くクラスで、Boardクラスに駒を置きながらパズルを解いていきます。
Boardクラスは、7*7の盤面を表すクラスです。ただし、7×7の盤以外にも対応できるよう、コンストラクタで盤面の幅を渡してもらっています。5, 11などの奇数の整数を与えれば、ちゃんと答えを出してくれます。
このBoardクラスは、 他のパズル問題でも利用しているBoardBaseクラスから継承(後述)しています。
Boardクラス / Pieceクラス
Boardクラスは、HyperQueenパズルに特化した盤面クラスで、ルールに沿って駒を置けるかを判断したり、駒を置いたり取り除いたりする機能があります。
Pieceクラスは、その盤面に置く駒クラスを表しています。
using Puzzle;
using System;
using System.Collections.Generic;
using System.Text;
using System.Linq;
namespace HyperQueenApp {
public class Piece {
public static readonly Piece Empty = new Piece { Value = '.' };
public static readonly Piece Queen = new Piece { Value = 'Q' };
public char Value { get; set; }
public override string ToString() {
return Value.ToString();
}
}
class Board : BoardBase<Piece> {
private int _width;
public Board(int width) : base(width, width) {
_width = width;
foreach (var p in GetAllIndexes())
this[p] = Piece.Empty;
}
// コピーコンストラクタ
public Board(Board board) : base(board) {
}
// 駒を置く
public void Put(int place) {
this[place] = Piece.Queen;
}
// 指定した位置から駒を取り去る
public void Clear(int place) {
this[place] = Piece.Empty;
}
// 引数で与えた位置に駒を置けるか
public bool CanPut(int place) {
if (this[place] != Piece.Empty)
return false;
if (Courses(place).Any(p => this[p] == Piece.Queen))
return false;
return true;
}
// 与えられた位置の右、下、ななめ右下、ななめ左下の位置を
// それぞれぐるっと一回転するまで列挙する。
// ただし、与えられた位置は除く。
public IEnumerable<int> Courses(int index) {
var (x, y) = ToLocation(index);
return Virtical(x, 1)
.Concat(Horizontal(1, y))
.Concat(Oblique(x, y))
.Concat(BackOblique(x, y)).Where(p => p != index).Distinct();
}
// 左下がりの斜線の各位置を列挙する
public IEnumerable<int> Oblique(int x, int y) {
for (int i = 0; i < _width; i++) {
x += 1;
y -= 1;
if (x > _width)
x = 1;
if (y == 0)
y = _width;
yield return ToIndex(x, y);
}
}
// 右下がりの斜線の各位置を列挙する
public IEnumerable<int> BackOblique(int x, int y) {
for (int i = 0; i < _width; i++) {
x += 1;
y += 1;
if (x > _width)
x = 1;
if (y > _width)
y = 1;
yield return ToIndex(x, y);
}
}
}
}
Solverクラス
HyperQueenを解くクラス。盤面操作の面倒なところはBoardクラスに隠蔽されているので、
Solveerクラスはとてもすっきりしたものになっています。
using System;
using System.Collections.Generic;
using System.Text;
using System.Linq;
namespace HyperQueenApp {
class Solver {
public IEnumerable<Board> Solve(Board board) {
return SolveInner(board, 1);
}
// y行よりも下に置く駒を求める - 鏡像、回転を除くことは考慮していない
private IEnumerable<Board> SolveInner(Board board, int y) {
if (y > board.YSize) {
yield return new Board(board);
yield break;
}
foreach (int pos in board.Horizontal(1, y)) {
if (board.CanPut(pos)) {
board.Put(pos);
foreach (var b in SolveInner(board, y + 1))
yield return b;
board.Clear(pos);
}
}
}
}
}
Programクラス
using System;
namespace HyperQueenApp {
class Program {
static void Main(string[] args) {
var solver = new Solver();
var board = new Board(7);
foreach (var r in solver.Solve(board)) {
Print(board);
}
}
static void Print(Board board) {
for (int y = 1; y <= board.YSize; y++) {
for (int x = 1; x <= board.XSize; x++) {
var p = board[x, y];
char c = (p == Piece.Queen) ? 'Q' : '.';
Console.Write(c + " ");
}
Console.WriteLine();
}
Console.WriteLine();
}
}
}
実行結果
実行結果です。ちょっと長いです。
Q . . . . . .
. . Q . . . .
. . . . Q . .
. . . . . . Q
. Q . . . . .
. . . Q . . .
. . . . . Q .
Q . . . . . .
. . . Q . . .
. . . . . . Q
. . Q . . . .
. . . . . Q .
. Q . . . . .
. . . . Q . .
Q . . . . . .
. . . . Q . .
. Q . . . . .
. . . . . Q .
. . Q . . . .
. . . . . . Q
. . . Q . . .
Q . . . . . .
. . . . . Q .
. . . Q . . .
. Q . . . . .
. . . . . . Q
. . . . Q . .
. . Q . . . .
. Q . . . . .
. . . Q . . .
. . . . . Q .
Q . . . . . .
. . Q . . . .
. . . . Q . .
. . . . . . Q
. Q . . . . .
. . . . Q . .
Q . . . . . .
. . . Q . . .
. . . . . . Q
. . Q . . . .
. . . . . Q .
. Q . . . . .
. . . . . Q .
. . Q . . . .
. . . . . . Q
. . . Q . . .
Q . . . . . .
. . . . Q . .
. Q . . . . .
. . . . . . Q
. . . . Q . .
. . Q . . . .
Q . . . . . .
. . . . . Q .
. . . Q . . .
. . Q . . . .
Q . . . . . .
. . . . . Q .
. . . Q . . .
. Q . . . . .
. . . . . . Q
. . . . Q . .
. . Q . . . .
. . . . Q . .
. . . . . . Q
. Q . . . . .
. . . Q . . .
. . . . . Q .
Q . . . . . .
. . Q . . . .
. . . . . Q .
. Q . . . . .
. . . . Q . .
Q . . . . . .
. . . Q . . .
. . . . . . Q
. . Q . . . .
. . . . . . Q
. . . Q . . .
Q . . . . . .
. . . . Q . .
. Q . . . . .
. . . . . Q .
. . . Q . . .
Q . . . . . .
. . . . Q . .
. Q . . . . .
. . . . . Q .
. . Q . . . .
. . . . . . Q
. . . Q . . .
. Q . . . . .
. . . . . . Q
. . . . Q . .
. . Q . . . .
Q . . . . . .
. . . . . Q .
. . . Q . . .
. . . . . Q .
Q . . . . . .
. . Q . . . .
. . . . Q . .
. . . . . . Q
. Q . . . . .
. . . Q . . .
. . . . . . Q
. . Q . . . .
. . . . . Q .
. Q . . . . .
. . . . Q . .
Q . . . . . .
. . . . Q . .
Q . . . . . .
. . . Q . . .
. . . . . . Q
. . Q . . . .
. . . . . Q .
. Q . . . . .
. . . . Q . .
. Q . . . . .
. . . . . Q .
. . Q . . . .
. . . . . . Q
. . . Q . . .
Q . . . . . .
. . . . Q . .
. . Q . . . .
Q . . . . . .
. . . . . Q .
. . . Q . . .
. Q . . . . .
. . . . . . Q
. . . . Q . .
. . . . . . Q
. Q . . . . .
. . . Q . . .
. . . . . Q .
Q . . . . . .
. . Q . . . .
. . . . . Q .
Q . . . . . .
. . Q . . . .
. . . . Q . .
. . . . . . Q
. Q . . . . .
. . . Q . . .
. . . . . Q .
. Q . . . . .
. . . . Q . .
Q . . . . . .
. . . Q . . .
. . . . . . Q
. . Q . . . .
. . . . . Q .
. . Q . . . .
. . . . . . Q
. . . Q . . .
Q . . . . . .
. . . . Q . .
. Q . . . . .
. . . . . Q .
. . . Q . . .
. Q . . . . .
. . . . . . Q
. . . . Q . .
. . Q . . . .
Q . . . . . .
. . . . . . Q
. Q . . . . .
. . . Q . . .
. . . . . Q .
Q . . . . . .
. . Q . . . .
. . . . Q . .
. . . . . . Q
. . Q . . . .
. . . . . Q .
. Q . . . . .
. . . . Q . .
Q . . . . . .
. . . Q . . .
. . . . . . Q
. . . Q . . .
Q . . . . . .
. . . . Q . .
. Q . . . . .
. . . . . Q .
. . Q . . . .
. . . . . . Q
. . . . Q . .
. . Q . . . .
Q . . . . . .
. . . . . Q .
. . . Q . . .
. Q . . . . .
BoardBaseクラス
このBoardBaseクラスは、「騎士巡回問題」「ナイト(騎士)の最適配置問題」などで利用したものと同じものです。
前述のBoardクラスの基底クラスです。X × Y の盤面を表し、基本的な操作を定義しています。これは似たようなパズルでも再利用できるような汎用的な機能に絞っています。このBoardBaseクラスは、コンソールアプリに依存しない作りにしています。UWP、WinFormsでもそのまま使えると思います。
このBoardBaseを継承して、当パズル専用のBoardクラスを定義します。
内部では1次元配列を使っていますが、インデクサを定義して、1次元配列、2次元配列としても扱えるようにしています。
ただし、すべてのメソッドで1次元対応と2次元対応のものを用意するのは面倒なので、どちらか一方にしています。まあこれは好み以外の何物でもありません。
1次元のインデックスによるアクセスができるようにしている理由は、一重ループで処理が書けるので、コードが簡潔になるからです。LINQのコードも書きやすくなります。
2次元配列として見た場合の、X座標、Y座標は、0 からではなく、1から始まります。
つまり、board[1,1] は、いちばん左上を示し、8×8の盤ならば、board[8,8]が右下を示すことになります。
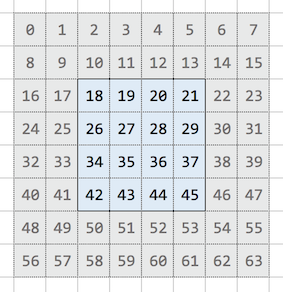
なお、盤の周りには番兵用の領域を用意しています。これにより範囲外かどうかの判断を簡単に出来るようにしています。チェスのナイト(騎士)の動きにも対応できるよう、番兵は二重にしています。
上の図は 4×4の盤を表していますが、グレー部分が番兵が置いてある盤の周囲で、水色部分が実際の盤です。
盤面上の数値は、1次元配列のインデックスを表しています。
なお、派生クラスや派生クラスを利用するクラスが、この番兵の存在に依存しないように、ToDirectionという関数を定義し、X方向、Y方向のペアで表す移動方向(ベクトル)をインデックスで表す方向に変換するようにしています。
BoardBaseクラスはジェネリッククラスにしていて、そのパラメータの型は、盤面上に置けるクラスの型です。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Puzzle {
// 汎用の盤面クラス
// Tは、盤面に置けるオブジェクトの型。参照型でnew()ができれば何でも良い。
public abstract class BoardBase<T> where T : class, new() {
private T[] _pieces;
// 盤の行数(縦方向)
public int YSize { get; private set; }
// 盤のカラム数(横方向)
public int XSize { get; private set; }
// コンストラクタ
public BoardBase(int xsize, int ysize) {
this.YSize = ysize;
this.XSize = xsize;
_pieces = new T[(xsize + 2) * (ysize + 2)];
// 盤データの初期化 - 盤の周りはnull(番兵)をセットしておく
ClearAll();
}
// コピー用コンストラクタ
public BoardBase(BoardBase<T> board) {
XSize = board.XSize;
YSize = board.YSize;
this._pieces = board._pieces.ToArray();
}
// 番兵も含めたボード配列の長さ
public int BoardLength {
get { return _pieces.Length; }
}
// インデクサ (x,y)の位置の要素へアクセスする
public T this[int index] {
get { return _pieces[index]; }
set { _pieces[index] = value; }
}
// インデクサ (x,y)の位置の要素へアクセスする
public T this[int x, int y] {
get { return this[ToIndex(x, y)]; }
set { this[ToIndex(x, y)] = value; }
}
// Location から _coinのIndexを求める
public int ToIndex(int x, int y) => x + y * (XSize + 2);
// IndexからLocationを求める (ToIndexの逆演算)
public (int, int) ToLocation(int index) => (index % (XSize + 2), index / (XSize + 2));
// 本来のボード上の位置(index)かどうかを調べる
public virtual bool IsOnBoard(int index) {
if (0 <= index && index < BoardLength)
return this[index] != null;
return false;
}
// 全てのPieceをクリアする
public virtual void ClearAll() {
for (int index = 0; index < BoardLength; index++)
this[index] = null; // 番兵
foreach (var index in GetAllIndexes())
this[index] = new T(); // 初期値
}
// 盤上のすべての位置(index)を列挙する
public virtual IEnumerable<int> GetAllIndexes() {
for (int y = 1; y <= this.YSize; y++) {
for (int x = 1; x <= this.XSize; x++) {
yield return ToIndex(x, y);
}
}
}
// (x,y)からdirection方向の位置を列挙する (x,y)含む
public virtual IEnumerable<int> EnumerateIndexes(int x, int y, int direction) {
for (int index = ToIndex(x, y); IsOnBoard(index) && this[index] != null; index += direction)
yield return index;
}
// (x,y)から右(水平)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> Horizontal(int x, int y)
=> EnumerateIndexes(x, y, 1);
// (x,y)から下(垂直)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> Virtical(int x, int y)
=> EnumerateIndexes(x, y, this.XSize + 2);
// (x,y)から右斜め下(45度)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> SlantR(int x, int y)
=> EnumerateIndexes(x, y, this.XSize + 2 + 1);
// (x,y)から左斜め下(45度)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> SlantL(int x, int y)
=> EnumerateIndexes(x, y, this.XSize + 2 - 1);
}
}
この記事は、Gushwell's C# Programming Pageで公開したものを大幅に加筆・修正したものです。