EM法による混合正規分布の最尤推定を理解したい

はじめに

• EM法の考え方のメモです。
• 参考文献 人工知能の学習理論 渡辺澄夫
• 参考文献 EMアルゴリズム徹底解説@kenmatsu4

問題設定

• データ$X[x_n]$について混合正規分布を仮定する。
• 尤度$p(X|\pi,\mu,\Sigma)$を最大化するパラメータ$\pi,\mu,\Sigma$を推定する。

\begin{align}
p(x_n|\pi,\mu,\Sigma)&=\sum_{k=1}^K \pi_k N(x_n|\mu_k,\Sigma_k)
\quad(-\infty<x<\infty)\\
p(X|\pi,\mu,\Sigma)&=\prod_{n=1}^N p(x_n|\pi,\mu,\Sigma)
=\prod_{n=1}^N \left(\sum_{k=1}^K \pi_k N(x_n|\mu_k,\Sigma_k)\right)\\
\end{align}

隠れ変数の導入

• 計算手順を導出するために隠れ変数$z$を導入する。
• $K=3$の場合は、$(z_1,z_2,z_3)\in[(1,0,0),(0,1,0),(0,0,1)]$となる。

\begin{align}
p(x,z|\pi,\mu,\Sigma)&=\prod_{k=1}^K (\pi_k N(x|\mu_k,\Sigma_k))^{z_{k}}\\
p(X,Z|\pi,\mu,\Sigma)&=\prod_{n=1}^N \prod_{k=1}^K (\pi_k N(x_n|\mu_k,\Sigma_k))^{z_{nk}}\\
p(X|\pi,\mu,\Sigma)&=\sum^Z p(X,Z|\pi,\mu,\Sigma)\quad (|Z|=K^N)
\end{align}

EM法の考え方

(1) 初期パラメータ$w_1$に対応する同時分布$p(X,Z|w_1)$から$Z$の分布$p(Z|X,w_1)$を求める。
(2) $\log p(X,Z|w)$の期待値$\sum^Z p(Z|X,w_1) \log p(X,Z|w)$を最大化するパラメータ$w_2$を求める。
(3) $w_2$を$w_1$に代入してこれを繰り返す。

具体的な計算手順

(1) Eステップ$(\pi_k,\mu_k,\Sigma_k\rightarrow r_{nk})$
$Z[z_{nk}]$は離散分布なのでそれぞれの確率値を計算する。

\begin{align}
E[z_{nk}]&=\frac{\pi_kN(x_n|\mu_k,\Sigma_k)}
{\sum_{k=1}^K \pi_kN(x_n|\mu_k,\Sigma_k)}=r_{nk}\\
p(Z|X,w_1)&=\prod_{n=1}^N \prod_{k=1}^K r_{nk}^{z_{nk}}
\end{align}

(2) Mステップ$(r_{nk}\rightarrow \pi_k,\mu_k,\Sigma_k)$
期待値を計算して最大化する。結果のみ記す。

\begin{align}
\sum^Z p(Z|X,w_1) \log p(X,Z|w)&=\sum_{n=1}^N\sum_{k=1}^K r_{nk}
\log\left(\pi_k N(x_n|\mu_k,\Sigma_k)\right)
\end{align}

\begin{align}
\pi_k&=\frac{N_k}{N},\quad N_k=\sum_{n=1}^N r_{nk}\\
\mu_k&=\frac{1}{N_k}\sum_{n=1}^N r_{nk}x_n\\
\Sigma_k&=\frac{1}{N_k}\sum_{n=1}^N r_{nk}(x_n-\mu_k)(x_n-\mu_k)^t
\end{align}

対数尤度が単調非減少となる理由

• $\log p(X,Z|w_2)$の期待値を$G(w_1,w_2)$とする。EM法ではこれを$w_2$について最大化する。
• $G(w_1,w_2)$に基づいて$G^* (w_1,w_2)$を定義する。これは対数尤度からKL情報量を引いた値となる。
• $G^* (w_1,w_2)$と$G(w_1,w_2)$の差異は$w_1$に関する項のみなので、$w_2 $に関する最大化条件は、$G^* (w_1,w_2)$と$G(w_1,w_2)$で一致する。

\begin{align}
G(w_1,w_2)&=\sum^Z p(Z|X,w_1)\log p(X,Z|w_2)\\
G^*(w_1,w_2)&=G(w_1,w_2)-\sum^Z p(Z|X,w_1)\log p(Z|X,w_1)\\
&=\sum^Z p(Z|X,w_1)\left[\log p(X,Z|w_2)-\log p(Z|X,w_1)\right]\\
&=\sum^Z p(Z|X,w_1)\left[\log p(X|w_2)+\log p(Z|X,w_2)-\log p(Z|X,w_1)\right]\\
&=\log p(X|w_2)-\sum^Z p(Z|X,w_1)\frac{\log p(Z|X,w_1)}{\log p(Z|X,w_2)}
\end{align}

• $G^* (w_1,w_2)$の最大化条件とKL情報量が常にゼロ以上であることから、次の不等式が成り立つ。

\begin{align}
G^* (w_1,w_1) \le G^* (w_1,w_2) \le \log p(X|w_2)
\end{align}

• 従って次の不等式が成り立つ。

\begin{align}
\log p(X|w_1) \le G^* (w_1,w_2) \le \log p(X|w_2)
\end{align}

変分下限を用いた説明

• $G^*(w_1,w_2)$は変分下限に相当している。
• 対数周辺尤度$\log p(X|w)$を変分下限$L(q,w)$とKL情報量の和に分解する。
• ここで$q(Z)$は$Z$の任意の確率分布とする。
• 変分下限の形式はKL情報量と似ているが、$p(X,Z|w)$は$Z$で和を取っても1にはならない。

\begin{align}
\log p(X|w)&=\sum^Z q(Z)\log p(X|w)\\
&=\sum^Z q(Z)\log\frac{p(X,Z|w)}{p(Z|X,w)}\frac{q(Z)}{q(Z)}\\
&=\sum^Z q(Z)\log\frac{p(X,Z|w)}{q(Z)}+\sum^Z q(Z)\log\frac{q(Z)}{p(Z|X,w)}\\
\log p(X|w)&=L(q,w)+\mathrm{KL}(q(Z)\parallel p(Z|X,w))
\end{align}

• 初期パラメータ$w_1$に対して、$q_1(Z)=p(Z|X,w_1)$とする。
• EM法における$\log p(X,Z|w)$の期待値の最大化条件は、変分下限$L(q_1,w)$の最大化条件と一致する。

\begin{align}
\log p(X|w_1)&=L(q_1,w_1)\quad (q_1(Z)=p(Z|X,w_1))\\
L(q_1,w_1)&\le L(q_1,w_2)\quad (max\ at\ w_2)\\
\log p(X|w_2)&=L(q_1,w_2)+\mathrm{KL}(q_1(Z)\parallel p(Z|X,w_2))\\
&=L(q_2,w_2)\quad (q_2(Z)=p(Z|X,w_2))
\end{align}

• 従って次の不等式が成り立つ。

\begin{align}
\log p(X|w_1) &\le L(q_1,w_2) \le \log p(X|w_2)\\
L(q_1,w_1) &\le L(q_1,w_2) \le L(q_2,w_2)
\end{align}

• EM法は、対数周辺尤度を最大化するために、変分下限を順次最大化していく方法。

Rプログラムと実行結果

# Multivariate Normal Distribution
my_mvrnorm = function(n, mm, sig){
  ar = t(chol(sig))
  m = length(mm)
  y = ar %*% matrix(rnorm(n*m),nrow=m,ncol=n) + mm
  t(y)
}
my_mvdnorm = function(xn, mm, sig){
  sig_ = solve(sig)
  xm = t(xn) - mm
  ss = colSums(xm * (sig_ %*% xm))
  f1 = log(det(sig)) + length(mm)*log(2*pi)
  f2 = (f1 + ss) * 0.5
  exp(-f2)
}

# Normalizing constant of Dirichlet distribution
my_log_C = function(a){
  lgamma(sum(a))-sum(lgamma(a))
}
# Normalizing constant of Wishart distribution
my_log_B = function(W,nu){
  d = nrow(W)
  -nu/2*log(det(W)) - nu*d/2*log(2) - d*(d-1)/4*log(pi) - sum(lgamma((nu+1-1:d)/2))
}

my_plot_ellipse = function(mm, sig){
  ar = t(chol(sig))
  theta = seq(-pi, pi, length=100)
  y = matrix(c(cos(theta),sin(theta)),nrow=2,ncol=100,byrow=T)
  x = ar %*% y + mm
  polygon(x[1,], x[2,])
}

# Data generation
N = 100 # number of points
D = 2  # dimension
K = 3  # number of cluster
set.seed(10)

rt = (function(){
  kr = c(1,2,1); kr = kr/sum(kr)  # allocation ratio
  kd = c(0.3,0.5,1)/2  # diagonal term of variance
  mu = matrix(c(0,0,0,2,2,1),nrow=K,ncol=D,byrow=T) # mean
  sigma = lapply(1:K,function(k){ # variance-covariance matrix
    diag(kd[k],nrow=D,ncol=D)
  })
  nk = as.integer(kr*N+0.5)
  nk[1] = N - sum(nk[-1])
  xn = NULL # data points
  gn = NULL # cluster id
  for(k in 1:K){
    xn = rbind(xn,my_mvrnorm(nk[k],mu[k,],sigma[[k]]))
    gn = c(gn,rep(k,nk[k]))
  }
  list(xn=xn,gn=gn,mu=mu,sigma=sigma)
})()
xn = rt$xn

cols = rainbow(K)
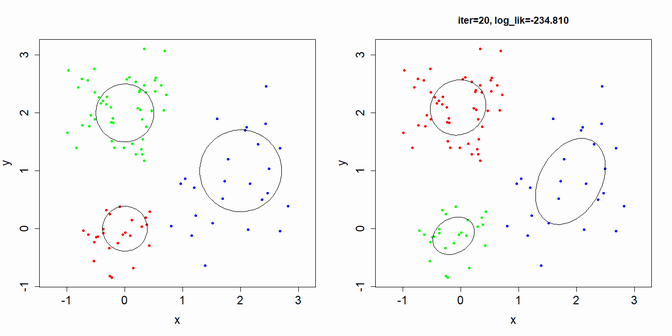
plot(rt$xn,xlab="x",ylab="y",type="p",pch=20,col=cols[rt$gn],asp=1,cex.axis=1.5,cex.lab=1.5)
for(k in 1:K){
  my_plot_ellipse(rt$mu[k,], rt$sigma[[k]])
}

# Expectation Maximization Algorithm

N = nrow(xn)
D = ncol(xn)
K = 3
cols = rainbow(K)

# Initial parameter
set.seed(10)
pik = rep(1/K,K)
muk = matrix(runif(D*K,min=0,max=2),nrow=K,ncol=D)
sgk = rep(list(diag(D)),K)
log_lik = numeric()

for(iter in 1:20){
  # E step
  rho = sapply(1:K,function(k){pik[k]*my_mvdnorm(xn,muk[k,],sgk[[k]])})
  rho_sum = rowSums(rho)
  rnk = rho / rho_sum
  (L = sum(log(rho_sum))) # Log Likelihood
  log_lik[iter] = L

  # M step
  nk = colSums(rnk)
  pik = nk / sum(nk)
  muk = (t(rnk) %*% xn) / nk
  sgk = lapply(1:K,function(k){
    s1 = t(t(xn) - muk[k,])
    s2 = s1 * rnk[,k]
    (t(s2) %*% s1) / nk[k]
  })

  msg = sprintf("iter=%d, log_lik=%.3f",iter,L)
  gnk = apply(rnk,1,which.max)
  plot(xn,main=msg,xlab="x",ylab="y",type="p",pch=20,col=cols[gnk],asp=1,cex.axis=1.5,cex.lab=1.5)
  for(k in 1:K){
    my_plot_ellipse(muk[k,], sgk[[k]])
  }
  Sys.sleep(1)
}
data.frame(log_lik,diff=diff(c(NA,log_lik)))

     log_lik         diff
1  -311.7150           NA
2  -284.3647 2.735032e+01
3  -280.8348 3.529909e+00
4  -276.9655 3.869326e+00
5  -273.0891 3.876357e+00
6  -269.3396 3.749509e+00
7  -265.7025 3.637110e+00
8  -261.5865 4.115985e+00
9  -255.4391 6.147431e+00
10 -246.6888 8.750279e+00
11 -239.7364 6.952428e+00
12 -236.5408 3.195545e+00
13 -235.1414 1.399410e+00
14 -234.9248 2.166463e-01
15 -234.8515 7.323482e-02
16 -234.8242 2.730015e-02
17 -234.8146 9.627078e-03
18 -234.8113 3.311071e-03
19 -234.8102 1.124729e-03
20 -234.8098 3.793261e-04