Rで2変数ガウス分布を因子分解して変分近似

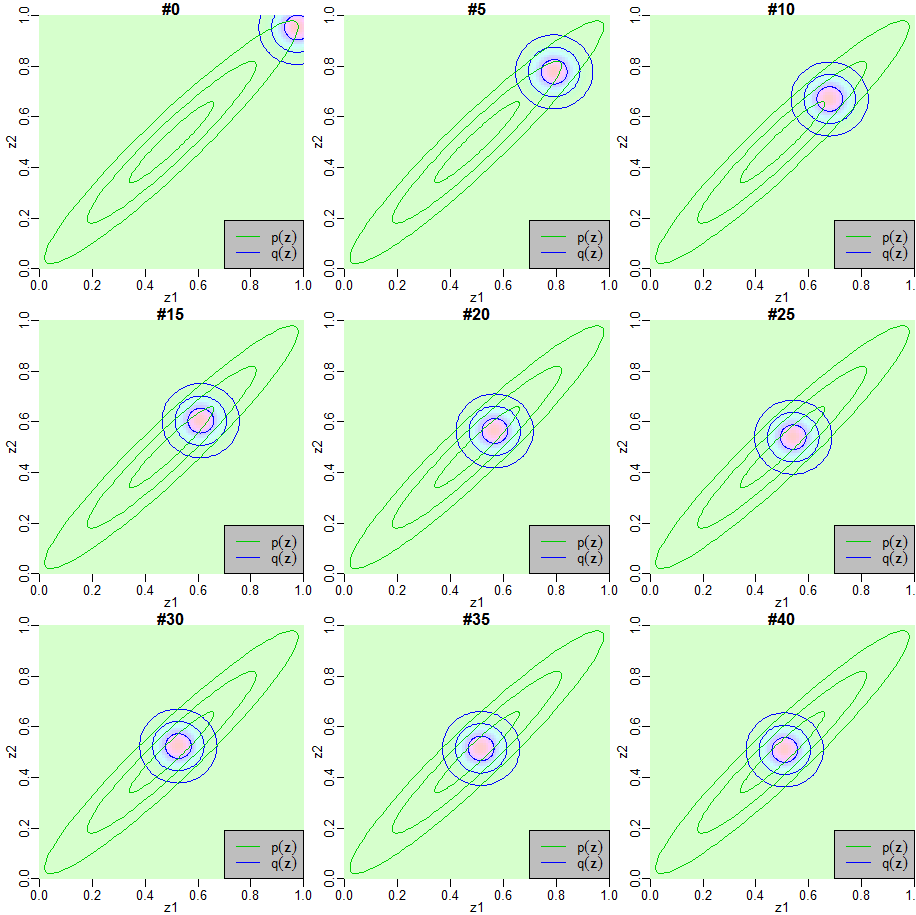
PRML図10.2(a)と同様に、相関のある2つの変数$\mathbf{z}=(z_1,z_2)^T$についてのガウス分布

p(\mathbf{z})=N(\mathbf{z}|\mathbf{\mu},\mathbf{\Lambda}^{-1}),\ 
\mathbf{\mu}=\left(\begin{array}{c}
\mu_1 \\
\mu_2
\end{array}\right),\ 
\mathbf{\Lambda}=\left(\begin{array}{cc}
\Lambda_{11} & \Lambda_{12} \\
\Lambda_{12} & \Lambda_{22}
\end{array}\right)

を、分解したガウス分布$q(\mathbf{z})=q_1(z_1)q_2(z_2)$で変分近似します。そして、元のガウス分布と近似した分布それぞれについて、標準偏差の1,2,3倍の等高線を描画します。

まず、変分近似により最適な因子$q_1^\star(z_1), q_2^\star(z_2)$を求めると、以下のようになります。

q_1^\star(z_1)=N(z_1|m_1,\Lambda_{11}^{-1}),\ 
m_1=\mu_1-\Lambda_{11}^{-1}\Lambda_{12}(E_{z_2}[z_2]-\mu_2) \\
q_2^\star(z_2)=N(z_2|m_2,\Lambda_{22}^{-1}),\ 
m_2=\mu_2-\Lambda_{22}^{-1}\Lambda_{12}(E_{z_1}[z_1]-\mu_1)

$E_{z_1}[z_1], E_{z_2}[z_2]$は、ガウス分布の平均パラメータで与えられるので、以下のようになります。

E_{z_1}[z_1]=\mu_1-\Lambda_{11}^{-1}\Lambda_{12}(E_{z_2}[z_2]-\mu_2) \\
E_{z_2}[z_2]=\mu_2-\Lambda_{22}^{-1}\Lambda_{12}(E_{z_1}[z_1]-\mu_1)

この場合、PRMLに記載の通り、$q_1^\star(z_1), q_2^\star(z_2)$は解析的に求まりますが、ここでは適当な初期値から初めて、$q_1^\star(z_1)$と$q_2^\star(z_2)$を交互に更新していく手法で$q(\mathbf{z})$を求めています。

library(plotrix)
frame()
set.seed(0)
par(mfrow=c(3, 3))
par(mar=c(2.3, 2.5, 1, 0.1))
par(mgp=c(1.3, .5, 0))
colors <- hsv(seq(0.3, 1, 0.01), 0.2, 1)
z1range <- c(0, 1)
z2range <- c(0, 1)
z1 <- seq(z1range[1], z1range[2], 0.01)
z2 <- seq(z2range[1], z2range[2], 0.01)

# 真のガウス分布のパラメータ
mu <- c(.5, .5)
L11 <- 420
L12 <- -400
L22 <- 420
L <- matrix(c(L11, L12, L12, L22), 2)
sigma <- solve(L)

# E[z2]を適当な初期値に設定する
Ez2 <- 1

for (iteration in 0:40) {
    # 因子 q1(z1)=N(z1|m1,L11^-1) を求める
    m1 <- mu[1] - L12 / L11 * (Ez2 - mu[2])
    Ez1 <- m1  # E[N(z|u,s^2)] = u

    # 因子 q2(z2)=N(z2|m2,L22^-1) を求める
    m2 <- mu[2] - L12 / L22 * (Ez1 - mu[1])
    Ez2 <- m2  # E[N(z|u,s^2)] = u

    cat(paste("m1=", m1, " m2=", m2, "\n"))
    if (iteration %% 5 == 0) {
        # 近似した分布を描画する
        q <- outer(z1, z2, function(z1, z2) {
            dnorm(z1, m1, sqrt(L11 ^ -1)) * dnorm(z2, m2, sqrt(L22 ^ -1))
            });
        image(z1, z2, q, xlim=z1range, ylim=z2range, col=colors)
        for (i in 1:3) {
            draw.ellipse(m1, m2, sqrt(L11 ^ -1) * i, sqrt(L22 ^ -1) * i, 0,
                border=4)
        }

        # 真の分布を描画する
        e <- eigen(sigma)
        for (i in 1:3) {
            draw.ellipse(mu[1], mu[2], sqrt(e$values[1]) * i, sqrt(e$values[2]) * i,
                atan2(e$vectors[2, 1], e$vectors[1, 1]) / pi * 180,
                border=3)
        }

        legend("bottomright", c(
            expression(p(bold(z))), 
            expression(q(bold(z)))
            ), col=c(3, 4), lty=1, bg="gray")
        title(paste0("#", iteration))
    }

}