2章 パーセプトロン
- パーセプトロンとは、アルゴリズムの名称であり、ニューラルネットワークの起源となるものでもある。
- 複数の信号を入力として受け取り、一つの信号を出力
2つの入力を受け取るパーセプトロンの一例を下記に示す
TODO: ここに画像が欲しい
$x_1, x_2$は入力信号、$y$は出力信号、$w_1,w_2$は重み、$\theta$は閾値を表す。
y = 0; (w_1x_1 + w_2x_2 \leqq \theta)\\
y = 1; (w_1x_1 + w_2x_2 \gt \theta)
論理回路との関連
ANDゲート、NANDゲート、ORゲート、XORゲートをパーセプトロンで表現する。
- 線形と非線形
- 多層パーセプトロン
- パーセプトロンはXORを実装できないので多層で実装する
3章 ニューラルネットワーク
入力層・中間層・出力層
活性化関数
入力信号の総和を出力信号に変換する関数のこと
- ステップ関数
- シグモイド関数
- ReLU(Rectified Linear Unit)関数
3-5 出力層の設計
ニューラルネットワークは「分類問題」と「回帰問題」の両方に用いることができる。
いわゆる回帰分析とは、原因となる無数の変数$x$と結果となる無数の変数$y$の間に、モデルを求める分析手法のことと言える。例えば年齢(x)と年間支出(y)を回帰分析してモデルを求める、など。
回帰問題には恒等関数(入ってきたものをそのまま出力)
分類問題にはソフトマックス関数 を使う
ソフトマックス関数
ソフトマックス関数の出力は0から1.0の間の実数になる。
ソフトマックス関数の出力の総和は1になる。
以上の性質から、ソフトマックス関数の出力を「確率」として解釈することができる。
3-6 MNISTデータセット
ソースはgithubにサンプルコードあり。
4章 ニューラルネットワークの学習
訓練データから最適な重みパラメータの値を自動で獲得することを指す。
ニューラルネットワークが学習を行えるようにるために「損失関数」という指標の導入
4-1 データから学習する
4-1-1 データ駆動
人の経験や直感を手掛かりに試行錯誤を重ねるようなアプローチを排する。
MNISTの手書きの数字の「5」を認識するプログラムを実装することをゴールと考える。
「5」を認識するアルゴリズムを捻り出す代わりにデータを活用して解決する。
データから画像の特徴量を抽出する。
機械学習の問題に対して2つのアプローチ(人が介在する/しない)
- 手書き数字画像→人の考えたアルゴリズム→答え
- 手書き数字画像→人の考えた特徴量→機械学習(SVM, KNN)→答え
- 手書き数字画像→ニューラルネットワーク→答え
4-1-2 訓練データとテストデータ
訓練データ(教師データ)だけを使って学習を行い、テストデータを使ってモデルを評価する。
テストデータを訓練データに混ぜるとそのデータセットだけに適応してしまう(過学習 overfitting)ことが起こり得る。誰が書いた手書き数字にも対応できる汎用的な能力がモデルには必要。
4-2 損失関数
ニューラルネットワークの学習の良し悪しの状態を表す一つの指標を「損失関数(loss function)」という。任意の関数を用いることができるが一般的には
- 2乗和誤差
- 交差エントロピー誤差
を用いる。
損失関数は「悪さ」を表す。ニューラルネットワークが教師データに対してどれだけ適合していないか、一致していないかを表す。損失関数にマイナスを掛けると逆にどれだけ性能が良いかを表す指標として解釈することができる。
4-2-1 2乗和誤差
E = \frac{1}{2}\sum_{k}(y_k-t_k)^{2}
tを正解ラベルとする。yは訓練データをニューラルネットワークからのアウトプット。
正解は数字の2である。
1番目のyは2の可能性が最も高い学習結果になっているため、損失関数の数値も小さいが、2番目のyは7の可能性が最も高い学習結果になっているため、一つ目の損失関数よりも数値が高い
>>> import numpy as np
>>> def mean_squared_error(y, t):
... return 0.5 * np.sum((y-t)**2)
...
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> len(t)
10
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> len(y)
10
>>> mean_squared_error(np.array(y), np.array(t))
0.097500000000000031
>>> y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> len(y)
10
>>> mean_squared_error(np.array(y), np.array(t))
0.59750000000000003
4-2-2 交差エントロピー誤差
E = -\sum_{k}t_klogy_k
実質的には正解ラベルが1に対応する出力の対数を計算するだけ。
「2」が正解ラベルでそれに対応するニューラルネットワークの出力が0.6の場合、交差エントロピー誤差は-log0.6=0.51となる。また、ニューラルネットワークの出力が0.1の場合は-log0.1=2.30となる。やはりこれも損失関数の値が小さい方が教師データにより適合していることを示している。
>>> def cross_entropy_error(y, t):
... delta = 1e-7
... return -np.sum(t * np.log(y+delta))
...
>>> t
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
>>> y
[0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
>>> y1 = y
>>> y0 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> len(y0)
10
>>> cross_entropy_error(np.array(y0), np.array(t))
0.51082545709933802
>>> cross_entropy_error(np.array(y1), np.array(t))
2.3025840929945458
4-2-3 ミニバッチ学習
訓練データ全ての損失関数の和を求めたい場合(交差エントロピー誤差)、式は次のようになる。
E = - \frac{1}{N}\sum_{n}\sum_{k}t_{nk}logy_{nk}
データがN個あり、最後にNで割って正規化している。平均の損失関数を求めている。
MNISTのデータは6万だが、ビッグデータともなると個別に損失関数を計算するのは現実的ではない。そこでテレビの視聴率の計測のように6万の中から無作為に100個を抽出し学習を行うような学習手法をミニバッチ学習という。
4-2-4 [バッチ対応版]交差エントロピー誤差の実装
TODO: もうちょっと下記の式中のNumpyの処理を理解する必要あり
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
# 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
if t.size == y.size:
t = t.argmax(axis=1)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arrange(batch_size), t])) / batch_size
4-2-5 なぜ損失関数を設定するのか?
認識精度を指標にできないので損失関数を設定する。認識精度を指標にすると、パラメータの微分がほとんどの場所で0になってしまうから。
認識精度は活性化関数の「ステップ関数」に見られるように、パラメータの微小な変化にはほとんど反応を示さず、ある時いきなり不連続に変化する。これに対比し、sigmoid関数は曲線の傾き(関数の微分の結果)は連続的に変化する。
4-3 数値微分
勾配法を理解するために微分が前提知識として必要
4-3-1 微分
1e-50という数値を使うと「丸め誤差(rounding error)」問題が発生するので、1e-4を使うと良い結果が得られることが既知のこととなっている。
\frac{df(x)}{d_x} = \lim_{h \to 0}\frac{f(x + h) - f(x)}{h}
通常の導関数の公式は上記だが、実装にあたっては丸め誤差問題から下記のような実装になる。
>>> def numerical_diff(f, x):
... h = 1e-4
... return (f(x+h) - f(x-h)) / (2*h)
...
4-3-2 数値微分の例
4-3-3 偏微分
複数の変数からなる関数の微分を偏微分という。
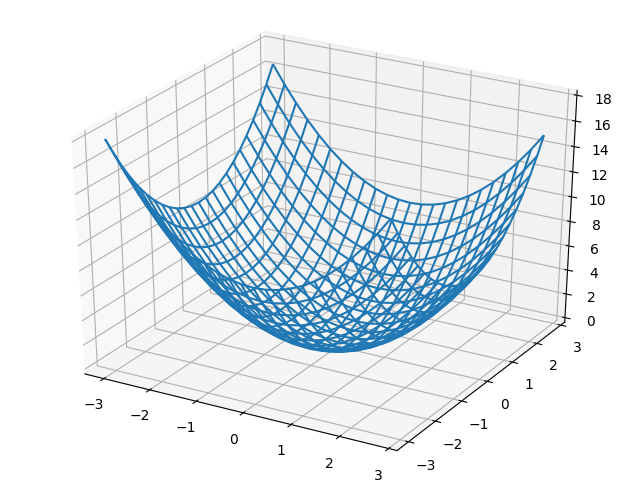
f(x_0, x_1) = x_0^2 + x_1^2
$x_0$と$x_1$のどちらの変数に対しての微分であるのかを区別する必要がある。
$\frac{\partial f}{\partial x_0}$, $\frac{\partial f}{\partial x_1}$というように書く
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x0, x1):
return x0 ** 2 + x1 ** 2
x0 = np.arange(-3, 3, 0.25)
x1 = np.arange(-3, 3, 0.25)
X0, X1 = np.meshgrid(x0, x1)
Y = func(X0, X1)
fig = plt.figure()
ax = Axes3D(fig)
ax.plot_wireframe(X0, X1, Y)
plt.show()
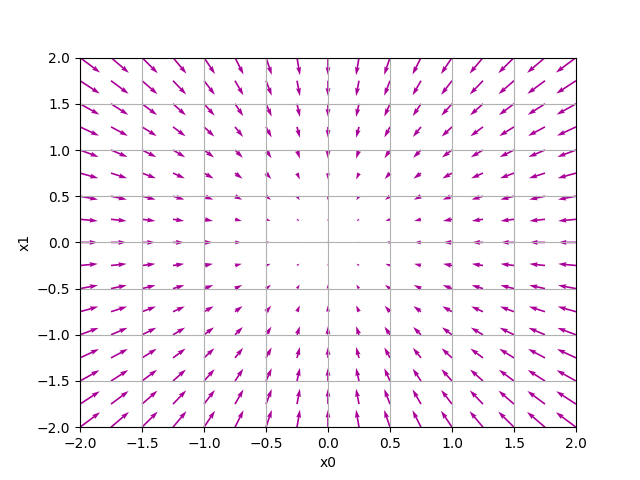
4-4 勾配
全ての変数の偏微分をベクトルとしてまとめたものを勾配(gradient)という。
\begin{pmatrix}
\frac{\partial f}{\partial x_0}, \frac{\partial f}{\partial x_1}
\end{pmatrix}
勾配は関数$f(x_0, x_1)$の「一番低い場所(最小値)」を指す。「一番低い場所」から遠く離れれば離れるほど、矢印の大きさも大きくなる。だが、実際には必ずしもそうなるとは限らない。より正確に言うと、勾配が示す方向は、各場所において関数の値を最も減らす方向になっている。
4-4-1 勾配法
損失関数は複雑。パラメータ空間は広大でどこに最小値を取る場所があるのか見当がつかない。そこで勾配をうまく利用して関数の最小値を探す。
関数の極小値、最小値、鞍点(saddle point)と呼ばれる場所では勾配が0になるが、関数の中でそこが最小値とは限らないことに注意。
勾配法は現在位置から一定の距離だけ移動し勾配を求め、さらに一定距離を詰めていくということを繰り返す方法。
最小値を探す場合、勾配降下法(gradient descent method)と呼び、最大値を探す場合は勾配上昇法(gradient ascent method)と呼ぶ。
勾配法を数式で示すと下記の通り。数式中の$\eta$はエータと呼ぶらしい。
x_0 = x_0 - \eta\frac{\partial f}{\partial x_0} \\
x_1 = x_1 - \eta\frac{\partial f}{\partial x_1}
$\eta$は更新の量を表し学習率(learning rate)とも呼ばれる。
4-4-2 ニューラルネットワークに対する勾配
ニューラルネットワークの学習における勾配とは、重みパラメータに関する損失関数の勾配。損失関数とはニューラルネットワークの学習の良し悪しの状態を表す一つの指標。
形状が2x3の重みWを持つネットワークがあり、損失関数をLで表すとすると、勾配は$\frac{\partial L}{\partial W}$と表すことができる。実際に式で表すと下記。
{
W =
\begin{pmatrix}
w_{11} \quad w_{21} \quad w_{31} \\
w_{12} \quad w_{22} \quad w_{32}
\end{pmatrix}
} \\
{
\frac{\partial L}{\partial W} =
\begin{pmatrix}
\frac{\partial L}{\partial W_{11}} \quad \frac{\partial L}{\partial W_{21}} \quad \frac{\partial L}{\partial W_{31}} \\
\frac{\partial L}{\partial W_{12}} \quad \frac{\partial L}{\partial W_{22}} \quad \frac{\partial L}{\partial W_{32}}
\end{pmatrix}
}
$\frac{\partial L}{\partial W}$の各要素はそれぞれの偏微分から構成される
4-5 学習アルゴリズムの実装
- 前提
- 重みとバイアスを訓練データに適応するように調整することを「学習」という
- STEP1 ミニバッチ
- STEP2 勾配の産出
- STEP3 パラメータの更新
- STEP4 繰り返す
4-5-1 2層ニューラルネットワークのクラス
勾配法を使っての計算にすごく時間がかかるが、誤差逆伝播法を使うととても早く計算が完了する。
4-5-2 ミニバッチ学習の実装
4-5-1を用いてミニバッチ処理をする
4-5-3 テストデータで評価
過学習を起こさないように損失関数の値を減らしていく。
1エポック(epoch)毎に訓練データとテストデータの認識精度を記録するとよい。
epochとは学習において訓練データを全て使い切ったときの回数に対応する。例えば10,000個の訓練データに対して100個のミニバッチで学習する場合、勾配法を100回繰り返したら全ての訓練データを使い切って1epochとなる。