Jupyter Notebookと"R" カーネル (IRkernel)を使って「全体の一部が見えているモデル」を試してみた.ねた本は,岩波データサイエンス Vol.1 である.
全体の一部が観測できるモデル ~ 観測値が二項分布
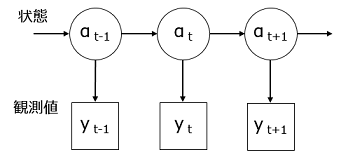
まず状態空間モデルの概念図を示す.
真の値,状態値はシーケンシャルに変化するものとし,実際に観測する値は,状態値の値にある「ばらつき」が加算される,というモデルが一般的な状態空間モデルである.今回扱うのは,状態に対して「ばらつき」のようなノイズを与えるのではなく,「観測では状態の一部分しか見えない」というモデルを考える.
N_{ti}^{obs} \sim Binomial(N_t, p)
1回の観測において5回ずつカウントデータを採取し,その観測をシーケンシャルに50回行う.$ N_{ti}^{obs} $ はt回目の観測におけるi回目のカウントデータで,それは真の値, $ N_t $ の二項分布に従うというモデルである.
また,真の値は今回,ポアソン分布に従うとし,ポアソン分布のパラメータとして期待値 $ \lambda_t $ を与える.このときのシステムモデルは以下となる.
N_{t} \sim Poisson( \lambda_t ) \\
log\ \lambda_t \sim Normal( log\ \lambda_{t-1}, \sigma^2) \\
少し込み入っているが,下の分析データを生成するコードを見た方が,状況が明確になるかと思う.(作成したJupyter Notebookのスナップショットです.Jupyter Notebook + IRkernel とても便利です.)
状態空間モデルのBUGSコードは,以下のようになる.
(前略)
## Observation model
for (t in 1:nt) {
lambda[t] <- exp(log.lambda[t]);
N[t] ~ dpois(lambda[t]);
for (i in 1:nr) {
Nobs[t, i] ~ dbinom(p, N[t]); # 観測値は状態値から決まる二項分布
}
}
## System model
for (t in 2:nt) {
log.lambda[t] ~ dnorm(log.lambda[t - 1], tau); # 状態値は一つ前の状態値から決まる正規分布
}
(後略)
発見確率 p=0.6 条件の計算結果
上記のBUGSコードを{rjags}パッケージを用いて計算を行った結果をプロットする.
Fig.1 Observed point & Simulated distribution (p=0.6)
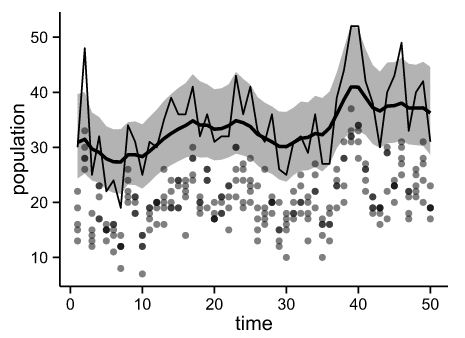
各ドットは,観測値を示す.
(一部,濃いドットがありますが,2つ以上の点が重なったものです.)
細い線が,(事前に生成した)真の値.太い線がJAGSのシミュレーションで求めた平均値,灰色部が95%信用区間を示す.きちんと参考文献と同じプロットが再現できている. 設定した条件,
発見確率 = 観測数 / 真の個数 = 0.6 (60%)
も上図にうまく反映されているように見える.
(ドット群が線位置の約60%を中心に散らばっているように見えるかと思います.)
発見確率を半分,p=0.3 としてみる
ここからが今回,調べたかった内容になる.全体の状態の30%しか見ない条件だとどのようになるか?データ生成のコードを以下のようにした.
set.seed(31415)
nt <- 50 # observing time
nr <- 5 # counting times per 1-observation
p <- 0.3 # observation ratio (changed)
log.lambda <- numeric(nt)
log.lambda[1] <- log(30) # initial value
for (t in 2:nt) {
log.lambda[t] <- log.lambda[t - 1] + rnorm(1, 0, 0.1)
}
## true numbers
N <- rpois(nt, exp(log.lambda))
## observed numbers
Nobs <- sapply(1:nt, function(t) rbinom(nr, N[t], p))
Random Seed を前回と同じ値に固定,pの値のみを0.3に変更している.シミュレーション結果は下図になった.
Fig.2 Observed point & Simulated distribution (p=0.3)
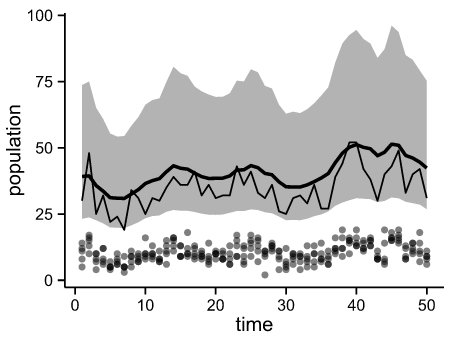
各ドットは観測値,細い線は(事前に用意した)真の値,太い線がシミュレーションで求めた平均値である.細い線は前回(Fig.1)と同じ線であることが確認できる.Fig.1 と異なる特徴は,灰色部の95%信用区間が広がったことである.母集団からのサンプルの割合が減ったため,「95%信用区間が広がった」,「大きなばらつきを想定しなければならなくなった」となったと考えられる.
一つ奇妙に思ったのが,シミュレーションの平均値(太線)が真の値(細線)から上にオフセットしているように見える点である.これについては,観測値に対しあてはめた統計分布,二項分布(Binomial Distribution)の特徴を思い出す必要がある.
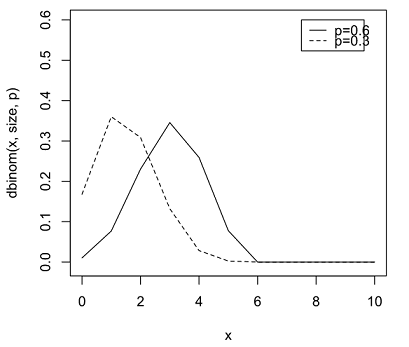
p=0.6 では,分布は skew が微小の状態,左右対称であるのに対し,p=0.3 は,分布が skew が大きくなっているのが分かる.このような非対称な分布を当てはめた結果, Fig.2 のようなオフセット(太線~細線)が発生したと考えられる.
状態空間モデルとして,「全体の一部しか見えない」モデルを取り扱えることが分かったが,あまりデータが少ないとやはり推定が「ぼやける」ことになってしまう.「データは重要」ということで納得した次第である.
参考文献 (web site)
「岩波データサイエンス」サポートページ
https://sites.google.com/site/iwanamidatascience/統計学入門,東京大学教養学部統計学教室編
http://www.utp.or.jp/bd/978-4-13-042065-5.html状態空間モデルを試す(Jupyter Notebook + IRkernel) - Qiita
http://qiita.com/TomokIshii/items/0cec5c8c0da8fd3d0b15