1教師なし学習
1.1 主成分分析(PCA)
Principal Components Analytics
「できるだけ情報を多く残したまま、主成分(データ構造)を求める」
高次元のデータの場合、直感的にデータ構造が分からない。このときに、低次元に落として、どういう分布のデータなのか分かりやすくする手法が主成分分析である。
次元を落とすというのは、多数の変数がある場合に、相関がある似たような変数は減らすことが出来るはずであるという考えのもとに、変数(特徴)を減らす。また、問題に対して全然関係ない変数を減らすことも出来るはずである。
ここで、次元を落とす次元削減をするときに、守るべき点が2つある。
- 分散最大化
- 誤差最大化
1.1.1. 次元削減の際のルール
分散最大化
主成分分析で次元削減をする際には、まず、データの広がりが最も大きくなる方向を見つけ、それを第1主成分とする。これが分散最大化である。
データに広がりがあるという事は、情報量が多いということである。これはつまり、似たようなデータには、情報として価値がないが、違いの大きいデータにはそれだけ価値があるので、分散の大きさは重要であるということである。
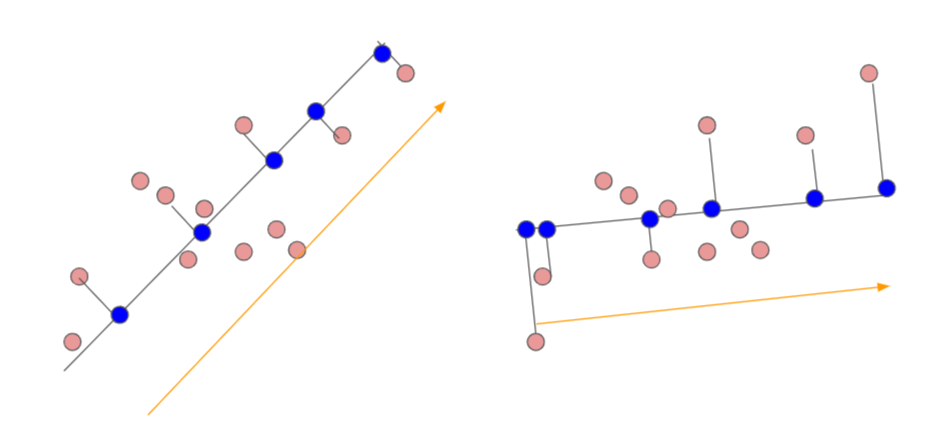
下の図のように第1主成分空間へ、各データを直行射影した結果、左の図のほうが、右よりも、第1主成分空間上の分散が大きい。
誤差最大化
直行射影をする際に、垂直の線の長さが最も小さくなるように主成分を設定することを意味する。
1.1.2. 分散最大化の定式
2次元データを1次元の直線上へ射影(次元削減)することを考える。
n個の2次元データ集合${x_n}$を、1次元の直線$y=w_1 x_1 + w_2 x_2 $へ射影するとすると、
y_i = w_1 x_1 + w_2 x_2 = w^T x_i
上記のyの分散を最大にするwを求めればよい。wはここでは、第1主成分の傾きを表している。もっとも都合の良い傾きを求めるという事になる。
1.1.3. 分散最大化の直線の求め方
分散を求めるには、まず平均
第1主成分の平均: \; \bar{y} = \frac{1}{n} \sum_{i=1}^n y_i = \frac{1}{n} \sum_{i=1} (w_1 x_1 + w_2 x_2) = w_1 \bar{x_1} + w_2 \bar{x_2} = w^T \bar{x}
第1主成分の分散: \; s_y^2 = \frac{1}{n} \sum_{i=1} ( y_i - \bar{y})^2
求めたいのはこの分散を最大化するWであるので、展開していく。
第1主成分の分散: \; s_y^2 = \frac{1}{n} \sum_{i=1} ( y_i - \bar{y})^2 \\
= \frac{1}{n} \sum_{i=1}^n \left( w_1 (x_{i1} - \bar{x_1} ) + w_2 (x_{i2} - \bar{x_2} ) \right)^2 \\
= w_1^2 s_{11} + 2 w_1 w_2 s_{12} + w_2^2 s_{22} \\
= w^T S w
Sは分共分散行列
S =
\begin{pmatrix}
s_{11} & s_{12} \\
s_{21} & s_{22}
\end{pmatrix}
情報損失の表現
次元削減をすると、当然であるが、情報の損失が発生する。
例えば、2次元データを1次元に射影する場合だと、主成分の直線の上にあるデータと下にあるデータが、射影された結果、同じ直線上の同じ点にしか見えないという結果が発生する可能性がある。
そこで、主成分分析では、この情報量がどれだけ残っているかを示す表現方法がある。
その表現には、固有値 $\lambda$を使う。
第1から第k主成分までの情報量が、全体(第p主成分)のどれだけの割合かを見る場合、
累積寄与率: \;
\frac{\lambda_1 + \lambda_2 + , \cdots, \lambda_k}
{\lambda_1 + \lambda_2 + ,\cdots, \lambda_k, \cdots, \lambda_p}
この値は高く保っておく必要がある。
参考
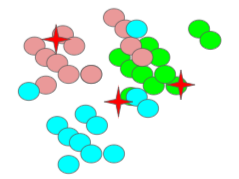
1.2 k-means
クラスタリングの手法である。
最初に適当なk個のクラスタに分けておき、その後、近いデータをクラスタに分類しなおすことを繰り返す。
1.2.1. k-meansの手順
- クラスタ分類の初期値(各クラスタのデータ中心)を決める
- 各データを最も近いクラスタ中心のクラスタに分類する
- 各クラスタのデータ重心を求める。
- 上記の2、3を、データ重心が動かなくなるまで繰り返す。
1.2.2. エルボー法
k-meansは、最初に、クラスタ数を最適値を考えるのが大変。
これを自動で出してくれるのがエルボー法である。
なお、データ重心が動かなくなってからは、何度計算しても結果はたいして変わらない。
エルボー図の肘が曲がった後は、たいしてかわらないので、繰り返し回数としてはこのあたりが適切。
2 教師あり学習
2.1 k近傍法(k-NN)
クラスタリングの手法である。
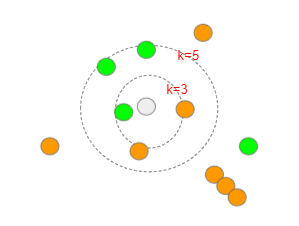
既にクラス分けされている集団の中に新しいデータを入れたとき、その近傍にあるk個のデータを見て、多数決でクラス分けする。
k=1の場合は、最近傍法といわれる。
k-NNは、怠惰学習というレッテルを張られている。これは、教師データから、最適な分類器を学習によって獲得しないことに由来する。
教師データが入力されれば、それを単に覚えておくだけでよいからである。