ランダムウォークをJuliaでシミュレーションする

動機

以前、1次元量子ウォークについての実装のための簡単な解説記事を書きましたが、ランダムウォークの実装の仕方（または自分の書き方）についても忘れないためにメモとして書いておく。
「１次元量子ウォークをJuliaでシミュレーションする」
https://qiita.com/QQQ_0018/items/36bffd48975622f7fb43

目的

ランダムウォークの理論式から得られる任意ステップの確率分布を、実際に乱数を発生させて実験的なランダムウォークと比較する。このとき、同一ステップで何回試行させると理論結果に近づくのか確認する。

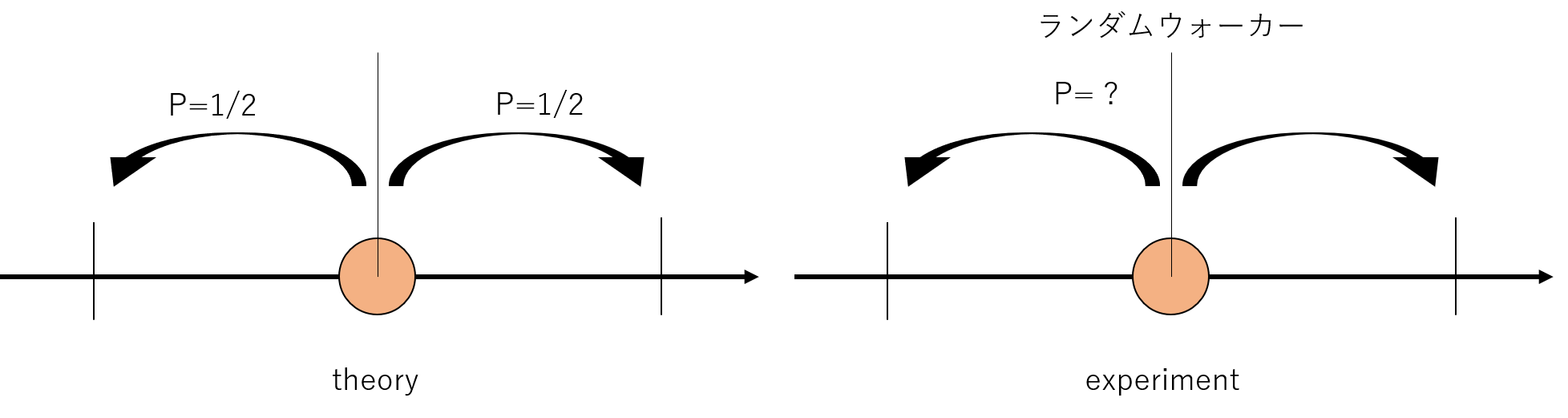
設計

1次元の場合)

ウォーカが決められたステージ(1次元なら直線、2次元なら平面)の端にいるときには、固定端条件を採用.

function x_koteitan(x,n)
    if n >= x >= 1.0 
        return x
    elseif x < 1.0
        return x = 1
    elseif x > n
        return x = n
    end
end

関数random_walk(loop)は現在の場所posから次の場所next_presentを乱数で決定.
一方で、math_random_walk(n, step)は格子数n(ステージの大きさ)の理論確率分布を比較対象として用意する.

function random_walk(pos)
    #変位を収納する
    if rand(UnitRange{Int8}(0:1)) == 0
        next_present = pos + 1
    else
        next_present = pos - 1
    end
    return x_koteitan(next_present,n)
end

function math_random_walk(n,step)
    prob=zeros(Float64,n)
    prob[div(n,2)] = 1.0
    for t in 0:step
        next_prob = zeros(Float64,n)
        if t == 0
            prob[div(n,2)] = 1
        else
            for x in 2:n-1
                next_prob[x] = 0.5*prob[x-1]+0.5*prob[x+1]
            end
            prob = copy(next_prob)
        end
    end
    return prob
end

ランダムウォークは毎回ステップに対して、存在する座標が変わるので、ある程度誤差を減らすためにに、step数に対して、試行回数loopを行う.　

using ProgressMeter
using Plots
gr()
n = 50
step= 100
loop= 10000
function experiment(loop,step)
    p = Progress(loop)
    xpos=zeros(Float64,n)
    #anim =@animate for i in 1:loop
    for i in 1:loop
        pos = div(n,2)
        for t in 1:step
            pos = random_walk(pos)
        end
        xpos[pos] += 1/loop
        #plot(xpos,marker="o",lw=false,ylim=(0,0.1),size=(300,300),label="experiment")
        #plot!(math_random_walk(n,step),label="theory")
        next!(p)
    end
    #return gif(anim,fps=10)
    return xpos
end
plot(experiment(loop,step),size=(300,300),lw=false,marker=:o,markersize=1.5)
plot!(math_random_walk(n,step))

実装

左がloop=100回、右がloop=10000回試行した結果です. 縦軸は存在確率$P$.

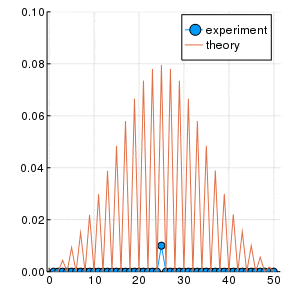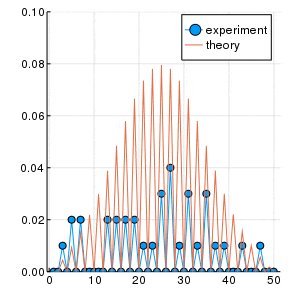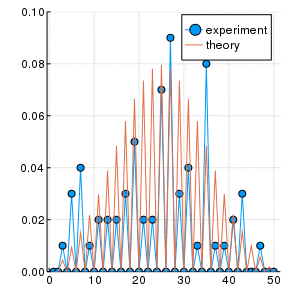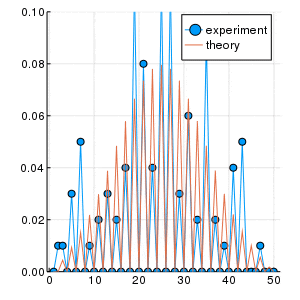
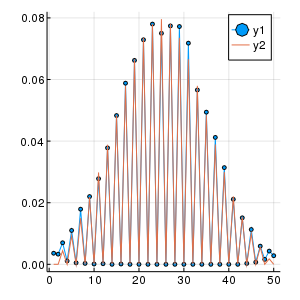
2次元平面ランダムウォークの場合

2次元平面の場合も1次元同様に行う.
2次元平面の理論確率分布の出力関数.

function random_walk(loop)
    one_side = 20
    prob = zeros(Float64,one_side,one_side)
    prob[div(one_side,2),div(one_side,2)]=1.0
    
    progress = Progress(loop)
    #anim=@animate for t in 0:loop
    for t in 0:loop
        if t == 0
            continue
        else
            next_prob = zeros(Float64,one_side,one_side)
            for x in 2:one_side-1, y in 2:one_side-1            
                next_prob[x,y] = copy( 0.25*prob[x0,y] + 0.25*prob[x1,y] + 0.25*prob[x,y0] + 0.25*prob[x,y1] )
            end
        end
        prob = copy(next_prob)
        next!(progress)

    #realtime
    #heatmap(prob,aspect_ratio=1,cbar=true,cbar_lims=(0,0.025))    
    end
    fig = heatmap(prob,aspect_ratio=1,cbar=true,size=(300,300))#,cbar_lims=(0,0.025))#,dpi=300) 
    #gif(anim,fps=20)
    
    return fig

end

function x_koteitan(x,n)
    if n >= x >= 1.0 
        return x
    elseif x < 1.0
        return x = 1
    elseif x > n
        return x = n
    end
end

function y_koteitan(y,n)
    if n >= y >= 1.0 
        return y
    elseif y < 1.0
        return y = 1
    elseif y > n
        return y = n
    end
end

function random_walk_2(array)
    present = zeros(Int64,1,2)
    present[1,:] = copy(array)
    #x,y方向の変位を収納する箱
    delta   = zeros(Int64,1,2)
    #x,y方向をランダムに指定するため
    delta_index = rand(UnitRange{Int8}(1:2))#1ならｘ、２ならy
    #変位を収納する
    if rand(UnitRange{Int8}(0:1)) == 0
        delta[delta_index] = 1
    else
        delta[delta_index] = -1
    end
    
    #t+1秒後の座標
    next_present = present + delta
    x = x_koteitan(next_present[1],n)
    y = y_koteitan(next_present[2],n)
    final_present=[x ,y]
    
    return final_present
end

using ProgressMeter
using Plots
gr()
const n = 20
const step= 9
const loop= 500
function experiment_2(loop,step)
    p = Progress(loop)
    xpos=zeros(Float64,n,n)
    anim=@animate for i in 1:loop
        pos = [div(n,2),div(n,2)]
        for t in 1:step
            pos = random_walk_2(pos)
        end
        xpos[pos[1],pos[2]] += 1.0/loop
        heatmap(xpos,aspect_ratio=1,size=(300,300))
        next!(p)
    end
    return gif(anim,fps=30)
end
experiment_2(loop,step)

300回試行したときの動画です. 左図が理論分布. 右がランダムウォーク.

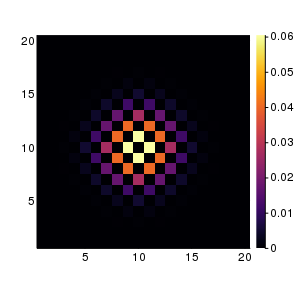
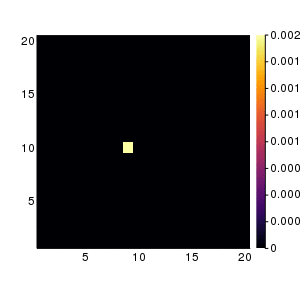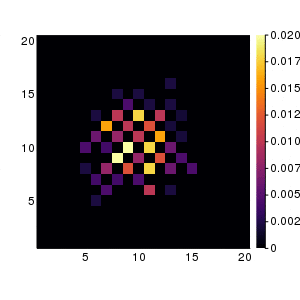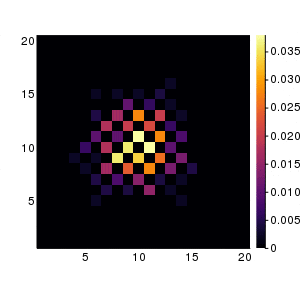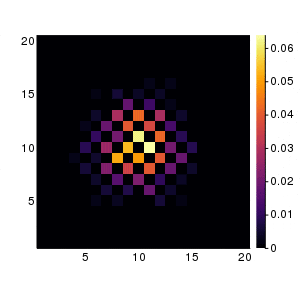
まとめ

ランダムウォークの理論計算と乱数による実験を比較した。1次元だと1万回以上試行しないと理論値と一致しないことが分かった。一方で2次元だと500回程度の施行でおおむね一致する。