以下の統計検定2級対策動画で用いられているスライドの一部です。
このスライドで学ぶこと
ある リゾートホテルの宿泊客数 のデータを例に、時系列データ分析の基本的な手法を学びます。
- ゴール: データから季節ごとのパターンを数値化する 「季節指数」 を算出する
- 手法: 「移動平均法」 というポピュラーな分析手法をステップバイステップで実践する
まずは具体的な計算を通じて、手法の全体像を掴んでいきましょう。
以下の3年分の 四半期別宿泊客数 データから、季節指数を算出してみましょう。
| 年 | 四半期 | 宿泊客数 (原数値) |
|---|---|---|
| 1年目 | 第1四半期 | 120 |
| 第2四半期 | 180 | |
| 第3四半期 | 250 | |
| 第4四半期 | 150 | |
| 2年目 | 第1四半期 | 140 |
| 第2四半期 | 210 | |
| 第3四半期 | 280 | |
| 第4四半期 | 170 | |
| 3年目 | 第1四半期 | 160 |
| 第2四半期 | 240 | |
| 第3四半期 | 310 | |
| 第4四半期 | 190 |
Step 1: データの流れを掴む (移動平均の計算)
まず、短期的なブレをならして、データ全体の 長期的な傾向 を抽出します。
- 移動平均: 連続する一定期間のデータの平均値を計算し、それを順次ずらしていく手法。
- 今回は四半期データ (周期4) なので、 4期移動平均 を使います。
ポイント
偶数期間 (4期) の移動平均を計算すると、平均値の時点が期間の 真ん中 (例: 2.5期目) にずれてしまいます。
これを補正するため、 「中心化移動平均」 という工夫を行います。
Step 1: 中心化移動平均の計算結果
中心化移動平均 (CMA) は、連続する2つの移動平均の平均値です。
- 1回目の4期移動平均: $(120+180+250+150)/4 = 175.0$
- 2回目の4期移動平均: $(180+250+150+140)/4 = 180.0$
- 1年目第3四半期のCMA: $(175.0+180.0)/2 = 177.5$
| 年 | 四半期 | 原数値 (Y) | 中心化移動平均 (CMA) |
|---|---|---|---|
| 1 | 3 | 250 | 177.50 |
| 4 | 150 | 183.75 | |
| 2 | 1 | 140 | 191.25 |
| 2 | 210 | 197.50 | |
| 3 | 280 | 202.50 | |
| 4 | 170 | 208.75 | |
| 3 | 1 | 160 | 216.25 |
| 2 | 240 | 222.50 |
Step 2: 季節性の抽出 (比率の計算)
次に、元のデータが長期的な傾向 (CMA) から どれだけ乖離しているか を比率で求めます。
- この比率には、 「季節変動」 と 「不規則変動」 の2つが含まれています。
$$
比率 = \frac{原数値 (Y)}{中心化移動平均値 (CMA)}
$$
| 年 | 四半期 | 原数値 (Y) | CMA | 比率 (Y / CMA) |
|---|---|---|---|---|
| 1 | 3 | 250 | 177.50 | 1.409 |
| 4 | 150 | 183.75 | 0.816 | |
| 2 | 1 | 140 | 191.25 | 0.732 |
| 2 | 210 | 197.50 | 1.063 | |
| ... | ... | ... | ... |
Step 3: 季節ごとの特徴を平均化 (未補正季節指数)
同じ季節 (例: 第1四半期) ごとにStep 2で求めた比率を平均します。
-
この操作により、突発的な 不規則変動が相殺 され、その季節に固有のパターンが浮かび上がります。
-
第1四半期: $(0.7320 + 0.7399) / 2 = 0.7360$
-
第2四半期: $(1.0633 + 1.0787) / 2 = 1.0710$
-
第3四半期: $(1.4085 + 1.3827) / 2 = 1.3956$
-
第4四半期: $(0.8163 + 0.8144) / 2 = 0.8154$
これらを 「未補正の季節指数」 と呼びます。
Step 4: 季節指数の補正 (なぜ補正が必要か?)
理論上、1年を通した季節指数の 合計は周期の長さ (今回は4) になるべきです。
しかし、計算してみると...
$$
0.7360 + 1.0710 + 1.3956 + 0.8154 = 4.0180 \neq 4
$$
ズレが生じているため、合計が ちょうど4になるように 全体を調整 (補正) する必要があります。
-
補正係数の計算
$$
補正係数 = \frac{周期}{未補正季節指数の合計} = \frac{4}{4.0180} \approx 0.99552
$$
Step 4: 補正後季節指数の算出と解釈
各未補正季節指数に 補正係数 を掛けて、最終的な季節指数を算出します。
- 第1四半期 (補正後): $0.7360 \times 0.99552 \approx 0.733$
- 第2四半期 (補正後): $1.0710 \times 0.99552 \approx 1.066$
- 第3四半期 (補正後): $1.3956 \times 0.99552 \approx 1.389$
- 第4四半期 (補正後): $0.8154 \times 0.99552 \approx 0.812$
| 四半期 | 補正後季節指数 | 解釈 |
|---|---|---|
| 第1四半期 | 0.733 | 平均より 26.7% 少ない |
| 第2四半期 | 1.066 | 平均より 6.6% 多い |
| 第3四半期 | 1.389 | 平均より 38.9% 多い (繁忙期) |
| 第4四半期 | 0.812 | 平均より 18.8% 少ない |
Step 5: 季節変動の影響を取り除く (季節調整)
算出した季節指数を使って、元のデータから季節の影響を取り除きます。
この処理後のデータを 「季節調整済み系列」 と呼びます。
- これにより、データ本来の 長期的な傾向 がより明確になります。
$$
季節調整済み系列 = \frac{原数値}{補正後季節指数}
$$
| 年 | 四半期 | 原数値 | 補正後季節指数 | 季節調整済み系列 |
|---|---|---|---|---|
| 1 | 1 | 120 | 0.733 | 163.7 |
| 1 | 2 | 180 | 1.066 | 168.9 |
| ... | ... | ... | ... | ... |
| 3 | 4 | 190 | 0.812 | 234.0 |
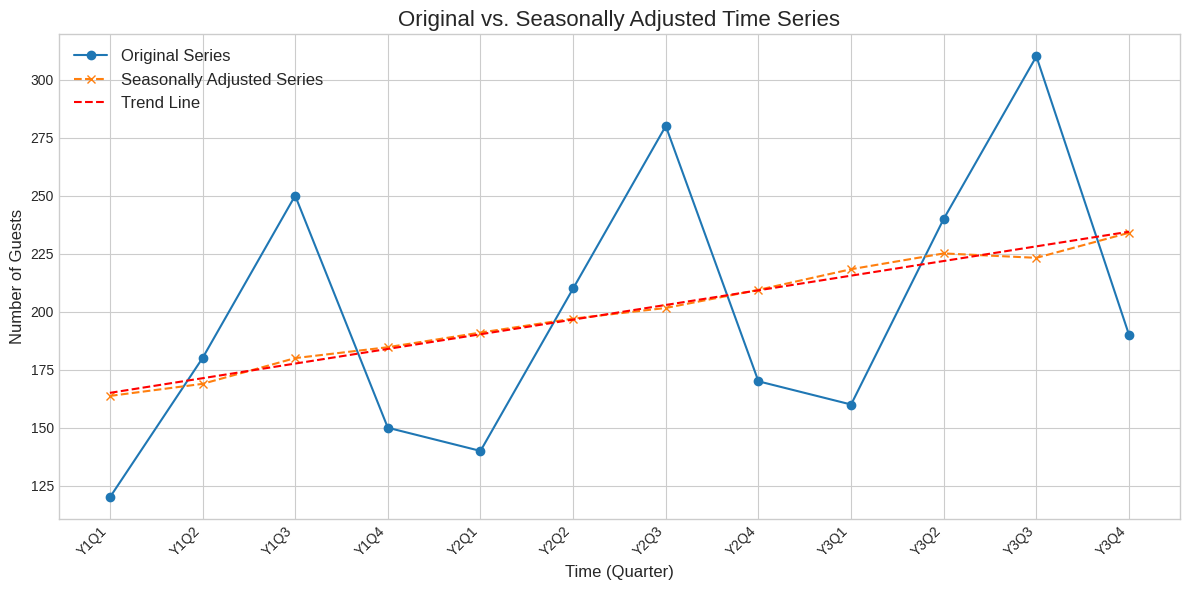
可視化による比較
元のデータ (原数値) と季節調整済み系列をグラフで比較してみましょう。
- 原数値: 季節ごとの凸凹がはっきり見える
- 季節調整済み系列: 凸凹がならされ、 一貫した右肩上がりの傾向 が見やすくなっている
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
# Data preparation (Corrected values)
data = {
'Year': [1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3], 'Quarter': [1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3, 4],
'Original': [120, 180, 250, 150, 140, 210, 280, 170, 160, 240, 310, 190],
'Seasonally_Adjusted': [163.7, 168.9, 180.0, 184.7, 191.0, 197.0, 201.6, 209.4, 218.3, 225.1, 223.2, 234.0]
}
df = pd.DataFrame(data)
df['Time_Index'] = range(1, len(df) + 1)
# Plotting
plt.style.use('seaborn-v0_8-whitegrid')
fig, ax = plt.subplots(figsize=(12, 6))
ax.plot(df['Time_Index'], df['Original'], marker='o', linestyle='-', label='Original Series')
ax.plot(df['Time_Index'], df['Seasonally_Adjusted'], marker='x', linestyle='--', label='Seasonally Adjusted Series')
# Add trend line for seasonally adjusted series
z = np.polyfit(df['Time_Index'], df['Seasonally_Adjusted'], 1)
p = np.poly1d(z)
ax.plot(df['Time_Index'], p(df['Time_Index']), "r--", label="Trend Line")
ax.set_title('Original vs. Seasonally Adjusted Time Series', fontsize=16)
ax.set_xlabel('Time (Quarter)', fontsize=12)
ax.set_ylabel('Number of Guests', fontsize=12)
ax.set_xticks(df['Time_Index'])
ax.set_xticklabels([f'Y{y}Q{q}' for y, q in zip(df['Year'], df['Quarter'])], rotation=45, ha='right')
ax.legend(fontsize=12)
plt.tight_layout()
plt.show()
ここまでのまとめ:時系列データとは?
ここまでの計算例で扱ってきたデータは 「時系列データ」 と呼ばれます。
-
時系列データ: 時間の経過とともに観測されたデータを、一定の間隔で記録したもの (例: 毎日の株価、月ごとの売上高)
-
4つの変動要因: 時系列データは、以下の4つの要素が組み合わさってできていると考えられます。
- 傾向変動: 長期的な増減の方向性
- 周期変動: 1年を超える、景気循環などのサイクル
- 季節変動: 1年を周期とする規則的なパターン ( 今回分析した対象 )
- 不規則変動: 予測不能なランダムな動き
用語の整理
今回の分析で使った重要な用語を整理しましょう。
-
季節変動
- 1年を周期として観測される、 規則的な変動パターン 。
- 例: 夏の飲料水の売上増、年末の小売店の売上増
-
季節指数
- この季節変動のパターンを 定量的に把握するための指標 。
- 各季節が年平均と比べてどのくらいの水準にあるかを示す。
- (例) 季節指数が 1.2 なら、平均より 20% 高い傾向にあると解釈できる。
手法のまとめ: 移動平均法
今回実践した 「移動平均法」 による季節指数の算出ステップは以下の通りです。
-
中心化移動平均 の計算
長期的な傾向を抽出する
-
(原数値 / 中心化移動平均) の計算
季節性と不規則性を取り出す
-
季節ごとの平均 の計算
不規則性を相殺し、未補正の季節指数を求める
-
季節指数の補正
合計が周期の長さと一致するように調整する
まとめ
- 時系列データ は、 4つの変動要因 から構成される
- 移動平均法 を使うことで、データから 季節変動 を抽出し、 季節指数 として数値化できる
- 季節調整 を行うことで、データ本来の長期的な傾向をより明確に捉えられる