多層ニューラルネットワークによる手書き数字の認識

１．人工知能による認識とは

近年、人工知能の分野が著しい発達を遂げています。
人工知能による物事の認識や判断には、一般的にニューラルネットワークというアルゴリズムが使用されています。
これは工学的なアプローチから自動で学習を行うというもので、人間の脳の働きを模す試みと言えるでしょう。
今回はその一環として、人間が自然と認識するように、コンピュータに手書き数字を認識させてみます。

２．ニューラルネットワークによる画像認識

ニューラルネットワークは、人間の脳神経を模した学習モデルです。
多数の非線形変換を行うことによって、与えられたデータから大変な複雑な結果を生み出すことができる代物です。
画像認識の分野においては、テンプレートマッチングという相関処理をニューラルネットに当てはめることで、画像認識を実現していると言えます。
（語弊はあるでしょうが、画素と輝度から畳み込みを行うという点では、まさしく相関処理なのです。）

今回認識させる画像はMNISTの手書き数字です。

• train-images-idx3-ubyte.gz: training set images (9912422 bytes)
• train-labels-idx1-ubyte.gz: training set labels (28881 bytes)
• t10k-images-idx3-ubyte.gz: test set images (1648877 bytes)
• t10k-labels-idx1-ubyte.gz: test set labels (4542 bytes)

をダウンロードしましょう。
ダウンロードしたところでそのまま使える画像データではありませんので、
公式サイトの以下のドキュメントを参考にして、画像データに変換しましょう。

---

TRAINING SET LABEL FILE (train-labels-idx1-ubyte):

[offset] [type] [value] [description]
0000 32 bit integer 0x00000801(2049) magic number (MSB first)
0004 32 bit integer 60000 number of items
0008 unsigned byte ?? label
0009 unsigned byte ?? label
........
xxxx unsigned byte ?? label
The labels values are 0 to 9.

TRAINING SET IMAGE FILE (train-images-idx3-ubyte):

[offset] [type] [value] [description]
0000 32 bit integer 0x00000803(2051) magic number
0004 32 bit integer 60000 number of images
0008 32 bit integer 28 number of rows
0012 32 bit integer 28 number of columns
0016 unsigned byte ?? pixel
0017 unsigned byte ?? pixel
........
xxxx unsigned byte ?? pixel
Pixels are organized row-wise. Pixel values are 0 to 255. 0 means background (white), 255 means foreground (black).

---

教師信号はオフセット8以降に、訓練データはオフセット16以降に格納されていることがわかります。
よってバイナリファイルとして開いて、画素値（28*28）ごとにバイト列を抽出すれば、画像ファイルを取得することが出来ます。
適当に二値化を行うと、以下のような手書き数字の画像データを60000データ分得ることが出来ます。



これにテストデータを加えたものを、ニューラルネットの学習で使用していきます。

３．多層ニューラルネットワークのモデル

今回使用するニューラルネットのモデルは、以下の要件で定義されています。

• 入力層１層、隠れ層２層、出力層１層
• 活性化関数はすべてsigmoid
• 学習率は0.1で固定
• 学習回数は30000回で固定
• 訓練データは１０種類（０～９）で、各種ごとに１００枚使用
• その他momentumなどの特殊なアルゴリズムは使用しない

単純極まりないニューラルネットワークですが、隠れ層を２層使用していることがポイントでしょうか。
改善すべき点は多々ありますが、ひとまずはこの要件で実践してみます。

コードの実装を以下に示します。

MultiLayerPerceptron_MNIST.py

# 1. Preprocess
import random
# 1.1. Make NeuralLetwork
# 1.1.1. Define Layers
n_hidden = 2
n_layer = n_hidden + 2

# 1.1.2. Define Units
n_unit_i = 7 * 7 + 1
n_unit_h = 20 # all 
n_unit_o = 10

unit_i = [0 for u in range(n_unit_i)]
unit_h1 = [0 for u in range(n_unit_h)]
unit_h2 = [0 for u in range(n_unit_h)]
unit_o = [0 for u in range(n_unit_o)]

# 1.1.3. Initialize weight
w1 = [[random.uniform(-1, 1) for u_before in range(n_unit_i)] for u_after in range(n_unit_h)]
w2 = [[random.uniform(-1, 1) for u_before in range(n_unit_h)] for u_after in range(n_unit_h)]
w3 = [[random.uniform(-1, 1) for u_before in range(n_unit_h)] for u_after in range(n_unit_o)]

# 1.2. Define dataset

import mydatasets

n_data = 100
ipt = mydatasets.inputdata("digit")
res = ipt.load_data2(size=(7, 7), num=n_data)

train = res[0][0]
for k in train:
    for n in k:
        n.insert(0, 1)

def maketeach(kind):
    buf = []
    for o in range(n_unit_o):
        if o == kind:
            buf.append(1) 
        else:
            buf.append(0)
    return buf

# 1.3 Implement forward propagation
import math

# 1.3.1 Define activation fucntion
def sigmoid(z):
    if z > 10: return 0.99999
    elif z < -10: return 0.00001
    else: return 1 / (1 + math.exp(-1 * z))

# 1.3.2 forward propagation

def forward(train_vec):

    for i in range(n_unit_i):
        unit_i[i] = train_vec[i]
    unit_i[0] = 1

    # 1.3.2.1 forward between input-hidden1
    for h1 in range(n_unit_h):
        buf = 0
        for i in range(n_unit_i):
            buf += unit_i[i] * w1[h1][i]
        unit_h1[h1] = sigmoid(buf)
    unit_h1[0] = 1

    # 1.3.2.2 forward between hidden1-hidden2
    for h2 in range(n_unit_h):
        buf = 0
        for h1 in range(n_unit_h):
            buf += unit_h1[h1] * w2[h2][h1]
        unit_h2[h2] = sigmoid(buf)
    unit_h2[0] = 1

    # 1.3.2.3 forward between hidden2-output
    for o in range(n_unit_o):
        buf = 0
        for h2 in range(n_unit_h):
            buf += unit_h2[h2] * w3[o][h2]
        unit_o[o] = sigmoid(buf)

# 1.3.3 back propagation

alpha = 0.1
def backpropagation(teach_vec):

    # 1.3.3.1 get cost
    buf = 0
    for o in range(n_unit_o):
        buf += (teach_vec[o] - unit_o[o]) ** 2
    cost = buf / 2

    # 1.3.3.2 get grad between hidden2-output
    for o in range(n_unit_o):
        for h2 in range(n_unit_h):
            delta = (unit_o[o] - teach_vec[o]) * unit_o[o] * (1 - unit_o[o]) * unit_h2[h2]
            w3[o][h2] -= alpha * delta

    # 1.3.3.3 get grad
    for o in range(n_unit_o):
        for h2 in range(n_unit_h):
            for h1 in range(n_unit_h):
                delta = ((unit_o[o] - teach_vec[o]) * unit_o[o] * (1 - unit_o[o])
                         * w3[o][h2] * unit_h2[h2] * (1 - unit_h2[h2]) * unit_h1[h1])
                w2[h2][h1] -= alpha * delta

    # 1.3.3.4 get grad
    for o in range(n_unit_o):
        for h2 in range(n_unit_h):
            for h1 in range(n_unit_h):
                for i in range(n_unit_i):
                    delta = ((unit_o[o] - teach_vec[o]) * unit_o[o] * (1 - unit_o[o])
                             * w3[o][h2] * unit_h2[h2] * (1 - unit_h2[h2])
                             * w2[h2][h1] * unit_h1[h1] * (1 -unit_h1[h1]) * unit_i[i])
                    w1[h1][i] -= alpha *delta

    return cost

import matplotlib.pyplot as plt
plt_x = []
plt_y = []

n_epoch = 30
n_train = len(train)
n_kind = 10
n = 0
error_threshold = 0.001

print("Backpropagation training is started now.")

def training(n):
    for e in range(n_epoch):
        for d in range(n_data):
            for k in range(n_kind):
                try:
                    n += 1
                    forward(train[k][d])
                    c = backpropagation(maketeach(k))
                    plt_x.append(n)
                    plt_y.append(c)
                    if n % 100 == 0:
                        print("learn num: {0}".format(n))
                    if c < error_threshold and e > n_epoch // 2:
                        print("cost is least than error threshold. (n: {})".format(n))
                        return 1
                except Exception as e:
                    print("n:{}, d:{}, k{}, Error:{}".format(n, d, k, e.args))
                    pass
    return 0

def forecast(train_data, dim):
    forward(train_data)
    res = unit_o
    n = 0
    for r in res:
        if r == max(res):
            max_score = n
        n += 1
    print("max score : {}".format(max_score))
    print("scores is below : ")
    print(res)

    import numpy as np
    import cv2
    mat = []
    row = []
    cnt = 0
    n = 0
    for t in range(1, len(train_data)):
        row.append(train_data[t])
        cnt += 1
        n += 1
        if cnt == 7:
            #print("if statement is called at n:{}".format(n))
            mat.append(row)
            row = []
            cnt = 0
    cv2.imwrite('forecast_input.png', np.array(mat)*255)

    return max_score

def validation(vaild_sets):
    n_dim = 7
    correct = 0
    incorrect = 0
    n_kind = 10
    for d in range(n_data):
        for k in range(n_kind):
            if forecast(train[k][d], n_dim) == k:
                correct += 1
            else:
                incorrect += 1
    total = correct + incorrect
    print("validation result:: correct answer is {} / {}".format(correct, total))

training(n)
plt.plot(plt_x, plt_y)
plt.xlim(0, 30000)
plt.ylim(0.0, 1.51)
plt.show()

valid = res[1][0]
for k in valid:
    for n in k:
        n.insert(0, 1)

validation(valid)

４．実行結果

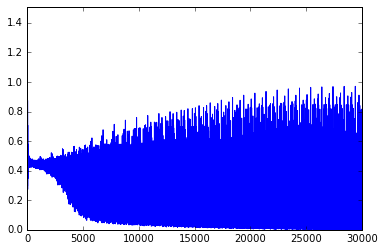
学習回数－誤差のグラフを取ると、以下のような結果が得られました。

ニューラルネットははじめのうち、０（正解）と１（誤り）の区別ができず、中途半端な０．５という判断を下しています。
それが学習とともにどんどん判別できるようになり、正しい結果であれば０、誤った結果であれば１に近い判断を下せるようになっていきます。

これは出力の活性化関数にsigmoidを使用しているために現れる結果です。
sigmoidは０から１までの範囲で値を正規化する効果があり、これによって認識の成否を確率の形で示しています。

また、ヴァリデーションの結果、手書き数字の認識率は84.7%でした。
上記のような原始的なアルゴリズムでこれほどの結果が得られたのであれば、ひとまずは手書き数字の認識に成功したと言えるでしょう。

４．５．実行結果 追記（16/06/06）

実行結果の意味が読み取りづらいとのご指摘を受けたので、解説を付け足します。

まず実行結果のレンジを細かくしてみましょう。

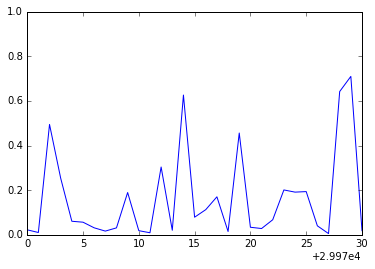
上の図は試行29970...30000までの誤差率のグラフです。
このグラフからは周期性を見て取ることができます。
一の位が0または1のときに誤差が低く、9のときに誤差が高い、といった数字の種別（0...9）毎の周期性です。

この振動は学習のアルゴリズムに起因します。
今回使用したアルゴリズムでは、0の学習が終わったら1の学習を...といった塩梅に、一回ごとに次の種類の数字を学習させています。
そのため試行回数の一の位に応じて誤差率が大幅に変動しているわけです。
連続した試行に直接のつながりはなく、10を法とした試行につながりがあります。
0→10→20→30といった試行で0の認識を学習させ、1→11→21といった試行で1の認識を学習させているわけですね。

各数字によって平均的な認識率は違います。
ある時点のあるモデルは0をよく認識できていて、9はあまり認識できないのでしょう。
だからこそ認識にばらつきができ、振動しているように見えるのです。

そして学習を進めていくうちに、モデルは「理想的な値」というものを学習していきます。
誤差率もまた上昇していきます。
理想値が固まっていくと、ニュートラルな状態に比べて、入力値の乖離度がはっきりしてくるからです。
ここでひとつ、理想値と乖離度の例を見てみましょう。

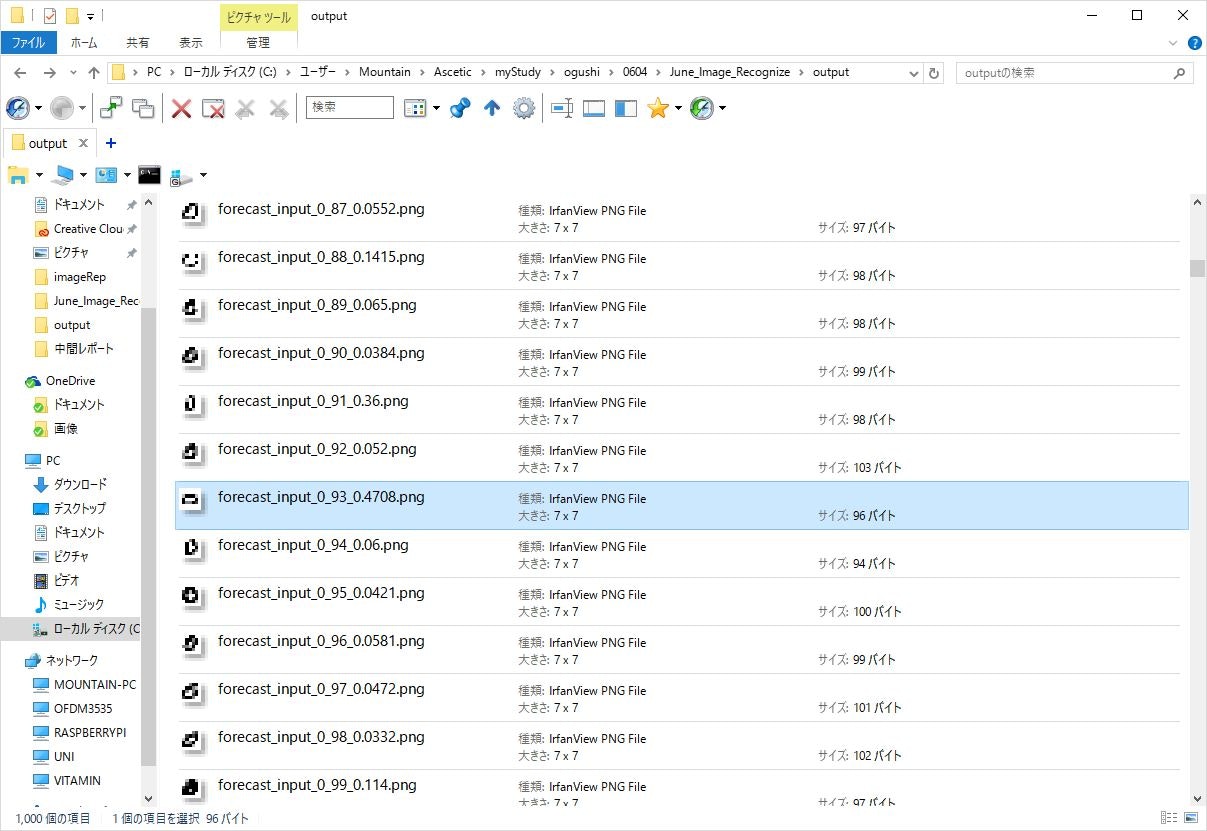
上の図は0のヴァリデーションセットのいち部分を入力した結果と、その誤差率を示しています。
ファイル名のアンダースコアの区切りのうち、最後の部分、拡張子の手前が誤差率です。
誤差率の手前が画像のインデックス番号です。
この画像の中では、93番の入力画像がもっとも高い誤差率（0.4708）を示しています。
このひしゃげた形を見たところ、0であるとは認識しがたい、とモデルが学習したのです。
また上の画像の中では、98番がもっとも誤差率が低いので、右斜に傾いた0こそが、もっとも0の理想形に近いとも学習されているのです。

５．結び

今回はニューラルネットの単純な実装を示しました。
しかし現状のアルゴリズムでは、学習回数と誤差の面でまだまだ不満が残っています。
次回はこの不満点をいくつかのアプローチから解消していきます。