More than 5 years have passed since last update.

主成分分析

Posted at 2017-06-25

例によって、機械学習やその他色々について得た知識を
復習and記事作成の練習and個人の備忘録としてまとめていきます！

今回は、多変量解析の一手法でデータの次元を削減するために用いられる、
"主成分分析"について書いていきます！

⚠︎※※注意※※⚠︎

・出来るだけ専門知識のあまりない人に対して、分かりやすく書くことを目標にしています。
　そのため、厳密に言うと間違っている部分があると思いますがご容赦ください。

・また、ネットで調べたレベルの知識がほとんどなので、
　"厳密に言うと"レベルではなく間違っている箇所があるかもしれません。。
　その場合は非常に申し訳ないです。指摘していただけると幸いです！

主成分分析とは

分析を行うとき、データを可視化して眺めることは非常に大事なことです。
数字ばっかり眺めて見てもあまりよくわからないです。

ですが、多変量データと呼ばれる、多くの変数があるデータを分析するとき、
可視化するのは非常に困難になってしまいます。

困難というか、4変数以上のデータをそのまま可視化することは不可能ですね。笑
かといって２変数や3変数だけ抽出しても、なんか違います。

そういう時に使われるのがこの"主成分分析"です。

主成分分析では、なるべく情報を落とさずに、多次元のデータを低次元に要約します。

そうしていくことで、
「全部の軸を見なくていいから、なにかデータをうまく表現できるような軸でデータを見たい！」
そんな思いに応えてくれます。

なるべく情報を落とさない、とはどういうことでしょうか。

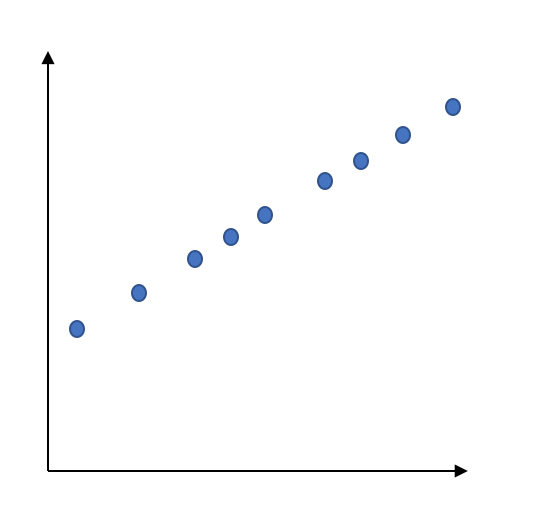
例えば、以下のようなデータがあったとします。

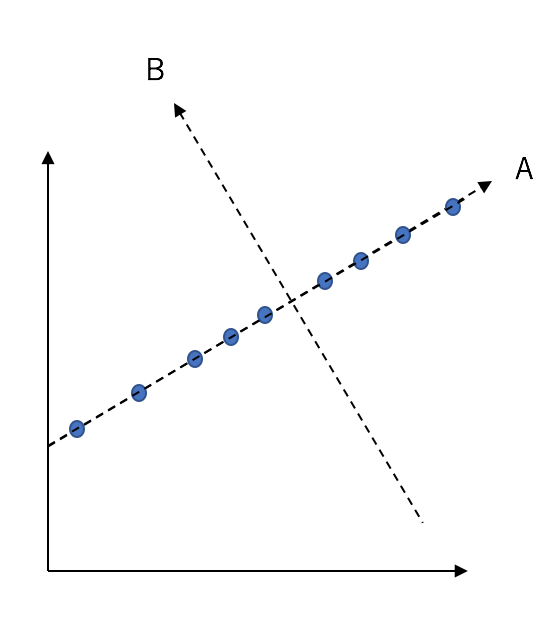
そこで新しく次のA,Bの軸を設定します。

この時、A,Bそれぞれ一軸の視点で見てみると、

というような形になります。

つまりこのデータに対して、
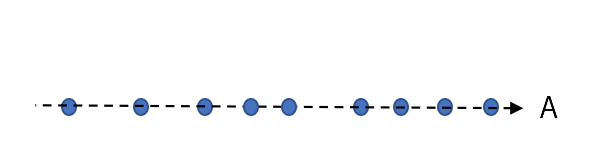
「一番情報を落とさない軸」がAで、
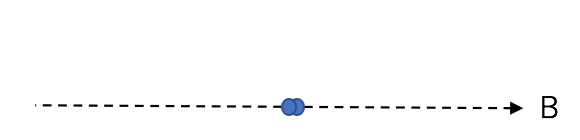
逆に「一番情報を落としてしまう（情報の少ない）軸」がBだと言えます。

これをもう少し具体的な言い方をすると、
「一番情報を落とさない軸」とは、「一番データのばらつきが残る軸」です。

上記を踏まえて、主成分分析の手順を説明します。

Step1. 全てのデータの重心を求めます。

Step2. 重心を通り、データのばらつき(分散)が最大となる方向を見つけます。(第一主成分)

Step3. Step2で見つけた主成分を新しい軸とします。

Step4. Step3の軸に対して直交する方向に対して、ばらつきが最大となる方向を見つけます。(第二主成分)

Step5. Step3~4を、データの次元の数だけ繰り返します。(第三主成分、第四主成分、・・)

N次元のデータに対して、一番情報量の多い第一主成分から順に第N主成分まで出すことができます。

情報量の多い軸＝大事であり、後の軸になればなるほど、情報量は少なくなる＝大事ではなくなる
ので、第一・二(・三)主成分で可視化して、データの関係性をおおまかに判定できます！

可視化することできる具体的な例としては、

たとえば、前回の記事で説明したk-meansにおいては、初めに分割するクラスター数を決めなければなりませんが、
多変量データを見てもいくつのクラスターに分ければいいのか判断できません。

そこでとりあえず主成分分析を行い可視化してデータのおおまかな偏りをみることで、いくつのクラスターに分ければいいかを決める手助けができたりします。

・"主成分分析"は多変量解析の一手法で、次元の削減に用いられる。

・"一番情報量の多い軸"は"一番データのばらつきが大きい軸"である。

・主成分分析は単純な次元削減の他、k-meansにおけるクラスター数の決定などで用いられる。

最後何かサンプルデータで主成分分析を行なってみようと思いましたが、この記事を書いている時のタイミングが悪く、断念しました。。(スミマセン。。)

そしてまだまだ駆け出しのデータサイエンティスト(とはまだ呼べないレベル)として、書けることが少なくなってきました。。

次は何の脈絡もなく、自然言語処理系のことでも書こうかな、と思っています。

ここまで読んでいただき、ありがとうございました！