TensorFlowでチュートリアルデータに頼らず2-3-2のNNを作る

これはなに？

TensorFlowを勉強しようと思って調べてみるとたくさんのチュートリアルがあります。
でも、チュートリアルにないことをやろうとすると一気に詰まります。
（わたしはつまりました。。。。）

ということでチュートリアルに頼らないでニューラルネットワークを作って解いてみたのでメモです。 自分がこういうのあったらよかったな、というメモのみなさんへのおすそ分けです。

さいしょにお詫び

わたしはそんなに機械学習や数学に強いわけではありません！
なので世の中のサンプルを切ったはったして今回のコードを作り上げています。
指摘あったらガンガンとコメントください m__m

いろいろと難しい数式とかの説明は省いていますが、私が説明できるだけの力量を持ち合わせていないからです。。。

あと、ニューラルネットワークとは？ みたいな説明も省いてます。 たくさん良書がすでにあるからです。

では説明スタート！

最初にざっくり全体概要

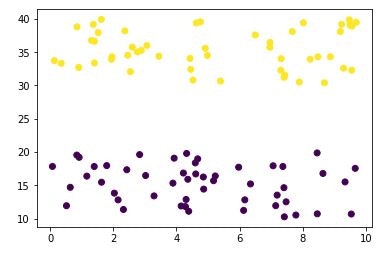
データはこんな感じのものを用意します。

わかりやすいように２つのグループに分けられるデータ群を作って学習データとして使います。 学習させた後に、新たな X と Y を与えて、それが、黄色いグループになるか紫のグループになるか、を分類するニューラルネットワークを作成します。

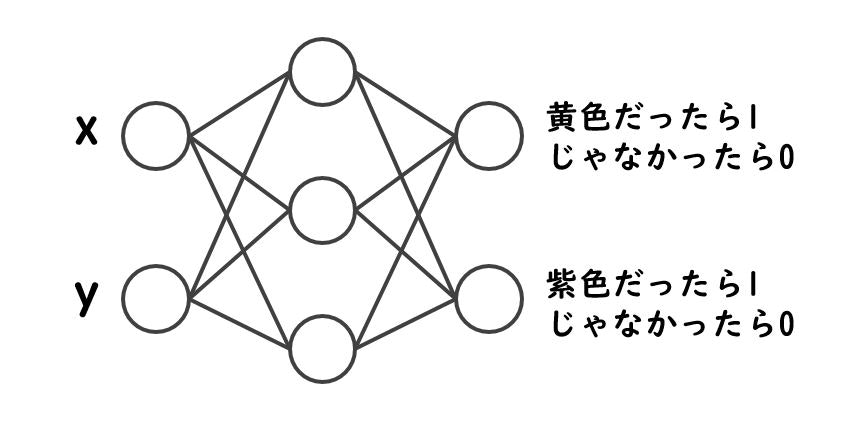
ニューラルネットワークとしてはこんな感じのものを作ります。
なんとなく隠れ層を１つ作ってみます。
例えば、 x=5 で y=15 とかだったら、たぶん紫色のほうが1になるようなモデルです。（上の散布図で (5,15) の場所を確認してみてください）

さっそくコードの説明

ライブラリのインポート

あ、言い忘れてましたが Python です。

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

これくらいで十分です。
tensorflowをtfとしてインポートしていますね。

テストデータの作成

本当はここはすでにあるデータをCSVなりで読み込んだりするのですが、今回はあくまでサンプルってことで自力で元データを作ります。

# テスト用にデータを生成する
# 2つのグループを作成、学習させて、(x,y)を与えたときにどちらかあてさせる

n = 100
n2 = 50

x0_data = np.random.rand(n2)*10
y0_data = np.random.rand(n2)*10 + 10
z0_data = np.zeros(n2)

x1_data = np.random.rand(n2)*10
y1_data = np.random.rand(n2)*10 + 30
z1_data = np.ones(n2)

x_data = np.concatenate([x0_data, x1_data])
y_data = np.concatenate([y0_data, y1_data])
z_data = np.concatenate([z0_data, z1_data])

# データを描画
plt.scatter(x_data, y_data, c=z_data)
plt.show()

# x_data に x と y と z をまとめる
x_data = np.c_[x_data, y_data]
z_data = np.c_[z_data==1, z_data==0]

ここはあくまでテストデータの作成だけで本質的な部分じゃないので作成部分の説明ははぶきます。 ただ、最終的にこういうデータになっているということは大事なので説明しておきます。

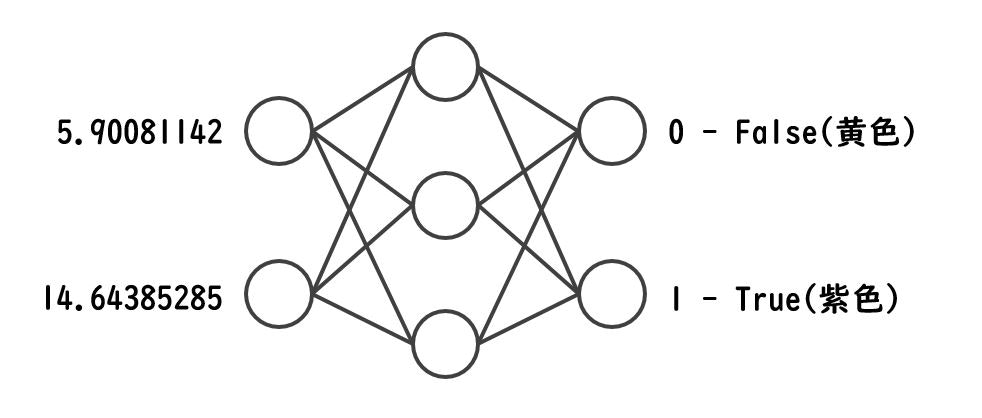
入力の学習データとなる x_data は、100行 2列 のテストデータです。 (x1,y1) (x2,y2)... の順に並んでます。

[[ 5.90081142 14.64385285]
 [ 3.83385081 13.43401696]
 [ 5.25889671 17.3863485 ]
       :
 [ 0.72534067 36.58296769]
 [ 7.91645831 35.65734696]
 [ 0.83942413 31.1661201 ]]

次に学習データのうち正解データとなる y_data は、100行 2列 のテストデータです。 (黄色,紫色)... の順に並んでます。

[[ False True]
 [ False True]
 [ False True]
       :
 [ True False]
 [ True False]
 [ True False]]

両方の1行目のデータをとってきてみると、こんな感じです。

こんな感じで100セット分のデータを準備しています。

ニューラルネットワークのモデルを作る

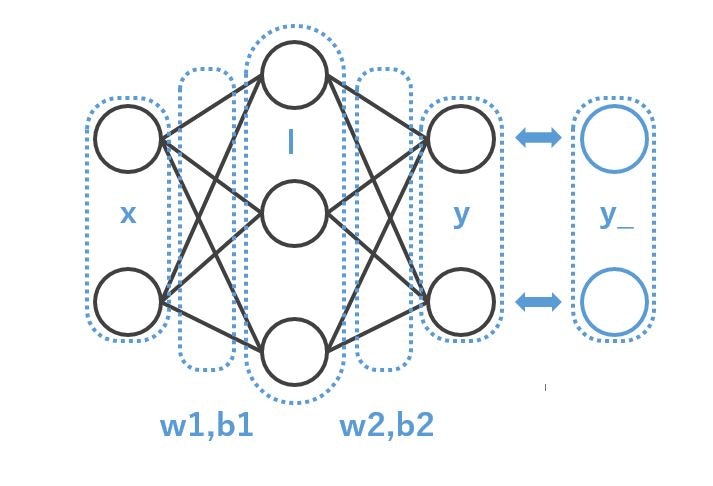
ここからが本題です。 まずはモデルを作ります。 ここでモデルとは 2-3-2 の形のネットワークです。 この段階ではあくまでモデル≒計算式を作ってるだけで実際の計算はまだ行われません。（なのでテストデータの x_data とかは出てきません）

## 入力層ノード 2 つを格納するプレースホルダ
x = tf.placeholder(tf.float32, [None,2])

## 出力層ノード 2 つを格納するプレースホルダ
y_ = tf.placeholder(tf.float32, [None,2])

## 重み と バイアス と 入力総和 - 入力が2 で 中間層側の出力が 3
w1 = tf.Variable(tf.random_normal([2,3]))
b1 = tf.Variable(tf.zeros(3))
l1 = tf.sigmoid(tf.matmul(x,w1) + b1)

## 重み と バイアス 中間層側の出力が 3 で 出力層側の出力が 2
w2 = tf.Variable(tf.random_normal([3,2]))
b2 = tf.Variable(tf.zeros(2))
y  = tf.matmul(l1,w2) + b2

イメージとしてはこんな感じです。

いくつかポイントだけ。

• 入力層 x が2つ。これはテストデータというか、x,y の2つのデータがインプットだというところが由来です
• 出力層 y が2つ。これはテストデータというか、黄色 or 紫色 がアウトプットだというところが由来です
• w1,b1 が tf.random_normal([2,3]) で作られていますが、これは、2-3-2 の 2→3 という構成のため。
• w2,b2 が tf.random_normal([3,2] で作られていますが、これは、2-3-2 の 3→2 という構成のため

このあたりの数の関係だけわかっていればとりあえずモデルは作れます。 入力データが増えるのであれば、x の数が増えて、かつ、w1,b1 の数も増えます。
（ちょっと図中のバイアスの位置がおかしい気もしますが…雰囲気ということで目をつぶってください）

誤差の定義

学習させるために、誤差の定義を行います。 クロスエントロピーとか言われるものたちです。

# 誤差の定義
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.arg_max(y_, 1), tf.argmax(y, 1)), tf.float32)) * 100.0
prediction = tf.nn.softmax(y)
summary = tf.summary.merge_all()

こまかな数式はいろいろケースにあわせて調整などするらしいですがおいておいて（すみません...説明できません＞＜）、ポイントとなるのは途中途中に出てくる y と y_ です。 モデルを通して y を計算させて、テストデータの y_ と比較して誤差を計算する計算式を定義しています。

トレーニングのステップの定義

# 学習用のOPの定義
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

誤差として定義した cross_entropy を最小にするようにと指示した train_step という処理を定義します。
ここまでがいわゆるモデルの作成で、これでやっと実際に計算（学習）できるところまで持ってきました。

やっと学習の開始

ついに学習します。

# ついに学習開始
sess = tf.Session()
sess.run(tf.global_variables_initializer())

print('Training...')

batch_size = 10
loop_per_epoch = int(len(x_data) / batch_size)

step = 0
for e in range(1000):
    for i in range(loop_per_epoch):
        batch_x = x_data[i*batch_size:(i+1)*batch_size-1]
        batch_y = z_data[i*batch_size:(i+1)*batch_size-1]
        _, loss, acc = sess.run([train_step, cross_entropy, accuracy], feed_dict={x:batch_x, y_:batch_y})
        step += batch_size

    if (e+1) % 100 == 0:
        print('epoch:{:3} loss:{:.6f} acc:{:6.2f}%'.format(e+1, loss, acc))

学習データは一気に食わせるのではなく何個ずつくわせるのが良いそうです。 今回は適当に batch_size = 10 として、10個ずつデータを使っていきます。

        batch_x = x_data[i*batch_size:(i+1)*batch_size-1]
        batch_y = z_data[i*batch_size:(i+1)*batch_size-1]

今回全部で100個のデータがあるので、100 / 10 の10回です。 for文でぐるぐる回しながら 0～9、10～19、20～29... と順番に x_data と y_data からデータをとってきて順次学習させます。

batch_xはこんな感じでデータを10個。

[[ 5.90081142 14.64385285]
 [ 3.83385081 13.43401696]
 [ 5.25889671 17.3863485 ]
       :

batch_yはこんな感じでデータを10個。

[[ False True]
 [ False True]
 [ False True]
       :

そして、

_, loss, acc = sess.run([train_step, cross_entropy, accuracy], feed_dict={x:batch_x, y_:batch_y})

として、feed_dict という変数のデータとして、x に batch_x を与えて、 y_ に batch_y を与えて、run して学習させます。 ここの x と y_ は最初にモデルとして作ったPlaceholderの x と y_ を指しています。 結果として、loss と acc をゲットしておきます。

    if (e+1) % 100 == 0:
        print('epoch:{:3} loss:{:.6f} acc:{:6.2f}%'.format(e+1, loss, acc))

ここもそんなに本質的な部分ではないですが、学習している感じを出したいので、100回に1回くらいログを出力しておきます。

とい感じで、適当に 1000回 くらいの学習を全体でさせています。

Training...
epoch:100 loss:0.237401 acc:100.00%
epoch:200 loss:0.204621 acc:100.00%
epoch:300 loss:0.175207 acc:100.00%
epoch:400 loss:0.146544 acc:100.00%
epoch:500 loss:0.120019 acc:100.00%
epoch:600 loss:0.100418 acc:100.00%
epoch:700 loss:0.082550 acc:100.00%
epoch:800 loss:0.065364 acc:100.00%
epoch:900 loss:0.050955 acc:100.00%
epoch:1000 loss:0.039824 acc:100.00%

loss で表現される誤差が減って言って、acc で表現されている正解率が上がっていけばOKです。 今回はあまりに簡単すぎるのか acc はすぐに 100% いってます。

とりあえずこれで学習モデルができました。

めでたしめでたし

最後にテスト！

学習させたモデルを使って実際にテストしてみましょう。

とってもシンプルに試してみます。

# テスト
test_input  = [[5,40],[1,1],[10,15]]
test_output = [[0,0],[0,0],[0,0]]

predict = sess.run(prediction, feed_dict={x:test_input,y_:test_output})

print(predict)

とりあえず3パターン [[5,40],[1,1],[10,15]] という適当なデータを与えてみます。 入力が2列なのは入力のノードが2つだからですね。 結果はこれから得るものなので何でもいいのでとりあえず同じ数の配列を用意しておきます [[0,0],[0,0],[0,0]] として変数だけ準備しておきます。 こちらも2列のデータなのは今回の出力のノードが2つだからです。

実行結果はこうなります。

[[0.8327447  0.16725525]
 [0.05283556 0.9471644 ]
 [0.06178974 0.93821025]]

本当はこの数値も関数を通して 1 か 0 にした方するべきなのでしょうが、とりあえず計算結果を生の数字で見ると上になります。 これを整理してみるとこういう感じの意味です。

 [ 5,40] -> [ 0.83.., 0.16.. ] -> [ 1, 0 ] = 黄色グループ
 [ 1, 1] -> [ 0.05.., 0.94.. ] -> [ 0, 1 ] = 紫色グループ
 [10,15] -> [ 0.06.., 0.93.. ] -> [ 0, 1 ] = 紫色グループ

散布図でそれぞれの位置を見比べてみて、、、あってそうですね？
(5,40)は黄色の場所っぽいし、(1,1)は紫の場所っぽい。

これで見事にモデルを作って、学習して、適当なデータを与えて見事に正解をあてました。

さて実際に使う場合には？

ここで終わるとまた路頭に迷うと思うので次のヒント。

• 自分たちが学習させたいデータの数、得たい結果に応じて、モデルを考える。 具体的には、入力 と 出力 の丸の数を考えます。
• 適当に隠れ層とかを考える
• それに応じてモデルを作る、実際には TensorFlowのモデルのテンソル≒ベクトル≒配列の形を決める
• 手持ちのデータを食わせて学習する
• まじめにNNの勉強をしてクロスエントロピーやらをより正しい式におきかえる

という感じかと思います。

さいごに

わたしは数学者ではなくてプログラマなので、プログラム組んで動かして、式を変えて動かして、数字を変えて動かして、をしていきたいので、わたし自身これをベースに Try & Error でがんばって勉強していきます。

ですが、とりあえず動いて、とりあえずそれっぽい答えが出た自分をほめてあげたい。

お願い

特にクロスエントロピーやらそのあたりは、あまり理解がおいついてないので…… 編集リクエストお願いいたします。
もし何か１つでも役にたったことがあったら、いいね よろしお願いします！

全コード

今回のコードはこちらになります。

import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

# テスト用にデータを生成する
# 2つのグループを作成、学習させて、(x,y)を与えたときにどちらかあてさせる

n = 100
n2 = 50

x0_data = np.random.rand(n2)*10
y0_data = np.random.rand(n2)*10 + 10
z0_data = np.zeros(n2)

x1_data = np.random.rand(n2)*10
y1_data = np.random.rand(n2)*10 + 30
z1_data = np.ones(n2)

x_data = np.concatenate([x0_data, x1_data])
y_data = np.concatenate([y0_data, y1_data])
z_data = np.concatenate([z0_data, z1_data])

# データを描画
plt.scatter(x_data, y_data, c=z_data)
plt.show()

# x_data に x と y と z をまとめる
x_data = np.c_[x_data, y_data]
z_data = np.c_[z_data==1, z_data==0]

####################################################
# 入力層のノードが 2 つ (x と y)
# 中間層が1つでノードが 3 つ
# 出力層のノードが 2 つ（第1グループ か 第2グループ か）
# 2 - 3 - 2 の構成
####################################################
####################################################
# モデル作成
## 入力層ノード 2 つを格納するプレースホルダ
x = tf.placeholder(tf.float32, [None,2])

## 出力層ノード 2 つを格納するプレースホルダ
y_ = tf.placeholder(tf.float32, [None,2])

## 重み と バイアス と 入力総和 - 入力が2 で 中間層側の出力が 3
w1 = tf.Variable(tf.random_normal([2,3]))
b1 = tf.Variable(tf.zeros(3))
l1 = tf.sigmoid(tf.matmul(x,w1) + b1)

## 重み と バイアス 中間層側の出力が 3 で 出力層側の出力が 2
w2 = tf.Variable(tf.random_normal([3,2]))
b2 = tf.Variable(tf.zeros(2))
y  = tf.matmul(l1,w2) + b2


####################################################
# 誤差の定義
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y))
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.arg_max(y_, 1), tf.argmax(y, 1)), tf.float32)) * 100.0
prediction = tf.nn.softmax(y)

summary = tf.summary.merge_all()

####################################################
# 学習用のOPの定義
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

####################################################
# ついに学習開始
sess = tf.Session()
sess.run(tf.global_variables_initializer())

print('Training...')

batch_size = 10
loop_per_epoch = int(len(x_data) / batch_size)

step = 0
for e in range(1000):
    for i in range(loop_per_epoch):
        batch_x = x_data[i*batch_size:(i+1)*batch_size]
        batch_y = z_data[i*batch_size:(i+1)*batch_size]
        _, loss, acc = sess.run([train_step, cross_entropy, accuracy], feed_dict={x:batch_x, y_:batch_y})
        step += batch_size

    if (e+1) % 100 == 0:
        print('epoch:{:3} loss:{:.6f} acc:{:6.2f}%'.format(e+1, loss, acc))

####################################################
# テスト
test_input  = [[5,40],[1,1],[10,15]]
test_output = [[0,0],[0,0],[0,0]]

predict = sess.run(prediction, feed_dict={x:test_input,y_:test_output})

print(predict)