前回sin関数をchainerを使って近似しようとしてみたのだが、うまくいかなかったためいろいろ可視化しながら再チャレンジしてみた。結論から言うと失敗に終わった。なぜなのか未だにわからない(局所解に陥ったか気がするのだが・・・・)。ご指摘していただけるとすごくありがたい。
前回と異なる点
-sin(x)ではなくsin(0.25x)の近似を目標とした
-yの値を出力させてみた
-損失平均のグラフを出力した
import numpy as np
import six
import chainer
from chainer import computational_graph as c
from chainer import cuda
import chainer.functions as F
from chainer import optimizers
import matplotlib.pyplot as plt
import csv
def make_dateset():
x_train = np.arange(0,3.14*40.0,0.5)
y_train = np.sin(0.25 * x_train).astype(np.float32)
f = open('sin_train.csv','ab')
csvWriter = csv.writer(f)
csvWriter.writerow(x_train)
csvWriter.writerow(y_train)
f.close()
x_test = np.arange(3.14*40.0,3.14 * 60.0,0.5)
y_test = np.sin(0.25 * x_test).astype(np.float32)
return x_train.astype(np.float32),y_train.astype(np.float32),x_test.astype(np.float32),y_test.astype(np.float32)
def forward(x_data,y_data,train = True,pred_flag = False):
if pred_flag:
x = chainer.Variable(x_data)
train = False
else:
x,t = chainer.Variable(x_data),chainer.Variable(y_data)
h1 = F.dropout(F.relu(model.l1(x)), train=train)
h2 = F.dropout(F.relu(model.l2(h1)), train=train)
h3 = F.dropout(F.relu(model.l3(h2)), train=train)
y = model.l4(h3)
if pred_flag:
return y
else:
return F.mean_squared_error(y,t)
if __name__ == "__main__":
x_train,y_train,x_test,y_test = make_dateset()
x_train = x_train.reshape(len(x_train),1)
y_train = y_train.reshape(len(y_train),1)
x_test = x_test.reshape(len(x_test),1)
y_test = y_test.reshape(len(y_test),1)
xp = np
batchsize = 20
N = len(x_train)
N_test = len(x_test)
n_epoch = 500
n_units = 10
model = chainer.FunctionSet(l1=F.Linear(1, n_units),
l2=F.Linear(n_units, n_units),
l3=F.Linear(n_units, n_units),
l4=F.Linear(n_units, 1))
optimizer = optimizers.Adam()
optimizer.setup(model.collect_parameters())
loss_means = []
for epoch in six.moves.range(1, n_epoch + 1):
print('epoch', epoch)
#train
perm = np.random.permutation(N)
sum_loss = 0
sum_accuracy = 0
for i in six.moves.range(0, N, batchsize):
x_batch = xp.asarray(x_train[perm[i:i + batchsize]])
y_batch = xp.asarray(y_train[perm[i:i + batchsize]])
optimizer.zero_grads()
loss = forward(x_batch, y_batch)
loss.backward()
optimizer.update()
sum_loss += float(cuda.to_cpu(loss.data)) * len(y_batch)
print "train mean loss = ",sum_loss/N
#evaluation
sum_loss = 0
sum_accuracy = 0
for i in six.moves.range(0, N_test, batchsize):
x_batch = xp.asarray(x_test[i:i+batchsize])
y_batch = xp.asarray(y_test[i:i+batchsize])
loss = forward(x_batch, y_batch, train=False)
sum_loss += float(cuda.to_cpu(loss.data)) * len(y_batch)
###################################################
if epoch == 200:
#predictデータを作成
x_pre = np.arange(3.14*80.0,3.14*120.0,0.5)
x_pre = x_pre.astype(np.float32)
y_pre = np.sin(0.25 * x_pre).astype(np.float32)
y_pre = y_pre.reshape(1,len(y_pre))
answer = []
#predict
for g in range(0,len(x_pre)-1):
xx = np.asarray([[x_pre[g]]])
y1 = forward(x_data = xx,y_data = None,train = False,pred_flag=True)
answer.append(y1.data[0][0])
f = open('sin_pre.csv','ab')
csvWriter = csv.writer(f)
csvWriter.writerow(x_pre)
csvWriter.writerow(y_pre[0])
csvWriter.writerow(answer)
f.close()
####################
print "test mean loss = ",sum_loss/N_test
loss_means.append(sum_loss/N_test)
f = open('loss_means.csv','ab')
csvWriter = csv.writer(f)
csvWriter.writerow(loss_means)
f.close()
-Deep Learningのパラメーター
ミニバッチサイズ 20
epoch数(学習回数) 500
ユニット数 1-20-20-1
活性化関数 ReLu(正規化線形関数)
更新方法 Adam
損失誤差関数 平均二乗誤差関数
学習データ
まず今回学習させるデータ(train data)をプロットしてみた
y=sin(0.25x)
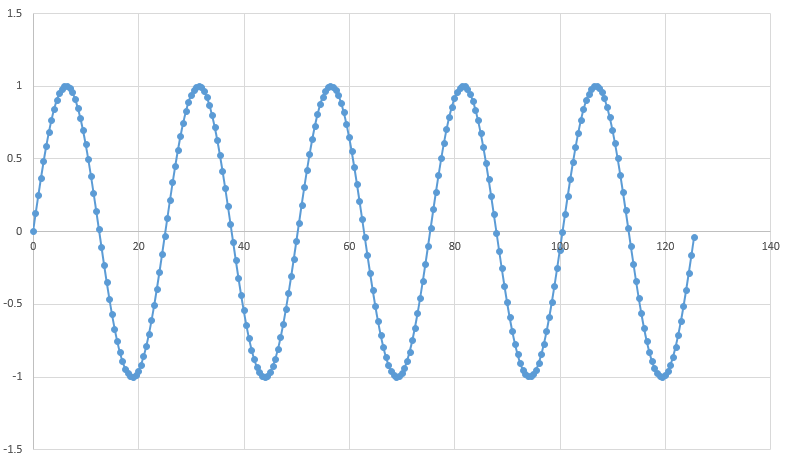
0<x<3.14*40の範囲で0.5ずつ訓練データとして作成
テストデータは3.14*40.0<x<60.0の範囲で0.5間隔で作成した
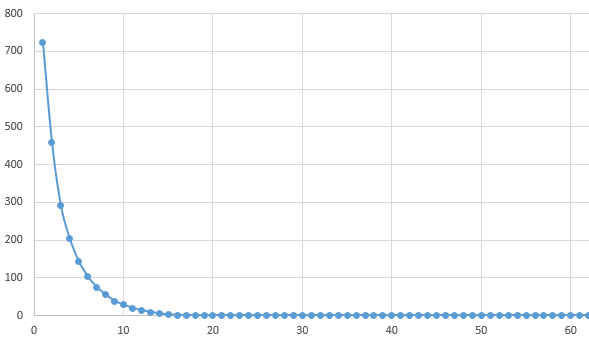
損失平均グラフ
sin関数の近似があまりにもできないので確認のためにプロットしてみた。最初の損失平均値が大きすぎてepoch13あたりから0になっているように見えるが実際は0.5付近をうろうろしている。0.5まで減少するのだが、そこから全く減少しない。バッチ数・ユニット数を変えても0.5付近で減少が止まってしまった。
予想グラフ
実際にどのような関数になるか出力してみた。epochが200時
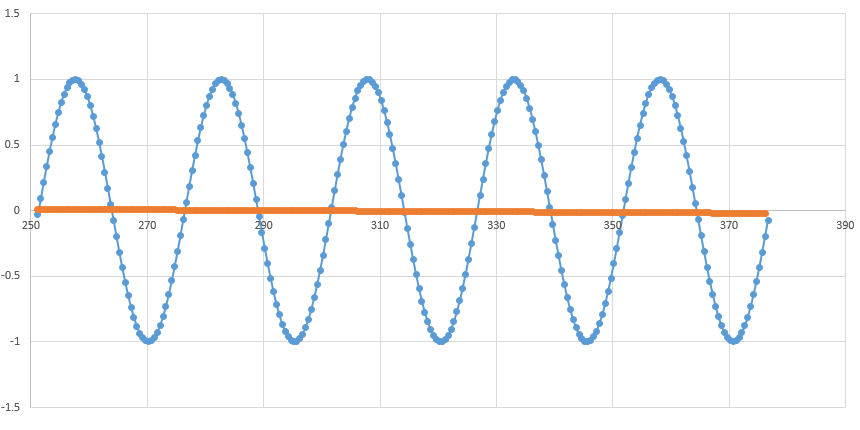
青が正解(本来の0.25*sin(x)関数)、オレンジがDeep Learningの出力関数。まあこれなら損失平均も0.5になるわなって感じです。局所解に陥ってしまった場合の解決方法としては学習率をいじればよかった気がするんだけどまだまだ勉強中なのでどうすればいいのか・・・・・
どなたか助けてください(笑)