Caution
記事中で符号なし整数の演算結果が負になる場合の挙動をUBとして紹介していますが、定義された動作でした。
N4318の
As can be seen, per the standard the negative result wraps around from the maximum positive value for the simple minus operation
の文章ちゃんと読んで、執筆時の私・・・
はじめに
最近、ツイッターを見ていると、プログラマの間でnull安全という言葉がバズっていますね。私も次のようなエントリを楽しく眺めていた訳です:
さてそんな中、少しだけ私の心に留まったエントリがこれです:
何ていうことが書かれている
コンパイラのリミッタが外れつつある今、null安全は必須なのかもしれない
記事を見かけました。確かに、null安全という言葉がバズっていますなぁ。
C/C++におけるnull安全が必要な理由はなにか
コンパイラのリミッタが外れつつある今、null安全は必須なのかもしれない
コンパイラが斜め上の最適化をするようになったからnull安全ないと怖いよね
この一言に尽きます。が、そもそもなぜ斜め上の最適化をするのでしょうか?
いろいろあるけどundefined behaviorを踏んでいるからじゃね?
おなじみ本の虫の記事です。C++erなら当然すでに読んでいると思います。
もっとも注目されるundefined behaviorはNULL Pointer Dereferenceです(当社比)
ここまで見てきたリンク先も口酸っぱく注意を発しています。
undefined behaviorとは
規格上一般人には理解不能な言葉がどっさりあるので頭を整理してから読み進めることにしましょう。
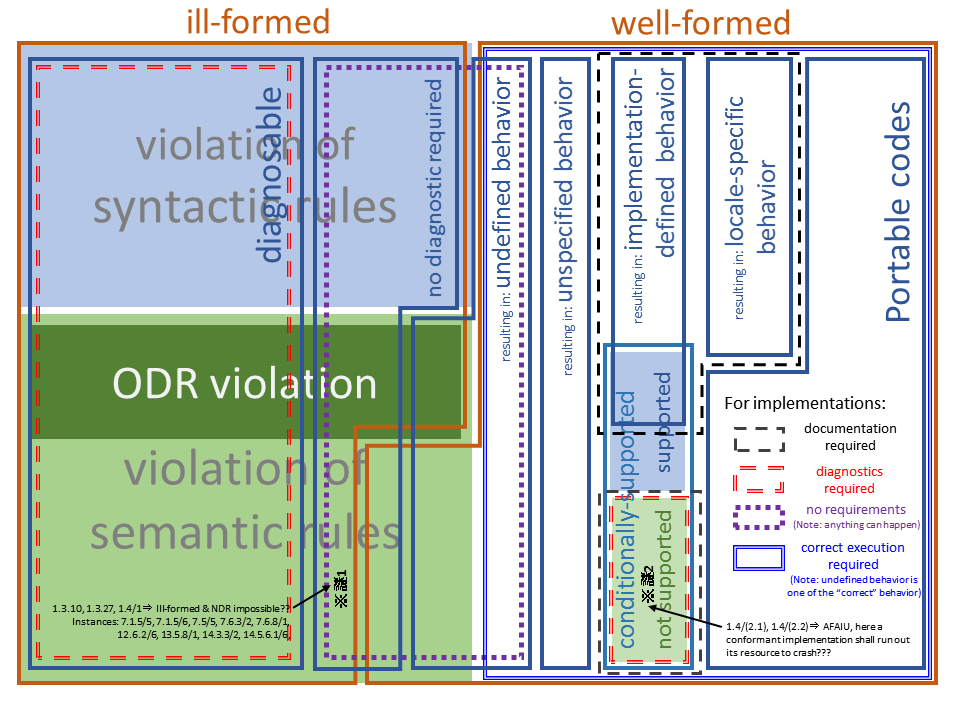
下図は私が作ったわけではなく、C++の会のSlackで @akinomyoga さんが作られたものです。
これの詳細についてはそのうち誰かが詳しく書いてくれるのを信じて(Advent Calendarとか)そこに丸投げします。まあまだ若干解釈に揺れがあるようですが。
追記:
なんと @akinomyoga さんががっつり記事を書いてくれた。
C++er は“合法”だとか“違法”だとか言いたくて仕方がないけれど、結局どういう意味? それより適合・適格・○○動作・○○規則・診断不要いろいろの関係が謎 - Qiita
http://qiita.com/akinomyoga/items/592e5a3b8438a0c8556b
もっと身近なundefined behavior=四則演算
しかし、なにもNULL Pointer Dereferenceだけがundefined behaviorなわけではありません。
例えばこんなコードを見てみましょう。
#include <iostream>
#include <cmath>
int main() {
unsigned int three = 3;
unsigned int five = 5;
std::cout << "The difference between three and five is ";
std::cout << three - five << std::endl;
std::cout << "The absolute value of that difference is ";
std::cout << abs( three - five ) << std::endl;
return 0;
}
The difference between three and five is 4294967294
The absolute value of that difference is 4.29497e+09
このコードは数学的に書けば
|a - b|
ですね。しかしプログラミング言語においては、無限精度整数型でもない限り、表せる範囲が決まっているため、期待している2ではなくこのような結果になってしまいます。
ふふ~ん、じゃあN4318のabs_diffを使えばいいんでしょ?
というわけで
[PDF] N4318: Proposal to add an absolute difference function to the C++ Standard Library
が提案されています。
つまり
template <typename T>
decltype(auto) std::abs_diff( const T& a, const T& b )
{
if (a<b) return b-a; return a-b;
}
template <typename T, typename Compare>
decltype(auto) std::abs_diff( const T& a, const T& b, const Compare& comp )
{
if (comp(a,b)) return b-a; return a-b;
}
template <typename T, typename Compare, typename Difference>
decltype(auto) std::abs_diff( const T& a, const T& b, const Compare& comp, const Difference& diff )
{
if (comp(a,b)) return diff(b,a); return diff(a,b);
}
こういうラッパーです。
#include <iostream>
#include <cmath>
int main() {
unsigned int three = 3;
unsigned int five = 5;
std::cout << std::abs_diff(three, five) << std::endl;
return 0;
}
2
じゃあこんなコードはどうでしょう?
#include <iostream>
#include <limits>
int main() {
using lim = std::numeric_limits<int>;
std::cout << std::abs_diff(lim::min(), 15) << std::endl;
return 0;
}
わかりやすさのために展開してみましょう。
#include <iostream>
#include <limits>
int main() {
using lim = std::numeric_limits<int>;
std::cout << (15 - lim::min()) << std::endl;
return 0;
}
これはだめですね。オーバーフローしてしまっています。これは Undefined Behaviorです。
つまり安全に差の絶対値を計算できるようにはどうすればいいのか
まず絶対条件として絶対値の差はunsigned な型であるべきです。計算結果が格納できなくなるケースが激減します。
で、これを実現するためのコードがこちらです。長いですがあえて載せます。
#include <limits>
#include <type_traits>
#include <stdexcept>
namespace math {
namespace detail {
constexpr bool is_two_s_complement() noexcept {
return std::numeric_limits<int>::min() + 1 == -std::numeric_limits<int>::max();
}
constexpr bool is_one_s_complement_like() noexcept {
return std::numeric_limits<int>::min() == -std::numeric_limits<int>::max();
}
constexpr bool abs_diff_both_signed_can_noexcept() noexcept {
return is_two_s_complement() || is_one_s_complement_like();
}
/**
* @param a bigger unsigned num
* @param b smaller signed negative num
*/
template <typename T1, typename T2, std::enable_if_t<
std::is_unsigned<T1>::value && std::is_signed<T2>::value,
std::nullptr_t
> = nullptr>
static inline constexpr auto abs_diff_impl(const T1& a, const T2& b)
->std::make_unsigned_t<std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, T1>>
{
using lim = std::numeric_limits<T2>;
using utype = std::make_unsigned_t<std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, T1>>;
using ulim = std::numeric_limits<utype>;
//prevent overflow
//http://qiita.com/a4lg/items/bc4d2cfbce22fe749589
//-std::numeric_limits<T>::min() < std::numeric_limits<T>::max() : iregal after C99
//std::numeric_limits<T>::min() < -std::numeric_limits<T>::max() : most familiar behavior
//std::numeric_limits<T>::min() = -std::numeric_limits<T>::max() : possible
//note: 0 <= a, b < 0
// |<------------b-------------->|
//lim::min() -lim::max() 0 a lim::max()
// | | | | |
//----+-------------+-----.......---+------.......-----+----.......-----+-----
return (-lim::max() <= b)
//note: ``-b`` is no problem
//lim::min() -lim::max() b 0
// | | | |
//----+-------------+-----.......---+------.......-----+----.......
? (static_cast<utype>(-b) <= (ulim::max() - a))
//can store
? static_cast<utype>(a) + static_cast<utype>(-b)
//There is no possibility when ``a`` is signed number before a was passed to this fuction.
: throw std::invalid_argument("cannot store result.")
//note: std::numeric_limits<T>::min() <= b < -std::numeric_limits<T>::max()
//lim::min() b -lim::max() 0
// | | | |
//----+-------------+-----.......---+------.......-----+----.......
:
(
(static_cast<utype>(lim::max()) < (ulim::max() - static_cast<utype>(a)))
// (---------try to store rest---------) (----------------storable max num----------------)
&& (static_cast<utype>((-lim::max()) - b) <= (ulim::max() - lim::max() - static_cast<utype>(a)))
)
//can store
? static_cast<utype>(a) + static_cast<utype>(lim::max()) + static_cast<utype>((-lim::max()) - b)
//when processing system doesn't use two's complement and
//std::numeric_limits<T>::min() < -std::numeric_limits<T>::max(),
//or
//a, before pass to this function, is unsigned and type of a is utype,
//there is possibility no way to store result.
//In that case, we throw exception.
: throw std::invalid_argument("cannot store result.");
}
}
template <typename T1, typename T2, std::enable_if_t<
std::is_unsigned<T1>::value && std::is_signed<T2>::value,
std::nullptr_t
> = nullptr>
static inline constexpr auto abs_diff(const T1& a, const T2& b)
->std::conditional_t<(sizeof(T1) < sizeof(T2)), std::make_unsigned_t<T2>, T1>
{
return (0 < b && a < static_cast<std::make_unsigned_t<T2>>(b))
? static_cast<std::make_unsigned_t<T2>>(b) - a
: (0 <= b)
? a - static_cast<std::make_unsigned_t<T2>>(b)
//b < 0
: detail::abs_diff_impl(a, b);
}
template <typename T1, typename T2, std::enable_if_t<
std::is_signed<T1>::value && std::is_unsigned<T2>::value,
std::nullptr_t
> = nullptr>
static inline constexpr auto abs_diff(const T1& a, const T2& b)
->std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, std::make_unsigned_t<T1>>
{
return abs_diff(b, a);
}
template <typename T1, typename T2, std::enable_if_t<
std::is_unsigned<T1>::value && std::is_unsigned<T2>::value,
std::nullptr_t
> = nullptr>
static inline constexpr auto abs_diff(const T1& a, const T2& b) noexcept
->std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, T1>
{
return (a < b) ? b - a : a - b;
}
template <typename T1, typename T2, std::enable_if_t<
std::is_signed<T1>::value && std::is_signed<T2>::value,
std::nullptr_t
> = nullptr>
static inline constexpr auto abs_diff(const T1& a, const T2& b) noexcept(detail::abs_diff_both_signed_can_noexcept())
->std::make_unsigned_t<std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, T1>>
{
using bigger_type = std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, T1>;
using lim = std::numeric_limits<bigger_type>;
using utype = std::make_unsigned_t<bigger_type>;
return (b < a)
? abs_diff(b, a)
//a <= b
: (0 <= a)
// 0 <= a <= b
? abs_diff(static_cast<utype>(a), static_cast<utype>(b))
//a <= b, a < 0
: (0 < b)
//a < 0 < b
? detail::abs_diff_impl(static_cast<utype>(b), a)
//a <= b <= 0
: (-lim::max() <= a || b <= -(-lim::max() - lim::min()))
//-lim::max() <= a <= b <= -(-lim::max() - lim::min())
? static_cast<utype>(b - a)
// lim::min() <= a < -lim::max(), -(-lim::max() - lim::min()) < b <= 0
: static_cast<utype>(-(a + lim::max())) + static_cast<utype>(b + lim::max());
}
}
-
signedとsigned -
signedとunsigned -
unsignedとsigned -
unsignedとunsigned
の計4パターンについてそれぞれ関数をオーバーロードさせています。
signedとunsignedが混ざっている2パターンと
処理系がstd::numeric_limits<T>::min() + 1 < -std::numeric_limits<T>::max()となる場合、格納できない場合があるので例外を投げています。
つまり、C/C++において、安全に絶対値の差を計算するには毎度この100行超えのコードを書く必要があります。
あなた、騙されていますよ?
はい、安全に絶対値の差を計算するのに100行超えのコードを書くなんて馬鹿げてます。もう一度先のコードを見てみましょう。
template <typename T1, typename T2, std::enable_if_t<
std::is_unsigned<T1>::value && std::is_unsigned<T2>::value,
std::nullptr_t
> = nullptr>
static inline constexpr auto abs_diff(const T1& a, const T2& b) noexcept
->std::conditional_t<(sizeof(T1) < sizeof(T2)), T2, T1>
{
return (a < b) ? b - a : a - b;
}
ついでにN4318提案のコードも見てみましょう
template <typename T>
decltype(auto) std::abs_diff( const T& a, const T& b )
{
if (a<b) return b-a; return a-b;
}
つまり、unsigned同士での差の絶対値は容易に安全に求められるわけです。
結論
- 一応100行を超えるコードを書けば安全に差の絶対値を計算することはできる
unsigned同士での差の絶対値は容易に安全に求められる
→ 積極的にunsignedな整数型を使おう
unsignedな整数型はいいぞ、bit演算もできるし。signedな整数型はbit演算してはいけないですからねぇ。
Googleのコーディング規約は
for (unsigned int i = foo.Length()-1; i >= 0; --i)
こういうコードが無限ループするからつかうなとか言ってますが、これに警告を出せないコンパイラを投げ捨てればいいだけで、そのためにsignedな整数型をつかうなんで馬鹿げてます。
signed と unsigned を比較するときにも同じくらいひどいバグを引き起こすおそれが
とかいうことも言ってますが、それはsigned/unsignedどっちの整数型を使うか以前の問題ですからね。しかもこれまたこれに警告を出せないコンパイラを投げ捨てればいいだけです。Visual Studioでも/W4をつければ教えてくれます。
ところでこの記事を書くにあたりお世話になった記事
- C++ における整数型の怪と "移植性のある" オーバーフローチェッカー (第1回 : 整数型の怪と対策の不足)
- C++ における整数型の怪と "移植性のある" オーバーフローチェッカー (第2回 : 符号無し整数型のチェック)
- C++ における整数型の怪と "移植性のある" オーバーフローチェッカー (第3回 : C言語の整数の性質を知る)
- C++ における整数型の怪と "移植性のある" オーバーフローチェッカー (第4回 : 符号付き整数型のチェックと動機の動機)
- C++ における整数型の怪と "移植性のある" オーバーフローチェッカー (第5回 : 続・符号付き整数型のチェック)
Coqをもちいて、C/C++の整数演算が安全な条件を求め証明していくという頭のおかしい素晴らしい試みをしている記事があります(第6回お待ちしています!)。これのお陰でどうにか頭がこんがらがらずに一応それらしいコードを書くことができました。
上記の記事にもあるように、
整数オーバーフローは、特に C/C++ においては深刻な脆弱性の原因になりがちです。昨年界隈を騒がせた Android の Stagefright としてくくられている複数の脆弱性のうち大部分は、この整数オーバーフローが原因となっています。
整数演算はちょっとしたことで整数オーバーフローをやらかしてしまいがちです。そしてそれらは、深刻な脆弱性の原因になったり、コンパイラが思いもよらないコードを吐く原因になります。
余談
この記事を書いている最中で @yohhoy さんに先を越されたんですよね・・・。
鼻から悪魔:不定値(indeterminate value)バージョン
C/C++においてnull安全が求められる理由の一つはnull pointer dereferenceという名のundefined behaviorをやらかすかもしれないからだけど、undefined behaviorはなにもnull pointer dereferenceだけじゃねーぞってことが書いてあるという意味で。
資料
100行超えの上記コードは
これのテストコードは
です。
追記
似たような話として、安全にsignedな整数とunsignedな整数を比較できない問題について、標準ライブラリでどうにかしようという提案が出ています
P0586R0: Safe integral comparisons
解説: https://cpplover.blogspot.jp/2017/11/c-p0586r0-p0649r0.html