スタンフォード大学の"Deep Learning for Natural Language Processing"という授業の映像とスライドが公開されているので最近視聴しているのですが、観ただけだと身に残らなさそうなので内容を要約しつつ講義メモを公開することにしました。
今回は第2回目"Simple Word Vector representations: word2vec, GloVe"です。1回目はイントロなので飛ばしました。
単語毎に意味を表現する方法とその問題点
単語の意味をコンピュータに認識させたい場合、WordNetなどの人手で作られた分類表を使う方法がある。しかしこうした表現には問題がある。
- 細かいニュアンスを表現されていない(adept, expert, good, practiced, proficient, skillfulなどのsynonymsの違いとか)
- 新しい単語に対応しきれない
- 主観的である
- 人間が頑張らないといけない
- 正確な単語類似度を計算することが難しい
という訳で単語毎に意味を表現しようとするのはあまり上手くいかない。
分布類似度に着目する: 単語共起行列
単語の言語学的な意味ではなく、文書集合中で周りに出現している単語の分布によって単語の類似度を考えることができる。これは現代の統計的NLPで最も成功しているアイデアの1つ。
例えば"banking"という単語が出現する2つの文章があるとして
このオレンジで塗られている部分の単語が"banking"を表していると考える。
このモデルをコンピュータで扱えるようにするには、単語間の共起関係を行列で表現すればいい。オレンジの部分の大きさを文書全体にするのか、それとも前後N文字までという風にするのか(この範囲をウィンドウと言ったりする)というオプションがあって、ウィンドウを設けることで、単語が文書中で出現した位置とか意味を考慮させることができると言える。ウィンドウの大きさは一般的に5から10にすることが多い。単語の左と右で重みを変えたり、単語に遠さに応じて重み付けすることもできる。
単語共起行列の例
- I like deep learning.
- I like NLP.
- I enjoy flying.
という文書をコーパスにして、ウィンドウサイズを1、単語の左右で重みを同じにしたときの共起行列はこうなる:
単語共起行列の問題点
- 出現する単語に応じて次元数が増えていくのでコーパスが大きくなると巨大で疎な行列になる
- 次元数が増えると工夫しないと大量のストレージ容量が必要になったりもする
要するに頑健性に乏しい。
これらの問題に対する基本的なアイデアは、なんでもかんでも行列にするのではなくて、重要な情報だけを抜き出すことで小さくて密にするということ。一般的には25から1000次元くらいに圧縮したい。ではどうやってそれをやるか?
単語共起行列を密にする
いくつかの方法が提案されている。ここではSVD, word2vec, GloVeを取り上げる。
SVD
行列の特異値分解(SVD)を行う方法がまずある。SVDはnumpyに実装されているので試すことができる。
import numpy as np
la = np.linalg
words = ["I", "like", "enjoy", "deep",
"learning", "NLP", "flying", "."]
# ↑の単語共起行列を頑張って手入力したもの
X = np.array([
[0,2,1,0,0,0,0,0],
[2,0,0,1,0,1,0,0],
[1,0,0,0,0,0,1,0],
[0,1,0,0,1,0,0,0],
[0,0,0,1,0,0,0,1],
[0,1,0,0,0,0,0,1],
[0,0,1,0,0,0,0,1],
[0,0,0,0,1,1,1,0]
])
# SVD
U, s, Vh = la.svd(X, full_matrices=False)
これによって元々疎だった単語共起ベクトルが密になる。例えば "deep" という単語の場合
>>> print(X[3])
[0 1 0 0 1 0 0 0]
だったのが
>>> print(U[3])
[ -2.56274005e-01 2.74017533e-01 1.59810848e-01 -2.77555756e-16
-5.78984617e-01 6.36550929e-01 8.88178420e-16 -3.05414877e-01]
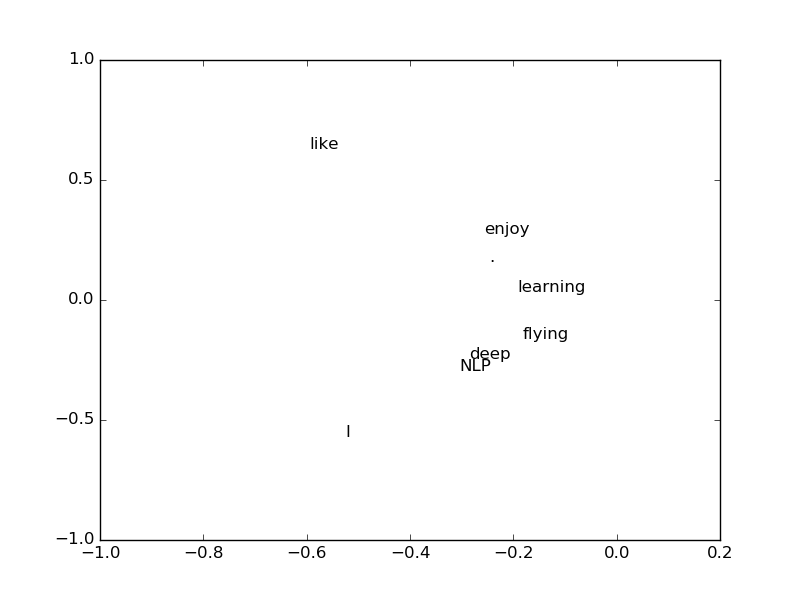
になる。これだけだと何がなんやらという感じだけど、0番目と1番目の次元だけを取ってきて各単語を2次元空間にプロットしてみると、なんとなく "deep" と "NLP" が近かったり、 "enjoy" と "learning" が近かったりとそれっぽく分類できているように見える。
SVDの中身
ところでSVDを使うことの妥当性については講義で触れられていなかった気がする。"Latent Semantic Analysis"について言及していたから、そっちを見ろということなのかも知れない。
SVDを使うと、ランクが $r$ である $n \times n$行列 $X$ は、 $n \times r$ の列直交行列 $U$ と $V$、対角要素に $D$ の特異値を並べた $r \times r$ 行列 $S$ を用いて次のように分解することができる。
X = U S V^T
このとき $S V^T$ を $W$ と置くと
X = U W
になる。$X$ というのはなんかの行列 $W$ を $U$ で変換したものだと言える。ところで $U$ は列直行行列なので列ベクトルは互いに独立している。つまり何かの空間の基底になっているのだけど、実はこれが単語空間になっていて、各列ベクトルが潜在的意味を表すと考えることができる。
SVDの問題点
SVDは一般化して $n \times m$行列にも適用することができる。仮に$n < m$だったとすると、そういった行列から計算するのに掛かる計算コストが $O(mn^2)$ なので巨大が行列には適用できない。そんな訳で新しい単語が出てきた時に組み込むことが大変。
word2vec
いろいろな手法が提案されているが、2013年にGoogleのMikolovらが提案したword2vecが注目されている。
word2vecのアイディアは「共起回数を直接扱うのではなく、周辺に出現する単語を確率的に扱う」というもの。より高速で、新しい単語を追加することが容易になっている。
word2vecもC言語、Java、Pythonでの実装があるので試すことができる。
理論
各単語の前後に大きさcのウィンドウを考えて、ウィンドウ内の各単語に対して、そこにそれが出現する確率を考え、それを足し合わせたものを目的関数にして、最尤推定する。対数を取っているのは、後で計算しやすくするため。
J(\theta) = \frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c,j \neq 0} \log p(w_{t+j} | w_t)
ベクトルの関係
word2vecを使うと単語はベクトルとして表現される。このとき、単語ベクトル間の差から興味深い結果が得られることが知られている。
例えば King から Man を引いて Woman を足すと Queen のベクトルと非常に近くなる、など。これは King から Man を引いてできるベクトルが、何か権力的な概念を表していると考えることができる。
X_{king} - X_{man} + X_{woman} \approx X_{queen}
日本語のコーパスをmecabで解析して同じようなことをしたら、グーグルからヤフーを引いてトヨタを足したら日産になった、というような話もあるようだ。
速度
word2vecは巨大なコーパスに対しても高速に学習可能とのこと。日本語のWikipedia文書をbz2圧縮された2GB程度のコーパスを、30分程度の時間で学習できたそうな。
昔GenSimを使って同様に日本語WikipediaでLDAをしてみたことがあるが、その時は半日がかりだった記憶がある。C言語で実装されていること、マシンスペックが当時より上がっていることを差し引いても、word2vecの方が圧倒的に高速であることは間違い無さそうだ。
GloVe
SVD的な単語の出現回数に基づく方法と、word2vec的な確率的に扱うアプローチがあることを見てきたが、それぞれ互いに長所と短所がある。
- 出現回数に基づく方法
- 小さなコーパスなら高速に学習できるが、大きくなると時間がかかる。
- 単語の類似度を測るのに使われるが、出現回数が少ない単語が不釣り合いなほど大きな重要性を得ることがある。
- 確率に基づく方法
- 大きなコーパスでないといけない。
- 単語類似度以外の複雑なパターンも計測することができる。
2つの世界を組み合わせていいとこどりするGloVeという方法が(この講義を担当しているRichard Socher氏らのグループによって)提案されている。
- 学習が速く
- 大きなコーパスに対応可能で
- 小さなコーパス、小さなベクトルでもパフォーマンスがいい