ロジスティック回帰とは
線形回帰と似ているが、目的変数が2値のときに利用する。
例えば、この人は商品を購入するか否か、棒に当たるか否か、引っ越すか否か、転職するか否かなどなど。
予測モデルを、以下のロジスティック関数(シグモイド関数)を使って作成。
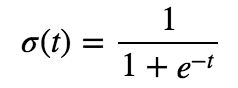
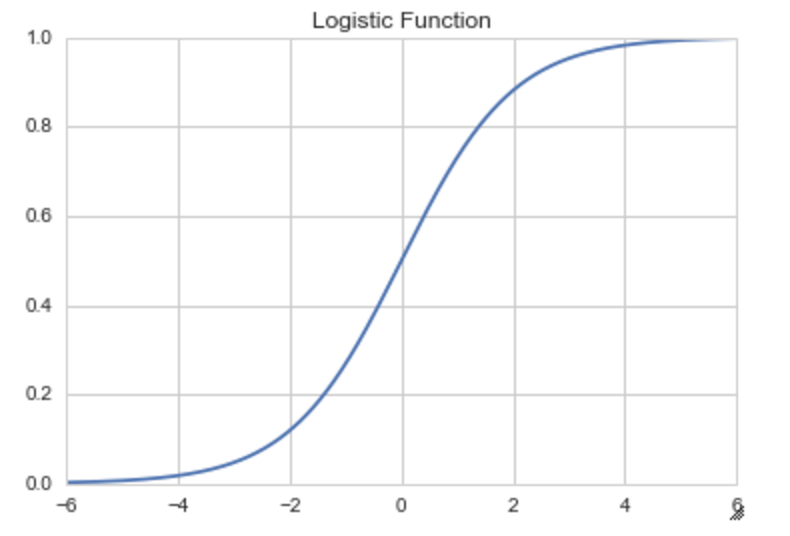
ロジスティック関数の形は以下となる。0〜1の値を取り、単調増加。
目的変数の行列xと説明変数yの関係は以下。(y=ax+bの右辺をexpの-1乗する形。)
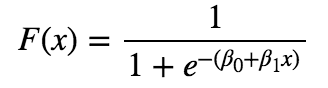
利用データ用意
sklearnで不倫用のデータを使う。
from sklearn.linear_model import LogisticRegression # ロジスティック回帰用
from sklearn.cross_validation import train_test_split # クロスバリデーションのsplit用
import statsmodels.api as sm
df = sm.datasets.fair.load_pandas().data # 不倫データのロード
不倫データの概要
df.head()

rate_marriage:幸せ度、age:年齢、yrs_married:結婚年数、children:子供の数、religious:信仰度、educ:最終学歴、occupation:妻の職業、occupation_husb:旦那の職業、affairs:不倫経験(0より大きいと不倫経験あり)、Had_Affair:不倫フラグ(affairsが0>なら1がセットされてる)
簡単に不倫有無と適当なサンプルの関係をみる
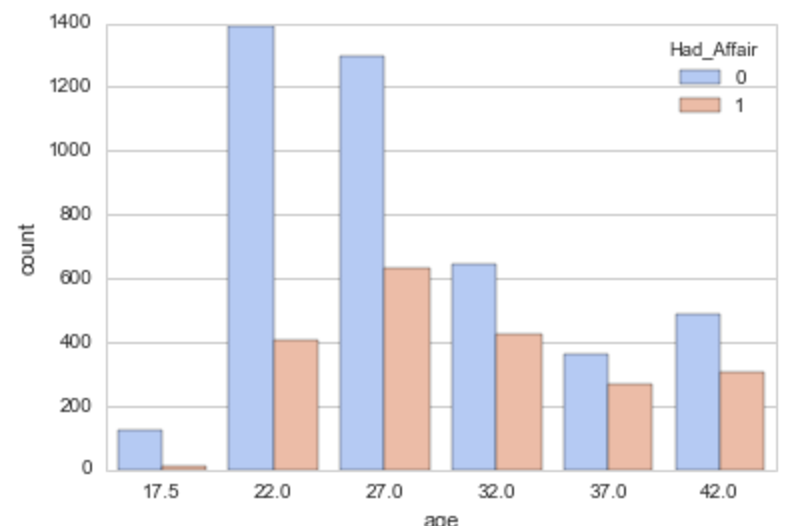
# 年齢と不倫有無
sns.countplot('age', data = df.sort('age'), hue = 'Had_Affair', palette='coolwarm')
# 結婚年数と不倫有無
sns.countplot('yrs_married', data = df.sort('yrs_married'), hue = 'Had_Affair', palette='coolwarm')

# 子供の人数と不倫有無
sns.countplot('children', data = df.sort('children'), hue = 'Had_Affair', palette='coolwarm')

年齢が上がる/結婚年数が多い/子供がいる方が不倫率が高い
※ ただし年齢が上がれば結婚年数が増えたり、子供の数が増えるなど、説明変数間でも関係性があると思われる。
ロジスティック回帰やってみる
前処理
やる前に、職業の変数がカテゴリ変数になっているので、これをダミー変数に置き換える。
カテゴリ変数とは、中の値の大小に意味がないもの。
# numpyのget_dummiesでdummy変数に変換。
occ_dummies = pd.get_dummies(df.occupation)
hus_occ_dummies = pd.get_dummies(df.occupation_husb)
# カラム名セット
occ_dummies.columns = ['occ1','occ2','occ3','occ4','occ5','occ6']
hus_occ_dummies.columns = ['hocc1','hocc2','hocc3','hocc4','hocc5','hocc6']
occ_dummies.head()

上の感じで、occ1〜6のうちどれに当たるかが0,1のフラグで置き換えてあげる。
続けて、説明変数を取得する。
# Xに、元のデータフレームから職業、旦那の職業、結婚有無を削除したものをセット。
X = df.drop(['occupation', 'occupation_husb', 'Had_Affair'], axis =1)
# 職業をダミー変数化したデータフレームを用意
dummys = pd.concat([occ_dummies, hus_occ_dummies], axis =1)
# 職業等を削除したデータフレームに、職業ダミー変数データフレームを結合
X = pd.concat([X, dummys], axis=1)
X.head()
多重共線性
ある説明変数が、他の説明変数を1つまたは複数で表現できる場合、多重共線性があるという。例えば今回は、occ1は、occ2〜occ6の値で一意に決まる関係にある。(occ2〜6に1が1個以上あれば、occ1=0、そうでなければocc1=1)
この場合、逆行列が計算できなかったり、計算できても得られる結果の信頼性が低くなってしまう。
なので、これをなくすべく、occ1とhocc1を削除する。
X = X.drop('hocc1', axis = 1)
X = X.drop('hocc1', axis = 1)
# affairsは、目的変数を作成するのに使っているので、これも説明変数から除く。
X = X.drop('affairs', axis =1 )
X.head()
最終的な形
sklearnを使って実行
# 目的変数セット
Y = df.Had_Affair
Y = np.ravel(Y) # np.ravelでYを1次元配列にする
# ロジスティック回帰実行
log_model = LogisticRegression() # インスタンス生成
log_model.fit(X, Y) # モデル作成実行
log_model.score(X, Y) # モデルの予測精度確認(72.6%)
> 0.7260446120012567
各変数の係数を確認
# インスタンスの.coef_[0]に、係数が入っている
coeff_df = DataFrame([X.columns, log_model.coef_[0]]).T
coeff_df

この係数が大きいところが、影響が多いところになる。
ただし、説明変数のデータの単位が統一されていないので、単純に横並びで比較はできない。
例えば、occ5はyrs_marriedの9倍くらいあるから、結婚年数は見なくてOK!!とは単純にならない。
ついでに
いつものごとく、trainとtestに分ける方法も書いとく。
# trainとtest用データ用意
X_train, X_test, Y_train, Y_test = train_test_split(X, Y)
log_model2 = LogisticRegression()
log_model2.fit(X_train, Y_train) # trainデータでモデル作成
class_predict = log_model2.predict(X_test) # testデータを予測
from sklearn import metrics # 予測精度確認用
metrics.accuracy_score(Y_test, class_predict) # 精度確認
>0.73115577889447236
73%くらいの精度が出てることがわかる。
