「機械学習と深層学習」の文献中に例題として取り上げられているプログラムを実装してみる。
文献ではC言語でプログラムを記述しており、これをPythonで自分なりに実装してみた。
今回は強化学習による迷路抜け知識の学習を取り上げる。
強化学習とは
- 一連の行動の最後に評価が与えられるような場合に用いる学習方法
例)将棋
-
教師あり学習の場合
コンピュータプレイヤーが一手ごとにその手の評価を先生から教わる方法- 効率的な学習は可能だが、大量の教師データを用意する必要があり大変
- 一手だけ取り出してその手が正しいかどうかは、多くの場合判断することができない
-
強化学習の場合
一連の着手が終了した後に評価を得て、その評価に基づいて学習を進める- ゲームの勝敗によって評価(勝ち、負け、引き分け) → 報酬
- 最終の評価から、一手一手の行動に関する知識を学習する
Q学習
- 強化学習を実現する方法として、Q学習がある
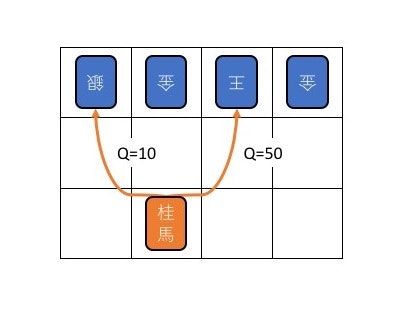
- ある場面において次にとるべき行動を選択するための指標 → Q値
- Q値に従って行動を選択する
例)将棋
- 次に選択できる手のそれぞれにQ値を与える
- Q値の大きさに従って次の行動をとる
- Q学習を繰り返していくとQ値の値が改善されていき、やがて選択が適切に行われるようになる
迷路抜け知識の学習
問題設定
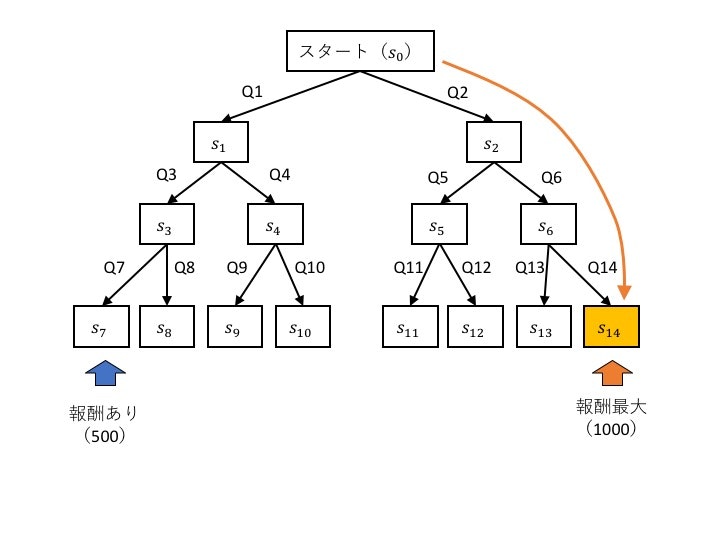
- スタート地点から開始
- 分岐を繰り返して最下段までたどり着くと、その場所に応じた報酬が得られる
- なるべく多くの報酬がもらえるような行動知識を学習する
- 今回はs14が最大の報酬を与え、s7が最大の半分の報酬を与えるとする
初期状態
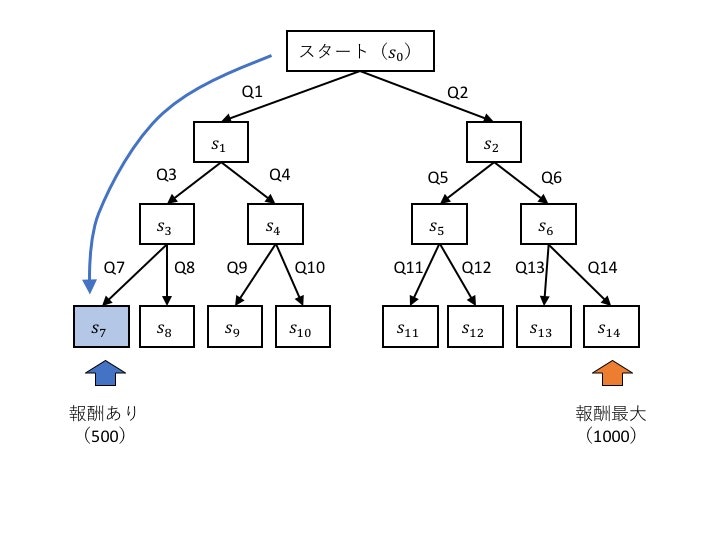
学習の初期の行動はランダムに選択される
初期状態でたまたま目標とする行動パターンに近いものが現れることがある
→ この時に得た報酬によってその行動パターンのQ値が増加
→ 次回からその行動パターンが選択されやすくなる
これでは…
報酬に直結する行動のQ値が改善されるだけで、初期の行動に対するQ値はランダムに決定された値のまま更新されない
そこで
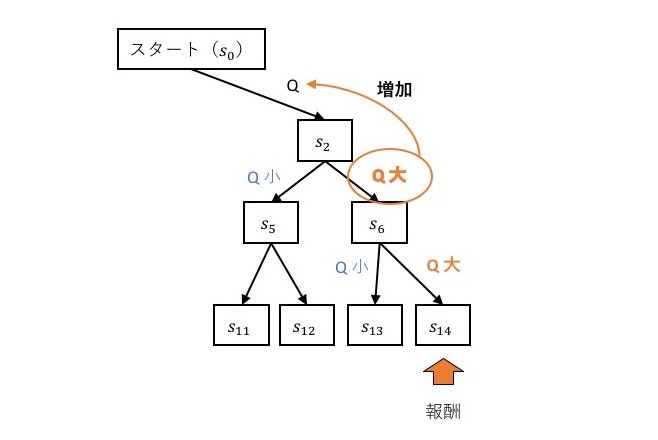
次の行動に移ったとき、選択可能な行動に対するQ値の中で、最大のQ値に比例する値を直前のQ値に加える
こうすることで
学習を繰り返していくと報酬を得ることができる行動パターンに対するQ値が増加する
Q値更新の計算
Q_{s_t,a_t} = Q_{s_t,a_t} + α(r + γ・max・Q{s_{t+1},a_{t+1}} - Q_{s_t,a_t})
- $s_t$: 時刻tにおける状態
- $a_t$:$s_t$において選択した行動を表す
- $max・Q_{s_{t+1},a_{t+1}}$: 次の時刻において選択できる行動に対するQ値の中で最大の値
- $r$: 報酬(得られなければ0)
- $α$: 学習係数(0.1程度)
- $γ$: 割引率(0.9程度)
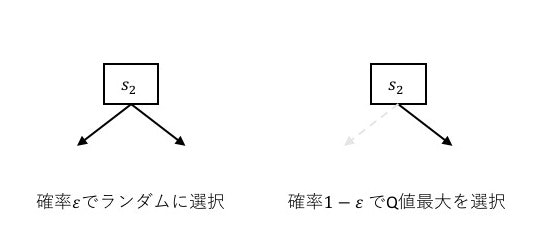
ε-グリーディ法
行動選択はQ値の大きい行動を優先する
→ 初期のランダムに決まったQ値がたまたま大きな値となった行動だけが常に選択されてしまう
そこで
- ある適当な定数を用意(ε = 0.3)
- 行動選択の際、0~1の間の乱数を生成し、その値がε以下であればランダムに行動を選択する
- εより大きければQ値の大きい行動を選択する
こうすることで
Q値の初期値に依存することなく、様々な行動に対する適切なQ値の学習が可能となる
Q学習の手順
- 全てのQ値をランダムに決定
- 学習が十分進むまで以下を繰り返す
- 動作の初期状態に戻る
- 選択可能な行動から、Q値に基づいて次の行動を決定する
- Q値を更新
- 報酬を得たら、報酬に比例した値をQ値に加える
- 次の状態で選択できる行動に対するQ値のうち、最大値に比例した値をQ値に加える
- 目標状態に至ったら2に戻る
- 2に戻る
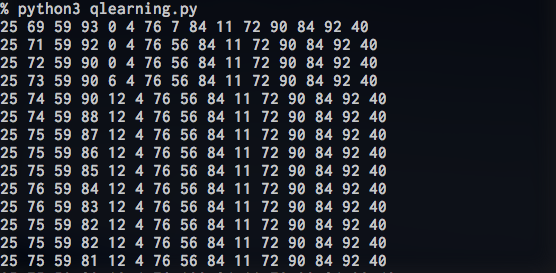
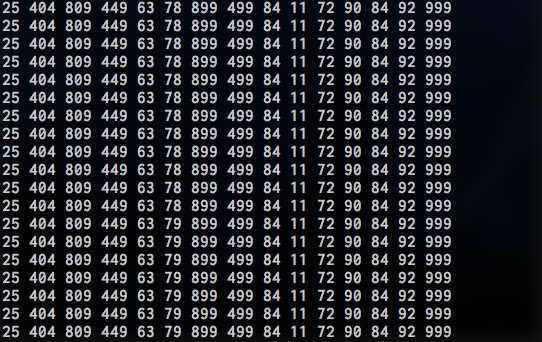
プログラム
プログラム => Github