More than 3 years have passed since last update.

週刊 JPEGデコーダをつくる #4 データ圧縮の基礎(中編)

Last updated at 2020-01-07Posted at 2017-04-21

データ圧縮の基礎(続き)

可逆圧縮の原理

JPEGコーデックは非可逆圧縮ですが、そのアルゴリズムには可逆圧縮を行う手続きが含まれています。実は あらゆる非可逆圧縮コーデックでは可逆圧縮アルゴリズムを利用する のです。まずは、全ての基本となる可逆圧縮の原理を理解しておきましょう。

説明用に単純化した、300×200ピクセル、3bpp、グレイスケール画像を考えます。3bppというのは耳慣れないかもしれませんが、その定義通り "1ピクセルを3ビットで表現" つまりピクセル値が 0～7 を取りうる8階調グレイスケール画像です。このデジタル画像を表現するには 300×200×3＝180000ビットが必要です。さて、このデジタル画像がもつ情報を全く損なわずに、もっと少ないビット量で表現することは可能でしょうか？

答えは：はい、可能です。デジタル画像がもつ データの統計的な偏りを利用すると、各ピクセル値はそのままに 情報を一切損なうこと無く、より少ないビット量で表現できる のです。これが可逆圧縮の原理です。この "より少ないビット量で表現" におけるビット量が、ピクセル値の集合というデジタル画像が持っている情報の量、つまり「エントロピー(entropy)」に対応します。¹

Let's ハフマン符号

騙されたように感じる方もいるでしょうから、具体的な数字で計算してみましょう²。先の3bppグレイスケール画像では、ピクセル値の度数分布データは下表の通りでした。表中 "ビット列" は各ピクセル値に対応する3ビット長のビットパターン、単に10進数ピクセル値から2進数へ変換したものです。

ピクセル値	度数(個数)	ビット列	ビット量小計
0	2	`000`	6
1	3744	`001`	11232
2	21245	`010`	63735
3	18457	`011`	55371
4	7284	`100`	21852
5	5661	`101`	16983
6	2967	`110`	8901
7	640	`111`	1920
合計	60000	-	180000

ではここで、魔法の（じゃないけど）対応表を取り出します。各ピクセルに対応するビット列が変化、つまりピクセル値0はビット列110000に、ピクセル値1はビット列1101にと対応させます。元々はビット長3で固定だったビット列が、新しい対応表ではビット長1～6の可変長となります。

ピクセル値	ビット列	ピクセル値	ビット列
0	`110000`	4	`1111`
1	`1101`	5	`1110`
2	`0`	6	`11001`
3	`10`	7	`110001`

この新しい対応表を使って、画像全体を表すのに必要となるビット量を求めます。ピクセル値0は6ビット必要で2個つまり6×2＝12ビット、ピクセル値1は4ビットが3744個つまり4×3744＝14976ビット、と計算していきます。最後に全ピクセル値0～7に対するビット量を合計すると 143602ビットです。³

ピクセル値	度数(個数)	ビット列	ビット量小計
0	2	`110000`	12
1	3744	`1101`	14976
2	21245	`0`	21245
3	18457	`10`	36914
4	7284	`1111`	29136
5	5661	`1110`	22644
6	2967	`11001`	14835
7	640	`110001`	3840
合計	60000		143602

変換前は画像全体で 180000ビットだったものが、ピクセル値とビット列の対応を変更した だけで 143602ビットへと縮みました。変換前後でのビット量比は 1:1.25 (1÷1.25=80%)、わずか20%ですがデータサイズ削減に成功しました。このとき、デジタル画像を構成するピクセル値は一切変化していませんから、この変換こそが可逆圧縮です！...納得できるまで読み返してくださいね。

ここで使った対応表は、JPEGコーデックでも利用する「[ハフマン符号(Huffman coding)][wp.huffmancoding]」によるものです⁴。ハフマン符号は[エントロピー符号(entropy coding)][wp.entropycoding]の一種であり、前節で説明したエントロピーつまり "データの統計的な偏り" を利用した可逆圧縮アルゴリズムです。⁵

偏ったデータ Is Awesome

データ圧縮は魔法ではなく数学ですから、どんなデータでも可逆圧縮できるとは限りません。エントロピー符号（ハフマン符号）による可逆圧縮の本質は "データの統計的な偏り" にあります。定性的な説明では：

データ値の分布が偏っているほどエントロピーは小さくなり、エントロピー符号化による大きなデータサイズ削減効果が見込めます。
データ値の分布に偏りがない、つまりデータ値が均等に出現するときにエントロピーは最大となり、エントロピー符号化ではデータサイズを全く削減できません。

可逆圧縮では、どんなデータに対してもサイズ削減できるアルゴリズムというものは原理的に存在しません。データ圧縮処理に逆変換が存在するには、全ての入力値に対して何らかの出力値を1:1対応させる必要があります。Nビットの入力データは全部で $2 ^ N$ 通り存在しますから、1:1対応させる圧縮後データもまた $2 ^ N$ 通り存在するはずです。$2 ^ N$ 通りのデータを一意に表現するには少なくともNビット必要ですから、とりうる入力データ全体で考えると入力ビット長＜圧縮後ビット長となる入出力値の組が必ず存在します。見方をかえると、可逆圧縮アルゴリズムでは入力ビット長＞圧縮後ビット長が成り立つ範囲（$2 ^ N$ 通りよりもずっと候補数の少ないデータ集合）だけを取り扱っているのです。

次に、わざとらしいグラデーション画像とランダム･ドット画像を考えます。いずれもピクセル値度数分布が均一な200x200ピクセル, 3bppグレイスケール画像ですから、前節と同じハフマン符号を適用してもそのデータサイズは全く削減されません。右のランダム・ドット画像はともかく、左のグラデーション画像もデータ圧縮できないというのには違和感がありませんか？

予測と変換

先ほどはピクセル値そのもにをエントロピー符号を適用しましたが、一般的な画像コーデックではピクセル値 x に対して何らかの事前計算 y = Fwd(x) を行い、その計算結果 y に対してエントロピー符号を適用します。一連のデータ処理過程で可逆圧縮を実現するには、計算 Fwd() が可逆(reversible)、つまり対応する逆計算 Inv() によりピクセル値が完全に復元 x == Inv(Fwd(x)) されなければなりません。このような計算として、画像・音声コーデックでは下記方式が利用されます：⁶

予測符号化(predictive coding)：ほかのデータ値から対象データ値を予測する。実際のデータ値と予測値から、その "ずれ量" を出力する。最も単純な予測アルゴリズムは、直近データ値を予測値とし(pred = x[n-1])、実データ値(x[n])との差分値(y = x[n] - pred)を出力する。この計算は[差分符号化(delta encoding)][wp.deltaencoding]と呼ばれ、JPEGコーデックでも利用される。
変換符号化(transform coding)：入力データ値の集まり(x[0:N])から、出力データ値の集まり(y[0:N])へとまとめて変換する。JPEGコーデックでは原画像を8x8ブロック分割し、各ブロックに含まれる64個のピクセル値ベクトル $\mathbf{x}$ に64x64要素の変換行列 $\mathbf{T}$ を掛け、64個の出力ベクトル $\mathbf{y}$ へと変換する($\mathbf{y} = \mathbf{T} \mathbf{x}$)。逆変換は変換行列 $\mathbf{T}$ の逆行列 $\mathbf{T}^{-1}$ により $\mathbf{x} = \mathbf{T}^{-1} \mathbf{y}$ となる($\mathbf{T}^{-1} \mathbf{T}= \mathbf{I}$)。JPEGコーデックでは $\mathbf{T}$ にDCT(discrete cosine transform)変換行列を用いる。

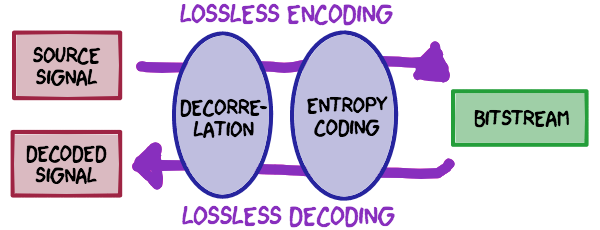
いずれもエントロピー符号化への入力データを "統計的に偏らせる" こと、元データが持っている[冗長性(じょうちょうせい)][wp.redundancy]を取り除く「[相関除去(decorrelation)][wp.decorrelation]」を目的としています。古典的なものから最新のものまで、ほとんどの実用的なデータ圧縮アルゴリズムは、相関除去とエントロピー符号化の組み合わせで構成されます。⁷

相関除去×エントロピー符号

先ほどのグラデーション画像とランダム・ドット画像に、差分符号化とハフマン符号を適用してみます。差分符号化エンコード／デコード処理は簡単なPythonコードで実装できます。x がデジタル画像のピクセル値、yがハフマン符号の対象となる差分値です。

差分符号化(Pythonコード)

# 差分エンコード処理: y[] = Fwd(x[])
def encode_delta(y, x):
  pred = 0
  for i in range(len(x)):
    y[i] = x[i] - pred
	pred = x[i]

# 差分デコード処理: x[] = Inv(y[])
def decode_delta(x, y):
  pred = 0
  for i in range(len(y)):
    x[i] = y[i] + pred
	pred = x[i]

この差分符号化とハフマン符号を組み合わせると、1ピクセルあたり平均ビット長は下表のようになります。グラデーション画像では原画像(3bpp)に対して平均ビット長 1.11bpp、ビット量比では 1:2.70 (＝3÷1.11)とそれなりにデータサイズ削減を達成しています。一方のランダム・ドット画像では原画像よりも増えて(+0.73bpp)しまいました。

画像	事前計算	エントロピー符号化	平均ビット長
グラデーション	（なし）	ハフマン符号	3.00 [bpp]
グラデーション	差分符号化	ハフマン符号	1.11 [bpp]
ランダム・ドット	（なし）	ハフマン符号	3.00 [bpp]
ランダム・ドット	差分符号化	ハフマン符号	3.73 [bpp]

差分符号化だけに着目すると、値のとりうる範囲がピクセル値(0～7の8段階)から差分値(-7～+7の15段階)へと広がるため、値表現に必要なビット数は一時的に3bitから4bitへと増えます。それでもグラデーション画像でデータサイズ削減ができたのは、差分値の度数分布が大きく偏っているためです。ピクセル値と差分値それぞれの度数分布表（ヒストグラム）を見比べると、"データの偏り" 度合いが大きくなったことが読み取れるかと思います。⁸

👈 [#3 データ圧縮の基礎(前編)][article3] ／ #5 データ圧縮の基礎(後編) 👉
[article3]: http://qiita.com/yohhoy/items/2740f4fa207a44f6bf4b

エントロピーは「平均情報量」、つまり "1ピクセルを表現するのに必要なビット量" という定義です。オリジナルのデジタル画像は 3bpp で表現されていましたが、本文中のデジタル画像に対してエントロピーを計算すると約 2.28bpp となります。画像全体では約 300×200×2.28＝136800ビットが必要です。エントロピーが小数値となるのは、それが平均値を表すためです。 ↩
ハフマン符号の構成とビット長計算、エントロピー計算に用いたコード：https://gist.github.com/yohhoy/0b98f913a553ee7a4b75cf97e56efe17 ↩
この説明には小さなごまかしがあります。変換後のビット列からピクセル値に戻すには、ピクセル値－ビット列の対応表それ自体をデータに含めなければなりません。JPEGビットストリームもこのような対応表データ（DHTセグメント）を含んでおり、そのデータサイズは数十バイト程度です。本文例示のように画像サイズが十分大きければ無視できる大きさです。
[wp.huffmancoding]: https://ja.wikipedia.org/wiki/%E3%83%8F%E3%83%95%E3%83%9E%E3%83%B3%E7%AC%A6%E5%8F%B7 ↩
ハフマン符号は、瞬時復号可能（＝デコード時にビット先読み不要）かつ一意復号化可能（＝入出力データが1:1で対応）なコンパクト符号（＝整数ビット長での最適な符号割り当て）として知られています。ハフマン符号はエントロピー符号アルゴリズムの中では（他と比較して）実装が簡単かつ動作も高速であり、データ圧縮の話題では無視できない[ソフトウェア特許問題][wp.softwarepatent]についてもクリアなため、多くのデータ圧縮アルゴリズムで採用されています。
[wp.softwarepatent]: https://ja.wikipedia.org/wiki/%E3%82%BD%E3%83%95%E3%83%88%E3%82%A6%E3%82%A7%E3%82%A2%E7%89%B9%E8%A8%B1
[wp.entropycoding]: https://ja.wikipedia.org/wiki/%E3%82%A8%E3%83%B3%E3%83%88%E3%83%AD%E3%83%94%E3%83%BC%E7%AC%A6%E5%8F%B7 ↩
理想的なエントロピー符号によるビット長（平均符号長）は、データのエントロピーに等しくなります。ハフマン符号はエントロピー符号化の一種ですが、例示画像では理論値 2.28bpp に対して少し悪い値 143602÷(300×200)＝2.39bpp となります。ハフマン符号では各ピクセル値に "整数個のビット" しか割り当てられないため、これは同アルゴリズムの性能限界なのです。JPEGコーデックもオプション的に対応する「[算術符号(arithmetic coding)][wp.arithmeticoding]」は、各ピクセル値に "実数個のビット" を割り当てることで、より短いビット長に変換することができます。より噛み砕いた（ただし正確でない）表現だと、複数ピクセル値の組に対してビットパターンを対応させます。また、算術符号では[ソフトウェア特許問題][wp.softwarepatent]も悩ましい話題であり、同アルゴリズム利用したソフトウェアを開発する場合には注意が必要です。
[wp.arithmeticoding]: https://ja.wikipedia.org/wiki/%E7%AE%97%E8%A1%93%E7%AC%A6%E5%8F%B7 ↩
既に "○○符号化" という単語がたくさん登場していますが、情報理論とくに符号理論の分野では、単に入力データから出力データへの写像（マッピング）を "符号化(coding)" と呼びます。また入力データが取りうる値を "アルファベット(alphabet)"、符号化処理により得られる出力データの値を "符号語(codeword)" と呼びます。
[wp.deltaencoding]: https://ja.wikipedia.org/wiki/%E5%B7%AE%E5%88%86%E7%AC%A6%E5%8F%B7%E5%8C%96
[wp.redundancy]: https://ja.wikipedia.org/wiki/%E5%86%97%E9%95%B7%E6%80%A7_(%E6%83%85%E5%A0%B1%E7%90%86%E8%AB%96)
[wp.decorrelation]: https://en.wikipedia.org/wiki/Decorrelation ↩
厳密な区分では、"エントロピー符号化" とはデータ圧縮の方法論が異なる "[辞書式圧縮(dictionary coder)][wp.dictionarycoder]" という可逆圧縮アルゴリズムのグループも存在します。GIFやPNG画像コーデックでは、辞書式圧縮に区分される[LZW(Lempel–Ziv–Welch)アルゴリズム][wp.lzw]を採用します。両アルゴリズムグループは排他的ということではなく、ZIPデータ圧縮の[Deflateアルゴリズム][wp.deflate]のように両者を組み合わせる可逆圧縮アルゴリズムも存在します。
[wp.dictionarycoder]: https://en.wikipedia.org/wiki/Dictionary_coder
[wp.lzw]: https://ja.wikipedia.org/wiki/Lempel%E2%80%93Ziv%E2%80%93Welch
[wp.deflate]: https://ja.wikipedia.org/wiki/Deflate ↩
グラデーション画像を[ImageMagick][imagemagick]でPNG圧縮すると、ファイルサイズ 638byte つまり (638×8)÷(200×200)＝0.13bpp まで縮みました。PNGコーデックも基本構造（予測符号化＋辞書式圧縮）は本文中アルゴリズムと同じですが、より[高度な予測符号化][png.predicator]を用います。ちなみにランダム・ドット画像では 3.10bpp となり、PNGコーデックでもデータサイズは削減されませんでした。
[imagemagick]: https://www.imagemagick.org/
[png.predicator]: http://www.libpng.org/pub/png/book/chapter09.html ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up