ようやく前回の続きで今回は後編です。
さてここでみなさんもう一度、原点に立ち返ってみましょう。なぜデータを集めて分析をするのか。それは利益を最大化したいからです。自分が得をするために、判断の根拠となる材料 (データ) を収集し、中身を整理して眺め、行動に結びつけて利益を得ます。
すなわちデータ分析には利益につながる明らかな動機 (目的) が存在し、また分析の結果を行動に結びつけて初めて価値が生まれます。
ゲームと投資
ここで投資の話をしてみましょう。
万人に正しい投資法というのは存在しませんが、たとえば株式においては市場で優位性を得るための前提条件がいくつかあります。
- 投資は確率のゲームである
- 市場はおおむね効率的である、しかしわずかな歪みが生じている
- 資本主義は自己増殖するので長期的には市場が拡大し、株価は経済成長率に収束する
これは古典的なアイテム課金型ソーシャルゲームにもある意味通じるものがあるのではないかと思います。すなわち 1. 確率のゲームであり 2. 歪み (偏り) があり 3. インフレが起こる、という点です。課金して目的のアイテムが得られるかどうかは確率である。すなわち同じ額「課金」したとしてもそれによって得られる「アイテム」と結果として結びつく強さには偏りがあります。また遅かれ早かれプレイヤー全員が強くなるのでインフレが起こり、強い新規アイテムが投入されれば過去のアイテムの価値は相対的に下がる。というところですね。もっともこれはシステムだとか、運営の方針などによって差があります。
どのみち、偶然の大当たりに依存せず確率を上げるためには戦略があります。それはたとえば試行回数を増やす戦略を取ることです。多少当たりが多かったり少なかったりしても、長く続けていけば平均的な値に収束するというものです。これは株式で言うと長期保有の戦略に似ています。株式にもひとつの銘柄を長期的に保有することで、一時的な高低はあっても評価額は結果的に上がるという話ですね。ウォーレン・バフェットが有名だと思います。もっとも、これは「良い株を長く持ちましょう」という話で、銘柄をよく吟味してその会社が「長期的に発展する」であろうことが大前提になると思います。吟味が大切なので、たとえば移り変わりの速い浮き沈みの激しい業界の銘柄を長期保有するのは悪手です。そうでなくても、この先行き不透明な時代において長期的に発展するであろうと自信の持てる企業といえばだいぶ限られてくるかとは思います。
試行回数を最大化するためにお金を節約する
さて、試行回数を増やす戦略を取るにしても、ガチャを回せば 1 回ごとにお金がかかりますし、どうしたら効率的に課金できるのかは工夫の余地があります。わかりやすいのは、ランキングなどでボーダー達成ギリギリ程度にさまざまなリソースの投入を抑えることで、必要最小限の投資に抑えるという方法ですね。やみくもに投資するのではなくボーダーの見極めが大切になるというわけです。
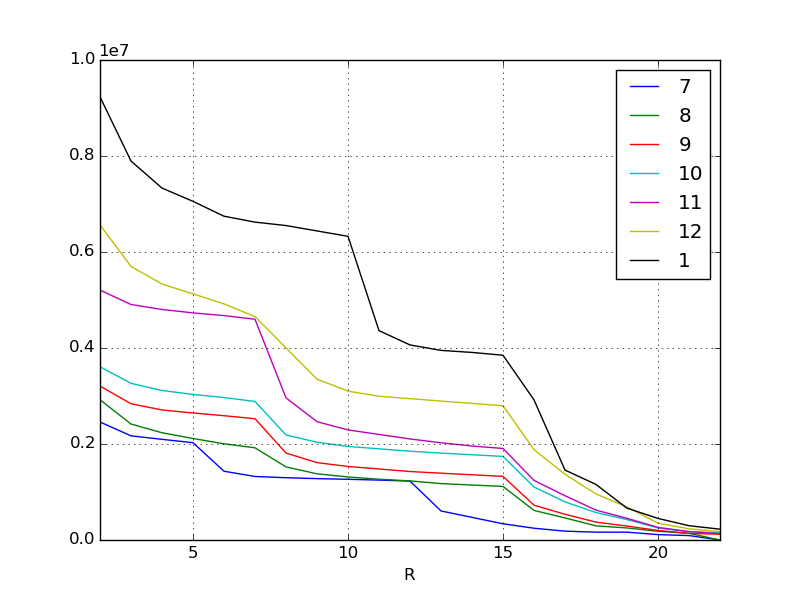
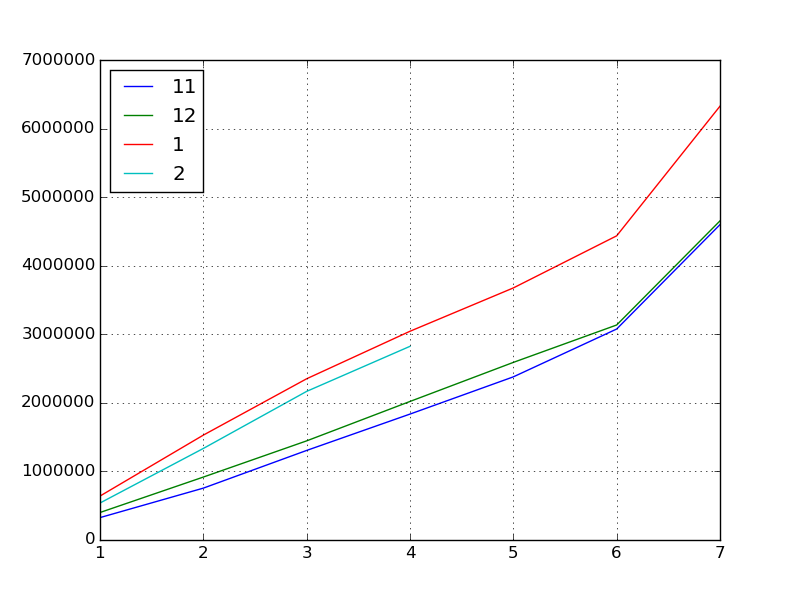
前回のグラフをあらためて思い出してみましょう。これは先月までの各月のイベントのスコアの伸びです。ここから傾向を割り出して 2 月のイベントのスコアを予測するのが目的です。
傾向をつかむ
可視化したデータを見てみるといくつかのポイントがあることがわかります。
たとえば 11 月は上位の報酬ランクのところに垂直に折れ曲がった崖ができています。また 1 月は下位報酬のところに崖ができていますね。これとイベントの内容を加味していくつかの仮説が立てられます。もちろんこの仮説は人間が考えなければなりません。もっともコンシューマ寄りの世界の出来事であれば、ソーシャルメディアや掲示板の情報を利用して人々の意見を拾い上げるという手もあります。
たとえば 11 月は
- 魅力的な新キャラクターが追加された (確実に入手するために上位報酬が人気に)
あるいは 1 月なら
- この直前に新システムが導入されてスコアの稼ぎ効率が向上した
- 冬に CM が放送されたのでそれにより新規課金勢が多数参入した
といった具合です。
いずれにせよ報酬の内容が変わる区切りに大きなスコアの差ができることが読み取れるわけですが、このように定性的な要因で顕著な変化があらわれてしまうのではうまく回帰式を導き出せません。
そこで今度はイベントが開始されてから、当月 (2 月) の日々のスコアを集計し、過去 3 カ月間と比較してどうだったかという観点で調べて行きます。
探索的データ解析
探索的データ解析とは「適切な目的や仮説を獲得する」という目的で、データを様々な角度からとらえ眺めてみることです。
本来、データ分析には明確な目的や仮説を必要とすることは再三に渡り強調してきましたが、そもそも分析対象に前提知識がなかったり、あるいは対象の実状をよくわかっていないという状況では、そもそもの目的や仮説を獲得するためにデータをいろいろと眺めてみる必要があるというわけです。これが統計学の世界で探索的データ解析と呼ばれるアプローチです。
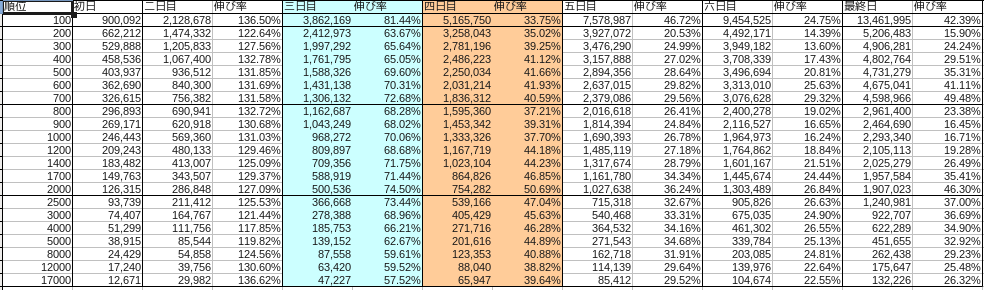
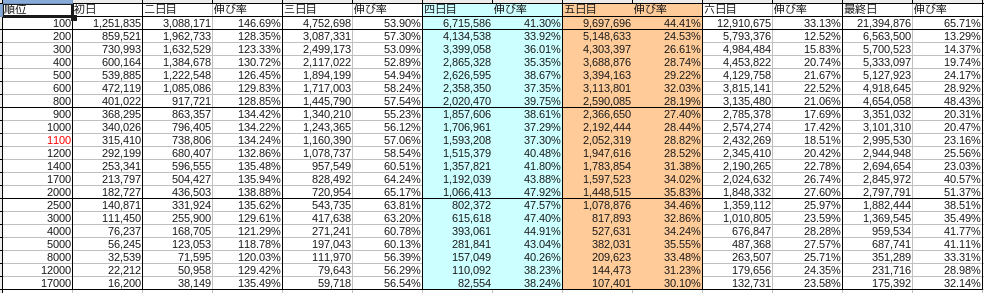
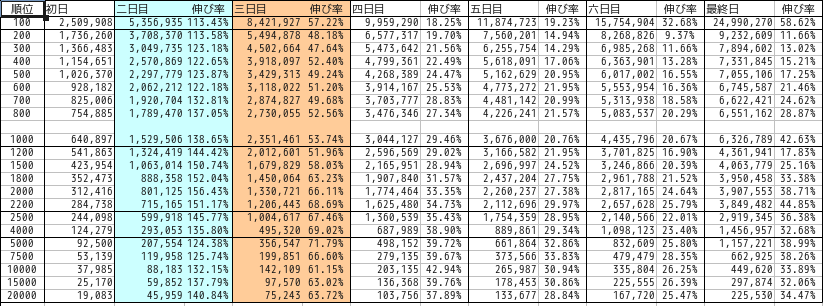
それぞれの月の内訳は以下の通りでした。
なお青は土曜、赤は日曜をあらわしています。
まずは狙いとして上位報酬にターゲットをしぼりましょう。各月の上位報酬にあたるボーダースコアの遷移をデータセットにしていきます。探索的データ解析を進めていくにはやはり IPython が便利です。
ここでは 2 月はイベントの中盤 (4 日目) まで経過したものとします。
# 各月の上位報酬のデータを切り出す
df201411 = pd.read_csv("201411.csv", index_col=0)
df201412 = pd.read_csv("201412.csv", index_col=0)
df201501 = pd.read_csv("201501.csv", index_col=0)
df201502 = pd.read_csv("201502.csv", index_col=0)
# 上位報酬の行をシリーズに抽出する
s201411 = df201411.ix[700, :]
s201412 = df201412.ix[800, :]
s201501 = df201501.ix[1000, :]
s201502 = df201502.ix[1000, :]
# 簡単のためインデックスを数字に
s201411.index = np.arange(1, len(s201411) + 1)
s201412.index = np.arange(1, len(s201412) + 1)
s201501.index = np.arange(1, len(s201501) + 1)
s201502.index = np.arange(1, len(s201502) + 1)
# 各月のシリーズを連結してデータフレーム化する
df = pd.concat([s201411, s201412, s201501, s201502], axis=1)
# カラムも数字にする
df.columns = [11, 12, 1, 2]
# 可視化する
df.plot()
つぎに基本統計量などを求めていきましょう。
# 基本統計量
df.describe()
# =>
# 11 12 1 2
# count 7.000000 7.000000 7.000000 4.000000
# mean 2040017.285714 2166375.142857 3143510.857143 1716607.750000
# std 1466361.613186 1444726.064645 1897020.173703 993678.007807
# min 326615.000000 401022.000000 640897.000000 539337.000000
# 25% 1031257.000000 1181755.500000 1940483.500000 1136160.000000
# 50% 1836312.000000 2020470.000000 3044127.000000 1751315.500000
# 75% 2727857.000000 2862782.500000 4055898.000000 2331763.250000
# max 4598966.000000 4654058.000000 6326789.000000 2824463.000000
# 相関係数
df.corr()
# =>
# 11 12 1 2
# 11 1.000000 0.999157 0.996224 0.996431
# 12 0.999157 1.000000 0.998266 0.997345
# 1 0.996224 0.998266 1.000000 0.999704
# 2 0.996431 0.997345 0.999704 1.000000
# 共分散
df.cov()
# =>
# 11 12 1 2
# 11 2.150216e+12 2.116705e+12 2.771215e+12 6.500842e+11
# 12 2.116705e+12 2.087233e+12 2.735923e+12 6.893663e+11
# 1 2.771215e+12 2.735923e+12 3.598686e+12 1.031584e+12
# 2 6.500842e+11 6.893663e+11 1.031584e+12 9.873960e+11
ここから何がわかるのでしょうか。
- 11 月、 12 月、 1 月と順調にスコアの「インフレ」が加速している
- とくに 1 月は顕著である (相関係数から読み取れる)
- 過去月もずっとインフレし続けているから、おそらく 2 月もインフレするのではないか
しかしながら、実際に 2 月のイベントが始まって 4 日が経ってみてフタを開けてみると……なんとスコアが下降してしまいました。
これは前回に出したデータを含めて今までにないことですね。ずっと上昇 (インフレ) してきたのに下降、初めての現象なのでいよいよ予想が難しくなりました。
ここでもまたいくつかの仮説を設定することになります。
- この月は特別なガチャなどいわゆる集金イベントが多かった
- 冬 CM 新規参入組が 1 月に十分戦力が整わないままイベントに参戦し無理な戦いを繰り広げて燃え尽きた
- 業界的に毎年 2 月には売上が下がる
- サービスインから 10 カ月が経過したため、報酬アイテムを 10 枚そろえた者が多くデッキの 10 枚を埋め終えたため競争が鈍化した
- 先月がインフレしすぎであったため、みなが節約しはじめた
いろいろ考えられます。
ただ、各月のどの伸びも相関係数が高いので、つまりは過去 3 ヵ月の日々の伸びを参考にイベント終了時点のスコアを予測しても良さそうだ、と判断できます。
スコアの伸びを騰落率でとらえる
そこでこのスコアの伸びを 騰落率 (percent change) でとらえます。
騰落率とはそもそも投資の用語で、価格の変動を示す指標のことです。 2 つの時点を比較してファンドの価値が何パーセント上下しているかを見ます。ここではスコアの伸びをファンドの価格変化のパターンととらえて騰落率を算出してみます。
# 前日からの伸び率
df.pct_change()
# =>
# 11 12 1 2
# 1 NaN NaN NaN NaN
# 2 1.315821 1.288455 1.386508 1.475449
# 3 0.726815 0.575413 0.537399 0.623495
# 4 0.405916 0.397485 0.294568 0.303079
# 5 0.295578 0.281922 0.207571 NaN
# 6 0.293197 0.210570 0.206691 NaN
# 7 0.494807 0.484321 0.426303 NaN
# 転置すると、前の月に対する伸び率になる
df.T.pct_change()
# =>
# 1 2 3 4 5 6 7
# 11 NaN NaN NaN NaN NaN NaN NaN
# 12 0.227813 0.213304 0.106925 0.100287 0.088689 0.019129 0.011979
# 1 0.598159 0.666635 0.626419 0.506643 0.419258 0.414710 0.359413
# 2 -0.158465 -0.127103 -0.078220 -0.072160 NaN NaN NaN
前日からの伸び率はどの月も同じ傾向にあります。休日か平日かによって伸び率に多少の差はあるものの 2 日目が一番伸びてその後ゆるやかになり、最終日のスパートで 40 〜 50 パーセント伸びるとわかります。
次に同じ日の前月からの伸びを見ると 2 月はマイナスに転じていますから
pct_change = df.T.pct_change() # 前月からの伸び率
def estimated_from_reference(day):
return df.ix[7, 1] * (1 + df.T.pct_change().ix[2, day])
estimated = [estimated_from_reference(x) for x in range(1, 7)]
print(estimated)
# =>
[5324211.8451061565, 5522634.3150592418, 5831908.3162212763, 5870248.3304103278, nan, nan]
# 1 日目、 2 日目、 3 日目、 4 日目を基準にした予想最終ボーダースコア
このように求まりました。
あるいはこれから来るであろう 5 日目、 6 日目、最終日のスコアをこう求めても良いでしょう。
def estimated_from_perchange(criteria, day):
return df.ix[criteria, 2] * (1 + df.pct_change().ix[day, 1])
# 2 月 5 日目のスコアを 1 月の 4 日目から 5 日目の騰落率より算出
df.ix[5, 2] = estimated_from_perchange(4, 5)
# => 3410740.086731
# 同じく 6 日め
df.ix[6, 2] = estimated_from_perchange(5, 6)
# => 4115709.258368
# 最終日
df.ix[7, 2] = estimated_from_perchange(6, 7)
# => 5870248.330410
これでデータフレームの欠損値が埋まりました。このことから 4 日目時点の予想としては 587 万点が上位報酬のボーダーではないかと予測できたわけです。
判断の材料にする
ちなみに正解データとして 5 日目 3487426 点 (4 日目予測値に対し 102.2%) 、 6 日目 4094411 点 (99.5%) 、 最終日 5728959 点 (97.5%) でしたので 587 万点なら余裕を持って上位報酬を獲得できたという結果になります。
| 日数 | 予測 | 結果 | 差異 |
|---|---|---|---|
| 5 日目 | 3410740 | 3487426 | 102.2% |
| 6 日目 | 4115709 | 4094411 | 99.5% |
| 最終日 | 5870248 | 5728959 | 97.5% |
探索的データ解析の結果は IPython の強力な機能でプログラムして残しておくことができますから、イベントの経過を追いつつ毎日計算すればきわめて高い精度でボーダーが予測できることが実証されました。
さいごに
投資の世界には騰落レシオという指標があります。これは全銘柄に対する騰落率の比率を見る短期的指標です。株が買われすぎであるかどうかといったことをこのテクニカル指標から読み取ることができます。
実績として 2015 年 3 月 4 日の日経平均を見てみましょう。
騰落レシオ 日経平均比較チャート
http://nikkei225jp.com/data/touraku.html
この日は売りが先行し午前中に日経平均が 200 円も下がりました。実はこの直前の騰落レシオを見ると 130 から 140 と非常に高い数値が見られます。これは要するに市場が強気で買われすぎということを指していて、このあと日経平均が急落するという予兆を示しています。実際に 200 円下がったあとは、レシオの数値が平常範囲内に戻り、買い戻しが発生して反発しています。
このように、ゲームのような小さな世界の数値分析も、金融経済の大きな世界の分析も、基本となる部分には共通のメソッドが適用できる部分があると言えるでしょう。もちろん突発的な大変化による不測の事態もあるでしょうが、日々物事を科学的に分析しようとする姿勢はとても大切です。