あるクラスの男子女子の 50 メートル走の記録から母分散を判定して仮説検定してみましょう。
ここでもう一度仮説検定と確率分布について考えてみましょう。
正規母集団 N(μ, σ^2) の母分散 σ^2 の検定を考えます。
あるサンプルを正規母集団 N(u, σ^2) からの標本とすると
T = \frac {nS^2} {\sigma^2} = \frac {1} {\sigma^2} {\sum_{k=1}^n} (X_k - \overline{X})^2 \\
は χ^2(n-1) に従います。
このときの χ^2(n-1) は自由度 n-1 の χ 二乗分布です。
このことから母分散 σ^2 の検定法が得られます。これがカイ二乗検定でした。
等分散仮説の検定
体育の授業で 50 メートル走の記録を計測しました。その結果は表に示すとおりでした。このクラスでは男子のほうが速いように見えますが、学年全体でも果たしてそうでしょうか。
| 性別 | 人数 | 平均タイム | 標準偏差 |
|---|---|---|---|
| 男子 | 7 | 7.9 | 0.9 |
| 女子 | 8 | 9.0 | 0.7 |
確かに男子のほうが速そうです。このとき、男子女子のタイム全体を正規分布に従うと仮定します。ふたつの N(μ, σ^2) のグループができるわけですが、それぞれの σ^2 が等しいかどうかわかりません。したがいまして等平均仮説の検定がおこなえません。そこではじめに分散を検定します。
男子女子それぞれを N(μ_a, σ^2_a), N(μ_b, σ^2_b)とし、不偏分散 U^2_a, U^2_b とすると
T = \frac {U^2_a/\sigma^2_a} {U^2_b/\sigma^2_b}
は自由度 (N_a-1, N_b-1) の F 分布に従います。
F 分布
F 分布は自由度を持ちますが、 F 分布の自由度は自然数 (m,n) というペアで、自由度 (m,n) の F 分布を F(m,n) と表記します。
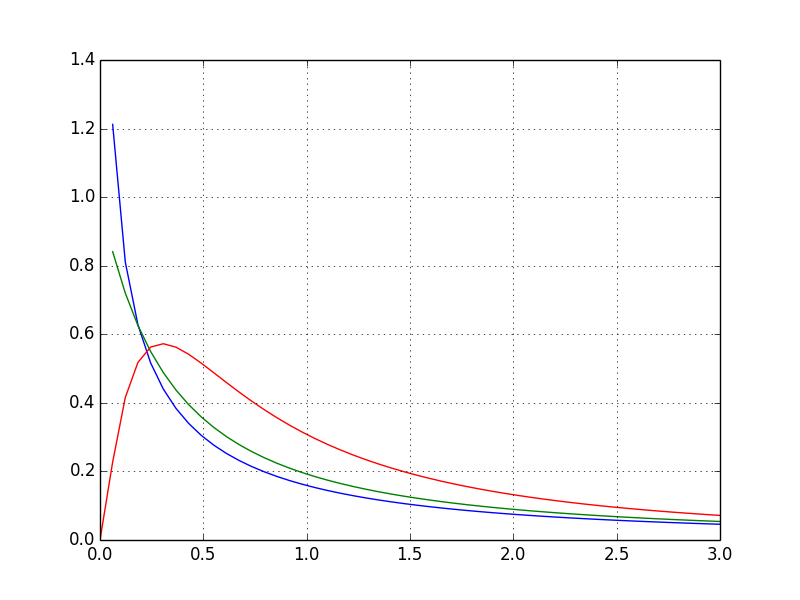
さっそく F(m,n) の密度関数を SciPy で生成し、プロットしてみましょう。
import numpy as np
from scipy.stats import f
import matplotlib.pyplot as plt
def draw_graph(dfn, dfd):
rv = f(dfn, dfd)
x = np.linspace(0, np.minimum(rv.dist.b, 3))
plt.plot(x, rv.pdf(x)) # 描画する
draw_graph(1, 1) # F(1,1) を青で
draw_graph(2, 1) # F(2,1) を緑で
draw_graph(5, 2) # F(5,2) を赤で
plt.grid(True)
plt.show()
plt.savefig('image.png')
一般的に X, Y が独立でありそれぞれ χ^2(m) および χ^2(n) に従うとき、 T = (X/m)/(Y/n) が従う分布を自由度 (m,n) の F 分布と言います。
先ほどの例で有意水準を 0.05 とすると Na - 1 = 6, Nb - 1 = 7 で自由度 (6,7) の 2.5% は F 分布の数表から
F_7^6 (0.025) = 5.12 \\
F_7^6 (0.975) = \frac 1 {F_6^7 (0.025)} = 1/5.70 = 0.18
となります。
U_a^2 , U_b^2, T の実現値は
\mu_a^2 = \frac {7 × 0.9^2} {7-1} = 0.945 \\
\mu_b^2 = \frac {8 × 0.7^2} {8-1} = 0.560 \\
t = \frac {\mu_a^2} {\mu_b^2} = \frac {0.945} {0.560} = 1.69 < 5.12 = F_7^6(0.025)
となりますので、帰無仮説 σ_a^2 = σ_b^2 は棄却されません。
そこであらためて等平均仮説の検定をおこないます。
N(\mu_a, σ^2_a) : n_a = 7, \overline{X}_a = 7.9, S_a = 0.9 \\
N(\mu_b, σ^2_b) : n_b = 8, \overline{X}_b = 9.0, S_b = 0.7
したがって
t = \frac {\overline{X}_a - \overline{X}_b} {\sqrt{ (\frac 1 {N_a} + \frac 1 {N_b}) × \frac {{N_aS_a^2} + {N_bS_b^2}} {(N_a - 1) + (N_b - 1)}} } \\
= \frac {7.9 - 9.0} {\sqrt{ (\frac 1 7 + \frac 1 8) × \frac {{7 × 0.9^2} + {8 × 0.7^2}} {(7 - 1) + (8 - 1)}} } \\
= -2.47
これは棄却域に属するので U_a = U_b は棄却されます。したがいまして 50 メートル走は男子のほうが速いことになります。
参考
ゼロから学ぶ統計解析
http://www.amazon.co.jp/dp/4061546562/