金融・経済分野への応用
pandas は 2008 年頃から金融の現場で開発され始めたデータツールです。作者の Wes McKinney は金融分野の有名なクオンツヘッジファンド AQR Capital Management に在籍していました。そのためか金融・経済データの実践的な分析ツールとして見ても強力な機能をいくつも備えています。
Yahoo! ファイナンスから取得したデータセットを pandas を使って分析していきます。今回使うのはいくつかの株式銘柄データと S&P 500 インデックス (銘柄の識別子が SPX のもの) の日毎の終値によるデータです。
データセットの読み書き
pandas には CSV や JSON などを始めとした入出力のための関数があります。
| 関数 | 説明 |
|---|---|
| read_csv | ',' 区切りのデータを読み込む |
| read_table | タブ ('\t') 区切りのデータを読み込む |
| read_json | JSON 形式のデータを読み込む |
| read_msgpack | msgpack 形式のデータを読み込む |
| read_pickle | バイナリデータを読み込む |
データフレームにはこれらと対になる to_XXX 関数が用意されており任意の形式でデータを出力できます。いちいち CSV や JSON の Parser を呼んでコードを書かなくていいのはとてもラクですね。
import pandas as pd
stock = pd.read_csv('stock_px.csv', parse_dates=True, index_col=0)
しかも CSV などから読み込んだデータには自動的にインデックスが作成されます。新しいオブジェクトをより適した新しいインデックスで再作成することもできます。
また pandas の特徴として欠損値の扱いが充実していることも挙げられます。データ分析において欠損の無いクリーンなデータをいつも取り扱えるとは限りません。そこで pandas のオブジェクトの統計値はすべて欠損値を除外します。欠損値をどの程度許容するか閾値を設定したり、指定した値で穴埋めをすることもできます。
データセットの取り扱い
要約統計量を求めたり集約、インデックスレベルによるグルーピングはいとも簡単にできます。
stock.head(10) # 先頭の 10 件のみ表示
# =>
# AAPL MSFT XOM SPX
# 2003-01-02 7.40 21.11 29.22 909.03
# 2003-01-03 7.45 21.14 29.24 908.59
# 2003-01-06 7.45 21.52 29.96 929.01
# 2003-01-07 7.43 21.93 28.95 922.93
# 2003-01-08 7.28 21.31 28.83 909.93
# 2003-01-09 7.34 21.93 29.44 927.57
# 2003-01-10 7.36 21.97 29.03 927.57
# 2003-01-13 7.32 22.16 28.91 926.26
# 2003-01-14 7.30 22.39 29.17 931.66
# 2003-01-15 7.22 22.11 28.77 918.22
stock['AAPL'].sum() # 合計
# => 277892.75
stock['AAPL'].mean() # 算術平均
# => 125.51614724480578
stock['AAPL'].median() # 中央値
# => 91.45500000000001
加重平均の算出
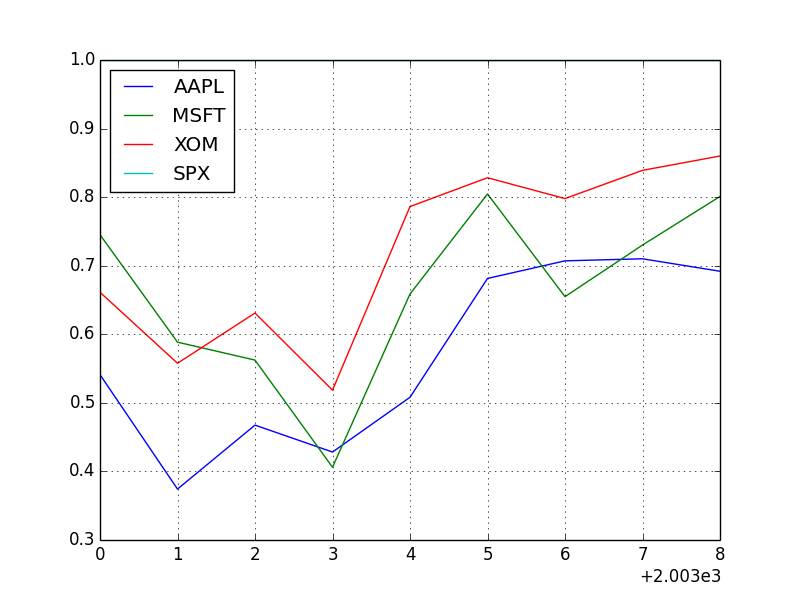
年次において日次の利益と SPX でどれくらい相関があるか求めてみましょう。
rets = stock.pct_change().dropna()
spx_corr = lambda x: x.corrwith(x['SPX'])
stock_by_year = rets.groupby(lambda x: x.year)
result_1 = stock_by_year.apply(spx_corr) # 日次の利益と SPX との相関
print( result_1 )
# => AAPL MSFT XOM SPX
# 2003 0.541124 0.745174 0.661265 1
# 2004 0.374283 0.588531 0.557742 1
# 2005 0.467540 0.562374 0.631010 1
# 2006 0.428267 0.406126 0.518514 1
# 2007 0.508118 0.658770 0.786264 1
# 2008 0.681434 0.804626 0.828303 1
# 2009 0.707103 0.654902 0.797921 1
# 2010 0.710105 0.730118 0.839057 1
# 2011 0.691931 0.800996 0.859975 1
plt.figure() # キャンバスの描画
result_1.plot() # matplotlib でプロットする
plt.show()
plt.savefig("image.png")
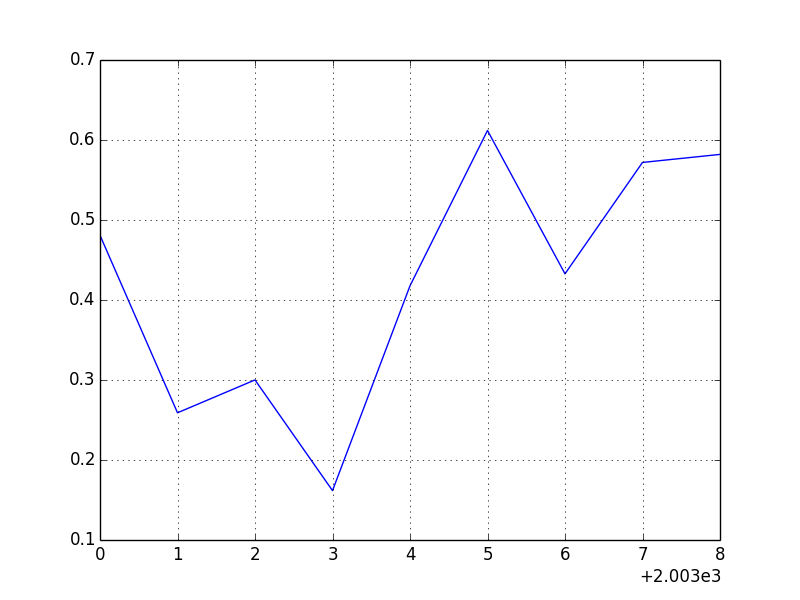
列どうしの相関を求めます。
result_2 = stock_by_year.apply(lambda g: g['AAPL'].corr(g['MSFT'])) # アップルとマイクロソフトの相関
print( result_2 )
# =>
# 2003 0.480868
# 2004 0.259024
# 2005 0.300093
# 2006 0.161735
# 2007 0.417738
# 2008 0.611901
# 2009 0.432738
# 2010 0.571946
# 2011 0.581987
plt.figure()
result_2.plot()
plt.show()
plt.savefig("image2.png")
線形回帰
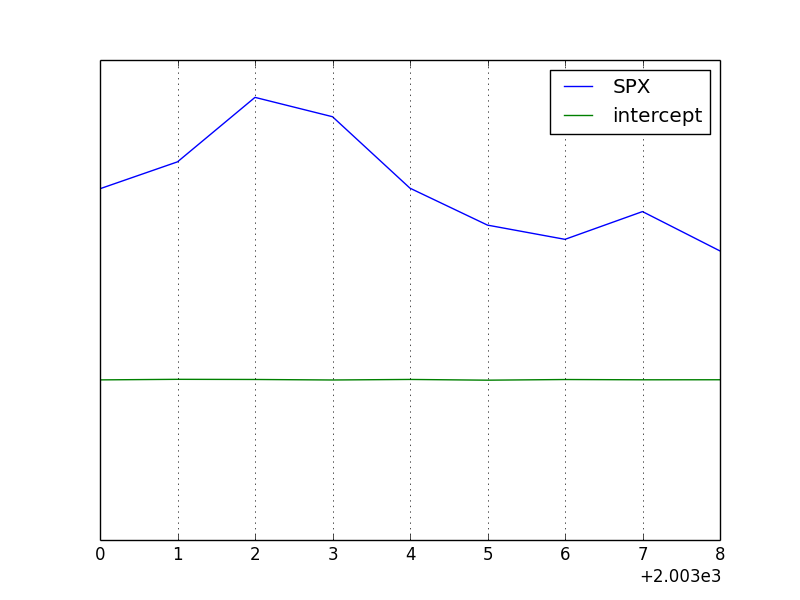
最小二乗法によるデータの線形回帰を求めます。
def regression(data, yvar, xvars):
Y = data[yvar]
X = data[xvars]
X['intercept'] = 1.
result = sm.OLS(Y, X).fit()
return result.params
result_3 = stock_by_year.apply(regression, 'AAPL', ['SPX'])
print(result_3)
# => SPX intercept
# 2003 1.195406 0.000710
# 2004 1.363463 0.004201
# 2005 1.766415 0.003246
# 2006 1.645496 0.000080
# 2007 1.198761 0.003438
# 2008 0.968016 -0.001110
# 2009 0.879103 0.002954
# 2010 1.052608 0.001261
# 2011 0.806605 0.001514
plt.figure()
result_3.plot()
plt.show()
plt.savefig("image3.png")
参考
Pythonによるデータ分析入門――NumPy、pandasを使ったデータ処理
http://www.oreilly.co.jp/books/9784873116556/