モンティ・ホール問題を解く

モンティ・ホール問題

みなさんは有名なモンティ・ホール問題をご存知でしょうか。

詳細な解説は上のリンク先に譲るとして、問題の概要はこうです。

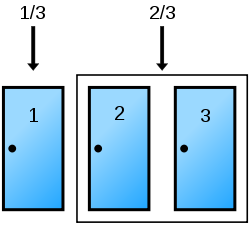
• 閉じられたドアが 3 つあります

• 3 つのドア A,B,C のうち 1 つには景品 (自動車) が入っています。

• 残りの 2 つはハズレ (ヤギ) が入っています

• あなたは 1 つのドアを選びます

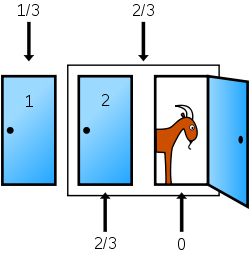
• あなたが選んでいないドアのうち、ハズレのドアを司会者が開けます

• さて、あなたはドアを選びなおしてもいいし、選びなおさなくてもいい

さて、このとき、ドアを選びなおしたほうが自動車が当選する確率が上がるでしょうか。それとも選びなおさなくても確率は一緒でしょうか？

最初は 3 つのドアのどれに自動車が入っているかわからない。

選んでいないドアのうち、ハズレがオープンになる。

この状態で、ドアを選びなおしてもいいし、選びなおさなくてもいい。

(画像はウィキペディアより転載)

みなさんも、ひとまず考えてみてください。

物議を醸した問題

ギネスブックで世界でも最も IQ が高いとされるマリリン・ボス・サバントは 1990 年、選びなおしたほうが選びなおさないより自動車が当たる確率は 2 倍になると回答し、物議を呼びました。

これに対し、読者から「彼女の解答は間違っている」との投書が 1 万通殺到し、そのうち 1000 名は博士号保持者であり「ドアを変えても確率は五分五分 (1/2) であるから倍の 2/3 にはならない」というものでした。

生涯に 1500 もの論文を発表した数学者であるポール・エルデシュは「ありえない」と、他にもジョージ・メイソン大学のロバート・サッチス博士は「プロの数学者として、一般大衆の数学的知識の低さに憂慮する。自らの間違いを認める事で現状が改善されます」と、フロリダ大学のスコット・スミス博士「君は明らかなヘマをした（中略）世界最高の知能指数保有者自らが数学的無知をこれ以上世間に広める愚行を直ちに止め、恥を知るように！」と、他にも著名な博士が次々と批判し物議を醸します。

さて正解は一体どうなのでしょう。

問題をシミュレーションする

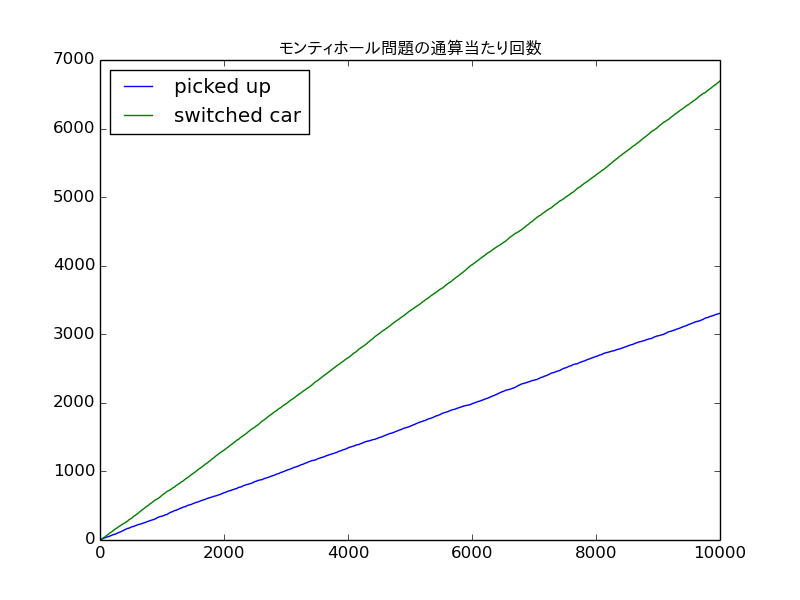
この問題はコンピューターでモンテカルロ法によるシミュレーションをおこなうことで、サバントの回答が正しかったことが実証されます。つまり、はずれのドアが明らかになったのち再度ドアを選び直すと、確率は 2 倍になるのです。

さっそく Python でシミュレーションしてみましょう。

import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import font_manager
from random import choice

def montyhall(N, doors):
    """ モンティ・ホール問題を解いて勝利したかどうかのベクトルを返す """
    # 試行回数と同じ長さのベクトルを用意する
    arr_picked = np.zeros(N)
    arr_switch = np.zeros(N)

    for i in range(N):
        car = choice(doors) # 車が入っているドアをランダムに決める
        picked = choice(doors) # 正解だと思うドアを選ぶ

        # 司会者がヤギの入ったドアをオープンする
        goat = choice(list(set(doors) - set([picked, car])))

        # 選びなおす
        switch = choice(list(set(doors) - set([picked, goat])))

        # それぞれのベクトルの該当の位置に正解かどうかの結果を格納する
        if picked == car:
            arr_picked[i] = 1 # 選びなおさなかった場合に正解なら 1
        if switch == car:
            arr_switch[i] = 1 # 選びなおした場合に正解なら 1

    # 2 つのベクトルを返却する
    return (arr_picked, arr_switch)

def plot(N, arr_picked, arr_switch):
    """ 結果をプロットする """
    # フォントを環境にあわせて指定しておくと便利
    if sys.platform == "darwin":
        font_path = "/Library/Fonts/Osaka.ttf"
    else:
        font_path = "/usr/share/fonts/truetype/fonts-japanese-gothic.ttf"
    prop = font_manager.FontProperties(fname=font_path)

    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)

    X = np.arange(N) + 1 # 試行回数を X 軸に持ってくる
    picked_car = arr_picked.cumsum() # 累積正解数を求める
    switch_car = arr_switch.cumsum()

    ax.plot(X, picked_car, label='picked up')
    ax.plot(X, switch_car, label='switched car')
    ax.set_title('モンティホール問題の通算当たり回数', fontproperties=prop)
    ax.legend(loc='best')
    plt.savefig('image.png')

def main(args):
    N = 10000 # 10000 回シミュレーションする
    doors = np.array([1, 2, 3])

    # モンティホール問題を解く
    (arr_picked, arr_switch) = montyhall(N, doors)
    # 結果をプロットする
    plot(N, arr_picked, arr_switch)

    # 累計勝利数を算出する
    win_picked = arr_picked.sum()
    win_switch = arr_switch.sum()

    print("ドアを変更しなかった場合: %f %% (%d)" %
          (100.0 * win_picked / N, win_picked))
    print("ドアを変更した場合:      %f %% (%d)" %
          (100.0 * win_switch / N, win_switch))

#=> 10000 回のゲーム中
#   ドアを変更しなかった場合: 33.060000 % (3306)
#   ドアを変更した場合:      66.940000 % (6694)

↑ switched car (選びなおした場合) は正解率が明らかに 2 倍となっています。

まとめ

この問題は、ベイズ統計学の基礎となる事後確率の説明によく使われます。すなわち、最初にドアが 3 つあってどれかに自動車が入っている確率が「事前確率」、司会者がドアをオープンしてヤギが見えたあとの確率が「事後確率」となるわけです。ベイズ統計についてはまた別の機会で説明をしましょう。

20 年前の著名な数学者がまちがえたような問題でも、今日では手元の計算機を利用して自由なソフトウェアのみで簡単に実証実験ができるわけです。極端な話、わたしたちはわずか 20 年前の数学者をも凌駕するデータ分析能力を獲得したとも言えます。もちろんこれは誇張ではありますが、このように手を動かして計算機を動かしデータを実際に分析することで物事の真実を明らかにすることができることは確かです。現実の問題に直面した場合でも計算機で科学的に検証する能力を身につけましょう。