この週で学ぶこと
- 異常検知
- レコメンダーシステム
#異常検知とは
異常検出問題とは、データが問題あり・なさそうなのを決定する
得られたデータで確率モデルを作り、テストデータの確率が閾値より小さければ
それは異常と判断する。
Ng先生「異常検知自体は教師なし学習でありながら、ある側面では教師あり学習の性質も持つ。」
応用例）
- エンジンの品質保障テスト（QA）：エンジンの振動、音などを特徴とする。
- 詐欺検出不審なユーザの検出：ユーザの行動（訪問時間やタイピングスピードなど）を特徴とする。
- データセンターコンピュータの負荷or故障監視：マシンのメモリ、ディスクアクセススピード、CPUロード時間などを特徴とする。
#異常検知のアルゴリズム
- 特徴を選択する
- 各トレーニングデータをモデルを適用し、パラメータを決定する
- 新しいデータ$x$に対し、データの発生確率$p(x)$を計算する。もし閾値より小さいならばそれは異常と判定する。
例）多数のサーバーの中から異常な振る舞いをしているサーバーを検出したい場合
1 特徴選択
特徴を各サーバーのスループット(mb/s), 応答遅延(ms)の2次元ベクトルとする。
2 各トレーニングデータiに対し、モデルを適用しパラメータを決定する
ラベル無しのトレーニングデータセット$\{x^{(1)},...,x^{(m)}\}$ （ここで$x^{(i)} \in\unicode{x211D}^2$）をプロットしてみる（下図）。
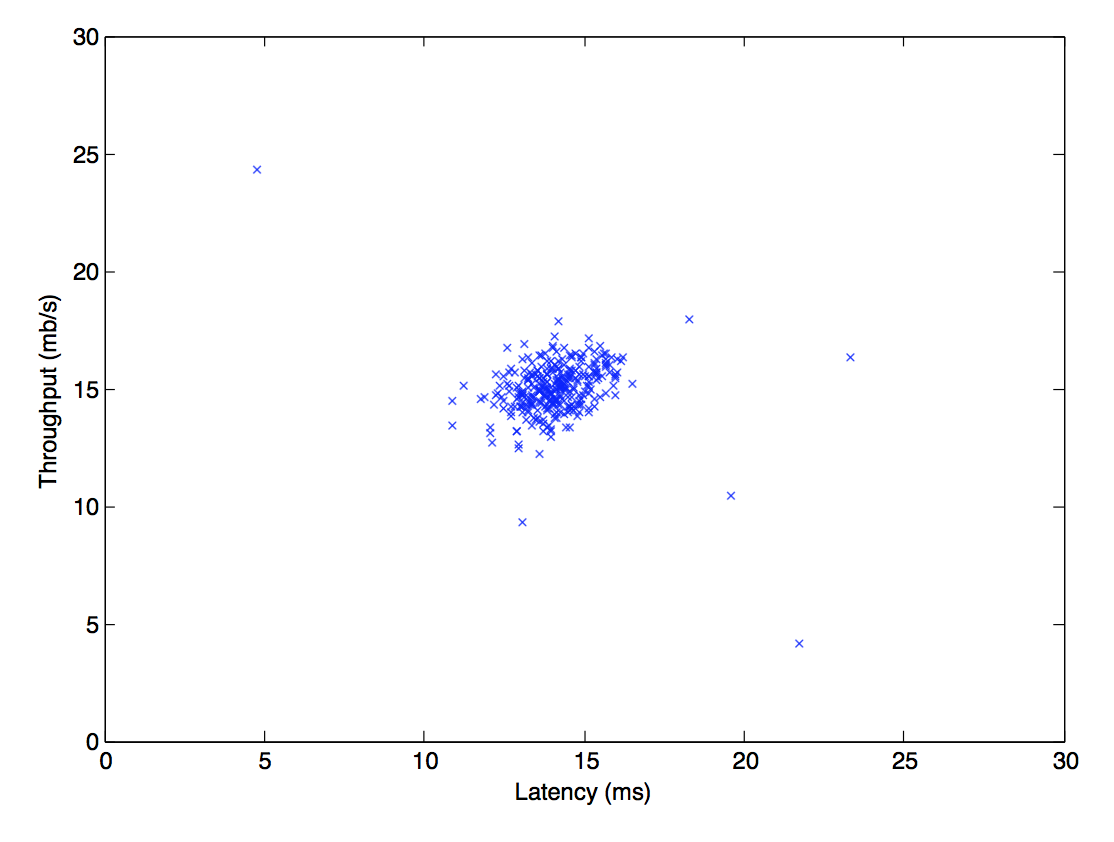(参考：宿題の図より)
各特徴$x_{i}$に対し次式のようにガウス分布を当てはめることを考える。
p(x_{i};\mu_{i},\sigma_{i}^2)=\frac{1}{\sqrt{2\pi \sigma_{i}^2}}\exp{\left\{-\frac{(x_{i}-\mu_{i})^2}{2\sigma_{i}^2}\right\}}
各特徴$i=1...n$（この例では$n=2$）に対して、$i$次元目の特徴 $\{x_i^{(1)},...,x_i^{(m)}\}$から$\mu_{i}$, $\sigma^{2}_{i}$を求める。
つまりこの例の場合はスループットと遅延の平均、分散を次式で求める。
\mu_{i} = \frac{1}{m}\sum_{j=1}^{m}(x^{(j)}_{i}),
\sigma_{i}^{2} = \frac{1}{m}\sum_{j=1}^{m}(x^{(j)}_{i}-\mu_{i})^2
すると、下図のように、用いたデータセットに対してガウス分布をフィッティングできる。
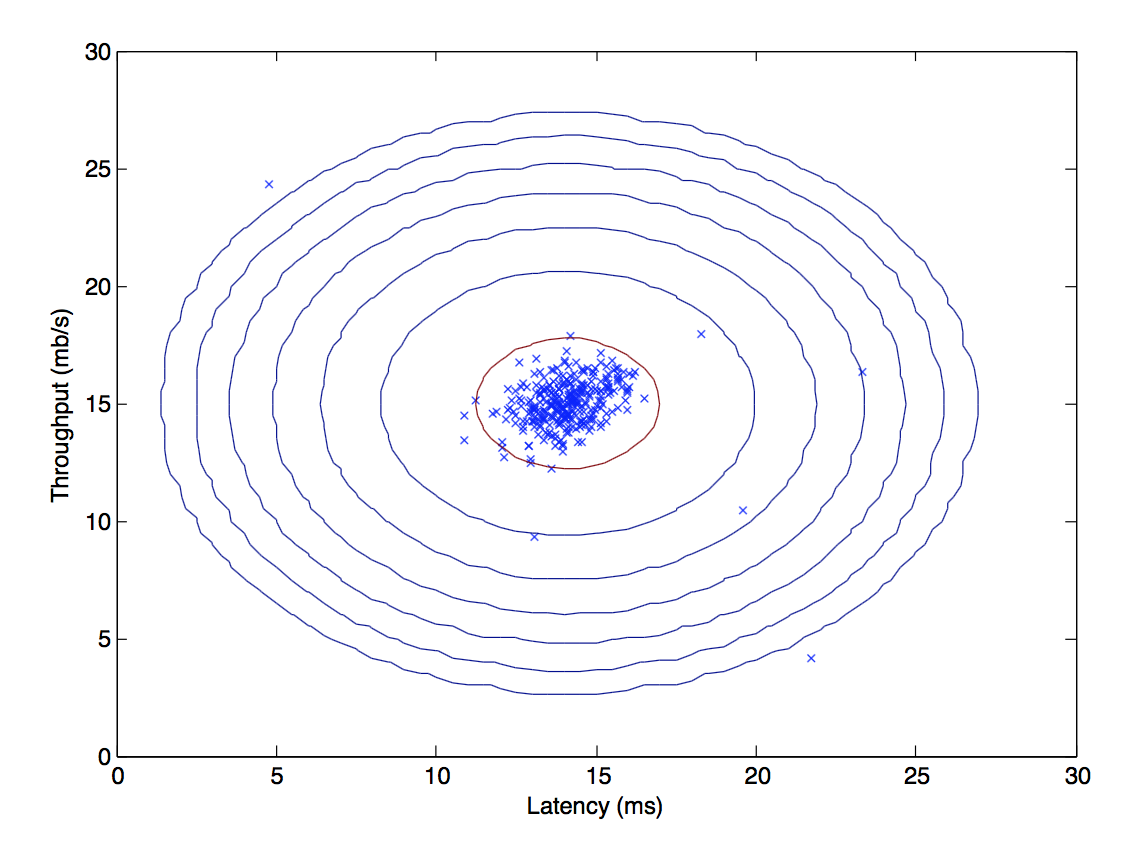
3． 新しいデータ$x$に対し、$p(x)$を計算する
p(x) = \prod_{j=1}^{n} p(x_{i};\mu_{i},\sigma_{i}^2) = \prod_{j=1}^{n}\frac{1}{\sqrt{2\pi \sigma_{i}^2}}\exp{\left\{-\frac{(x_{i}-\mu_{i})^2}{2\sigma_{i}^2}\right\}}
$p(x) < \epsilon$ならば異常と判定する。下図の赤で示した点が異常データ。$ε$の求め方は後述。
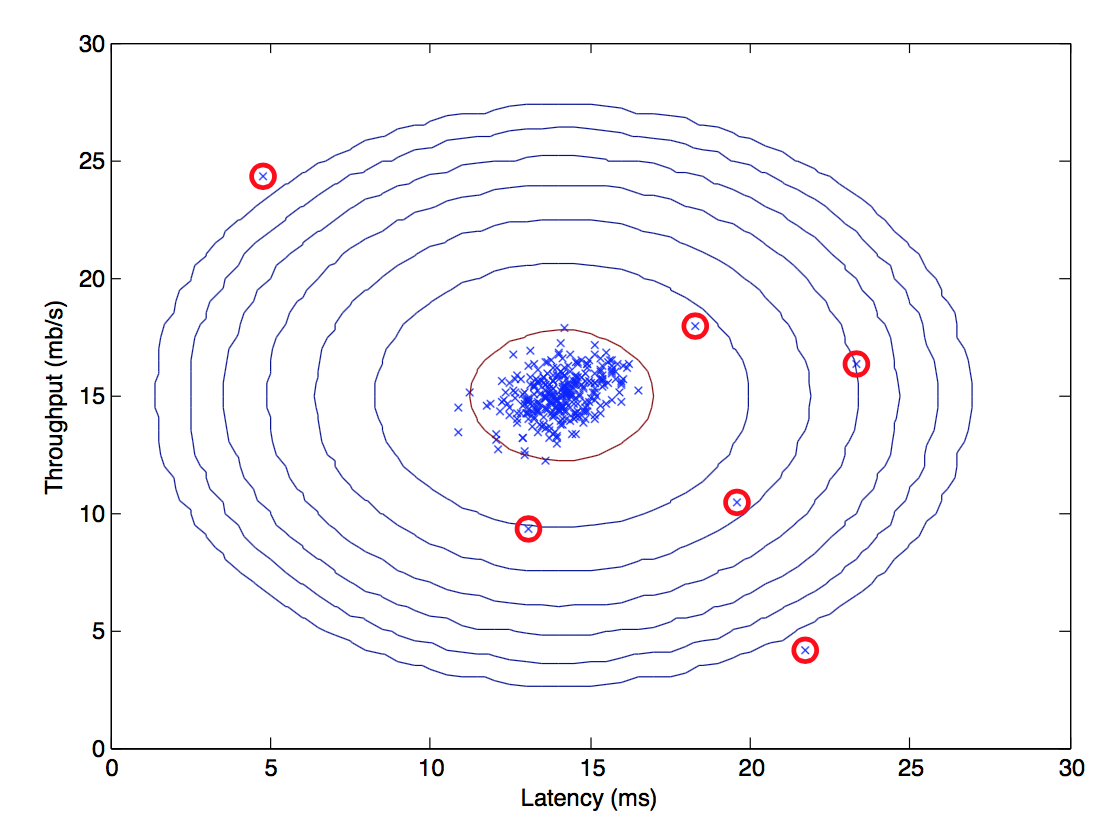
#異常検出アルゴリズムの評価
なぜ評価が必要なのか？
異常検知アルゴリズムを開発途中で、新しい特徴を加えることがよくある。これによりパフォーマンスが向上したかどうかを教えてくれる指標が必要だから。また、$ε$を適切に選ぶするときにも使う。
トレーニングセット、クロスバリデーションセット、テストセットの分割
異常検知の評価のためには、実際には、あるラベル付けされたデータを仮定する。
このデータは、過去のデータを使ってラベル付けすることができる。
例）飛行機エンジンの異常検出
正常データ数10000、異常データ数20の（ラベルづけされた）データがあるとする。
そのとき、下表のようにして各データセットに割り振る。
| データセット | 正常データ数 | 異常データ数 | 役割 |
|---|---|---|---|
| トレーニングセット | 6000 | 0 | P(x)をフィットするのに使う |
| クロスバリデーションセット | 2000 | 10 | F１スコアが最大になるεを決定するのに使う |
| テストセット | 2000 | 10 | 最終的なモデルの評価を行うのに使う |
異常データに関しては、CV,テストデータだけに分割する。**トレーニングセットに正常データしか含まれていないのは、正常データでモデルを作り、モデルから外れたデータを異常と見なしたいから。**ちなみに、10000のなかに少し異常データが紛れ込んでいてもOK。
F1スコアは、次式で求められる。
F_{1} = \frac{2 *prec*rec}{prec + rec}
Precision（適合率、精度）とRecall（再現率）は、次式で求められる。
prec = \frac{tp}{tp + fp}
rec = \frac{tp}{tp + fn}
ただし、
$tp$: 正解 → 異常、予測 → 異常 の数
$fp$: 正解 → 正常、予測 → 異常 の数
$fn$: 正解 → 異常、予測 → 正解 の数
##異常検出と、教師あり学習の使い所の違い
異常検知のトレーニングデータにラベルがついているなら、教師あり学習でいいじゃないか、ということになる。異常検知と教師あり学習は使いどころが異なる。
- 異常検出
陽性データ数：0～20
陰性データ数：多数
用いられるフィールド：欠陥検出、製造、モニタリング（多くの欠陥、多くの不良品があるなら教師ありになりうる）
陽性（異常）データの特徴を少数のデータから学習するのは難しいため、多数あるデータから学習しそれに外れたデータを検出するほうが現実的。貴重な陽性データは、CV,テストデータのために取っておく。
- 教師あり学習
陽性データ数：多数
陰性データ数：多数
用いられるフィールド：スパム検出、天気予報、ガン判定
陽性（異常）トレーニングデータも多数あるため、特徴自体の予測がしやすい。
##特徴の選定方法
異常検出のパフォーマンスに大きな影響を与えるのが、特徴の選定。
- 前処理：データをガウス分布へ変換する
プロットしてみて、ガウス分布でない場合は、様々な変換式をかましてガウス分布にする。 - 方法１：誤差解析
モデルを学習し、CVにかけて誤差をみる。特徴を追加したあとに誤差がどうなるかみるというのが誤差解析。特徴の作り方は、CVで間違って判定したものを取ってきて、そこから分析して新しい特徴を作る方法がある。 - 方法２：特徴同士の組み合わせから新しい特徴を作る
x1 = CPU負荷、x2=ネットワークトラフィックの場合、x3 = CPU負荷／ネットワークトラフィック とするなど既存の特徴の組み合わせから新しい特徴を作成する。
#レコメンダーシステム
##レコメンダーシステムとは
２種のアプローチを講義では学習する。
- コンテンツベースのレコメンデーション
- 協調フィルタリング
このうち、協調フィルタリングはアルゴリズム自体が何の特徴を使うかを学習する「フィーチャーラーニング」というおもしろい性質をもつ。
##コンテンツベースのリコメンデーション
コンテンツの内容に関するベクトル（映画の例だと各映画がもつ特徴$x_1$ :ロマンス, $x_2$:アクションなど）が既に与えられていると仮定した場合に、それを用いてレコメンデーションを行う手法。
###例）映画のレーティングを予想する
下表のようなレーティング（評価）データがあるとする。各値は0~5をとるとする。
| 映画 | Alice | Bob | Corol | Dave | $x_1$（ロマンス） | $x_2$（アクション） |
|---|---|---|---|---|---|---|
| Love at last | 5 | 5 | 0 | 0 | 0.9 | 0 |
| Romance forever | 5 | ? | ? | 0 | 1.0 | 0.01 |
| Cute puppies of love | ? | 4 | 0 | ? | 0.99 | 0 |
| Nonstop car chases | 0 | 0 | 5 | 4 | 0.1 | 1.0 |
| Swords vs. karate | 0 | 0 | 5 | ? | 0 | 0.9 |
右２列は、それぞれの映画がもつ各特徴（ジャンル）を数値化したものである。
問：ここから、どうやって?部分を予測するか？
方法：各ユーザの?を予測するために「各ユーザ毎に」パラメータΘを決める。そして、各ユーザ$j$に対し、パラメータ$\theta^{(j)}\in\unicode{x211D}^{n+1} $を学習する。各映画$i$に対し、ユーザ$j$は$(\theta^{(j)})^Tx^{(i)}$の評価をつける。
例）AliceがCute puppies of loveをどう評価するか予測したい場合
$x^{(3)}=(1,0.99,0)^T$ で、どうにかして$\theta^{(1)}=(0,5,0)^T$が得られたとすると、
(\theta^{(1)})^T * x^{(3)} = 5*0.99 = 4.95
と予測できる。つまり、ユーザの評価を、映画の特徴ベクトルとユーザのパラメータベクトルの内積で求める。では、どうやってこの$\theta^{(j)}$を求められるだろうか。
###目的関数の定義と最小化
予測値と正解値から線形回帰の問題と同じ考えで求めることができる。
\min_{\theta^{(j)}}\frac{1}{2}\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum_{k=1}^{n}(\theta_{k}^{(j)})^2
================================================
ユーザiが映画jを評価したなら$r(i,j)=1$、そうでないなら０
$y^{(i,j)}$ 正解データ
$\theta^{(j)}$ ユーザjのパラメータメータベクトル
$x^{(i)}$ 映画iの特徴ベクトル
$m^{(j)}$ ユーザjが映画を評価した数
これをすべてのユーザのパラメータ$\theta^{(1)}, \theta^{(2)},...,\theta^{(n_u)}$で求めるために、下式のようになる。
\min_{\theta^{(1)},...,\theta^{(n_u)}}\frac{1}{2}\sum_{j=1}^{n_u}\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_{k}^{(j)})^2
各項の前に$\sum_{j=1}^{n_u}$が前に追加されただけである。
###最急降下法によるパラメータ推定
最急降下法による$\theta_k^{(j)}$の更新ルールは下記の通り。
\theta_k^{(j)}:=\theta_k^{(j)} - \alpha \sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})x_k^{(i)} (k = 0のとき)
\theta_k^{(j)}:=\theta_k^{(j)} - \alpha\Biggl(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})x_k^{(i)} + \lambda\theta_k^{(j)}\Biggr) (k \neq 0のとき)
上記式の$\alpha$から右側は、
\frac{\partial}{\partial \Theta^{(j)}_{k}}J(\Theta^{(1)},...,\Theta^{(n_u)})
と等価である。見てわかるとおり、線形回帰で出てきた式とほとんど同じである。
##協調フィルタリング
多くのユーザの嗜好情報を蓄積し、あるユーザと嗜好の類似した他のユーザの情報を用いて自動的に推論を行う方法論。
コンテンツベースのように特徴$x$の各値を人手で決めるのは、とても困難。なので$x$の値は自動的に決定する（フィーチャーラーニング）。
このためには、コンテンツベースの手法とは逆に、各ユーザの$\theta$が分かっているという仮定をおく。そして、学習データと照らし合わせながら、リーズナブルな$x$をきめてゆく。
##例）映画のレーティング
以下のようなデータがあるとする。
| 映画 | Alice | Bob | Corol | $x_1$（ロマンス） |
|---|---|---|---|---|
| Love at last | 0 | 1.5 | 2.5 | ? |
一番右の列の$x_1$を求めたい。
このとき、$\theta^{(1)}=(0,0)^T$, $\theta^{(2)}=(0,3)^T$, $\theta^{(3)}=(0,5)^T$はすでにわかっているものとする。
(\theta^{(1)})^T x^{(1)} \approx 0
(\theta^{(2)})^T x^{(1)} \approx 1.5
(\theta^{(3)})^T x^{(1)} \approx 2.5
の条件を満たす$x^{(1)}$をもとめればよい。求めると、
x = (1, 0.5)^T
となる。
###目的関数の定義と最小化
これも、線形回帰のときに行ったものとほとんど同じとなる。コンテンツベースのときとは逆で、$\theta^{(1)},...,\theta^{n_u}$が与えられたときに、**特徴$x^{(i)}$**を次式で求める。
\min_{x^{(i)}}\frac{1}{2}\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum_{k=1}^{n}(\theta_{k}^{(i)})^2
これを**すべての映画の特徴$x^{(1)}, x^{(2)},...,x^{(n_m)}$**に渡って求めるために、上式は下式のようになる。
\min_{x^{(1)},...,x^{(n_m)}}\frac{1}{2}\sum_{i=1}^{n_m}\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_{k}^{(i)})^2
###コンテンツベースの手法と強調フィルタリングの手法の式のまとめと、新しい目的関数の定義
コンテンツベースの手法と強調フィルタリングの手法の式をまとめると、
- $x$が与えられたときに$\theta$を求める問題
- $\theta$が与えられたときに$x$を求める問題
となる。これは鶏と卵の問題であるが、両方を求めるためには、$\theta$ → $x$ → $\theta$ → $x$ → ...と、交互に二つを更新してゆけばよい。そのとき、初期値にはランダムな値を使う。
しかし、さらにこれを同時に推定することで計算コストを下げる方法がある。それは、目的関数に二つの手法の目的関数を突っ込んで次式のように１つの目的関数にしてしまう手法である。
J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}) = \frac{\lambda}{2}\sum_{(i,j):r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})^2 + \frac{\lambda}{2}\sum_{i=1}^{n_m}\sum_{k=1}^{n}(x_{k}^{(i)})^2 + \frac{\lambda}{2}\sum_{j=1}^{n_u}\sum_{k=1}^{n}(\theta_{k}^{(j)})^2
この式は、単純に２つの式を１つにまとめたものになっている。
そして、これを最小化するような$x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}$を同時に推定する。
「最小化」とはつまり、次式のことである。
min_{x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}} J(x^{(1)},...,x^{(n_m)}, \theta^{(1)},...,\theta^{(n_u)})
###まとめ：協調フィルタリングアルゴリズム
1.$x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}$を小さな値でランダムに初期化する
2.学習： $J(x^{(1)},...,x^{(n_m)}, \theta^{(1)},...,\theta^{(n_u)})$を最急降下法の以下の更新式により最小化する
x_k^{(i)}:=x_k^{(i)} - \alpha\Biggl(\sum_{j:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})x_k^{(i)} + \lambda x^{(i)}_{k}\Biggr)
\theta_k^{(j)}:=\theta_k^{(j)} - \alpha\Biggl(\sum_{i:r(i,j)=1}((\theta^{(j)})^Tx^{(i)} - y^{(i,j)})x_k^{(i)} + \lambda \theta^{(j)}_{k}\Biggr)
3.予測： あるユーザのパラメータ$\theta$とある映画の特徴$x$から、そのユーザのその映画への評価を予測する