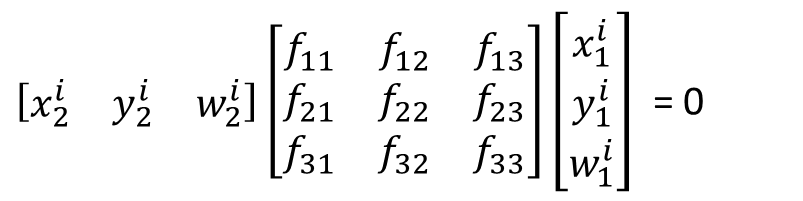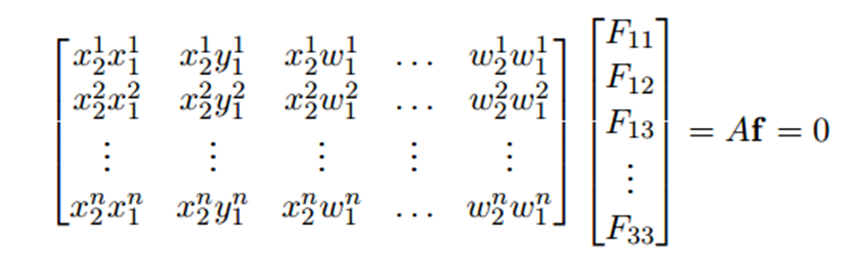はじめに
ネコ、かわいいですね〜
この記事では、コンピュータビジョン分野で取り扱われる、多視点画像から3次元世界を復元する技術について、ネコと一緒に学んでいく記事です。
この分野は現在でも研究が進められている分野で難しい数式も出てきて時には辛くなりますが、その辛さがネコと一緒に学ぶことで中和されれば幸いです。
この記事は「実践コンピュータビジョン」の、第5章「5.1 エピポーラ幾何、5.2 カメラと3D構造を使った計算」に相当します。
多視点画像から3次元世界を復元したい
冒頭のネコの画像は2次元画像でした。では、このネコの3次元形状を復元するにはどうしたらよいでしょうか?
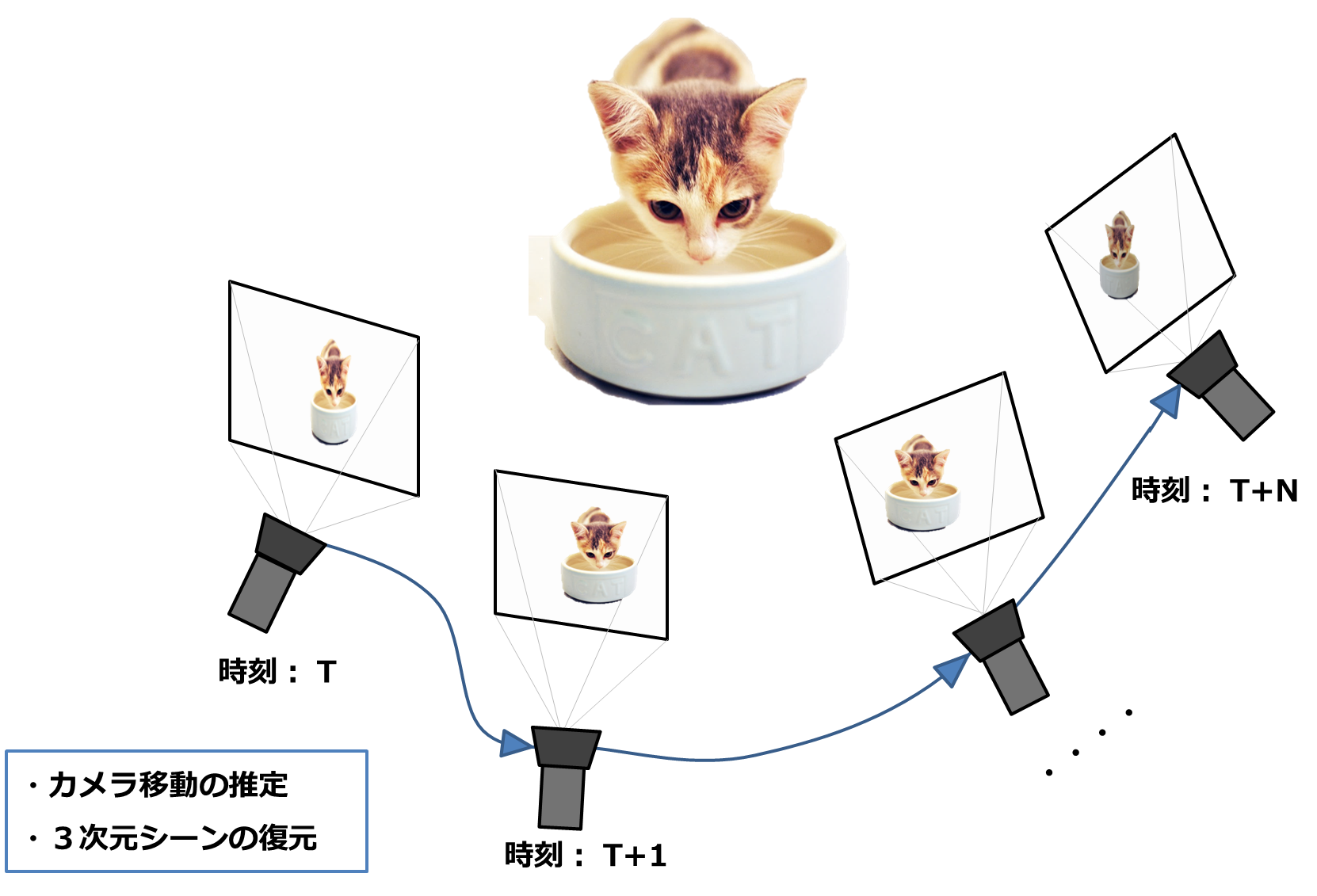
正解は、カメラをネコに向けて移動しながら、複数の視点から撮影するです。
それぞれの視点でネコがどのように映るかをてがかりに、カメラの姿勢の変化と、そのカメラが撮影しているネコの幾何学な構造を逆計算します。
これは、Structure from Motion(SfM)と呼ばれています。
手順は以下の通りです。
-
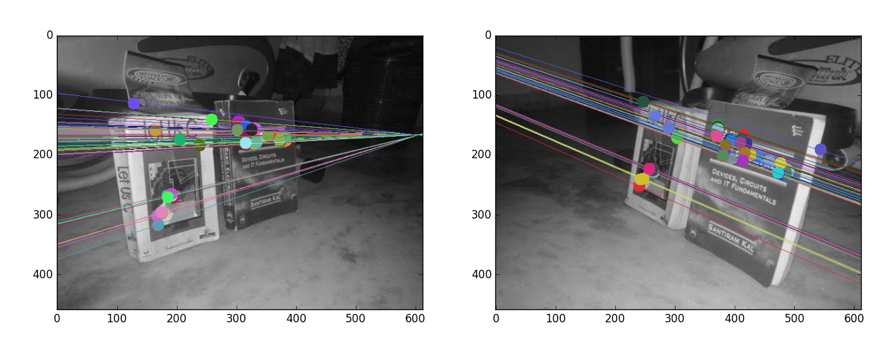
1. 対応点をみつける
対応点というのは、例えばネコの手を別々の視点から見ているときにそれぞれの画像に映る点のペアのことです。視点の移動前後の画像の対応点を見つけることで、どのように移動したかという手がかりになります。 -
2. カメラの運動を推定する
対応点を手がかりに、視点がどのように移動したのかを推定します。 -
3. 3Dシーンを再構築する
対応点とカメラの移動推定結果を手がかりに、3次元形状を復元します。 -
4. 全体の最適化
カメラ移動の度に2.や3.を繰り返すことによって、カメラ移動・3Dシーン復元誤差が蓄積します。これを解消するために、全ての対応点や視点運動の推定結果を使って、実測値と推定値との誤差が最小となる最適解を求めることで、全体の精度を向上させます。
ここでは問題を簡単にするために、画像のペアを考えます。つまり2視点のみを考えます。
この画像間に生じる基本的な理論をまず解説します。その後、カメラ運動の推定や3Dシーンの再構築を行っていきます。4.の全体の最適化は視点が多い場合のみ必要な処理なので、ここでは考えないことにします。
エピポーラ幾何 is 何?
2視点の画像からカメラの運動や3Dシーンの復元を行う前に、エピポーラ幾何という基礎的な理論をおさえる必要があります。
エピポーラー幾何とは、2つのカメラで同じ3次元物体を異なる視点から撮影したときに生じる幾何のことです。
エピポーラー幾何を体系立てている要素が、次に紹介するエピポーラ平面、エピポーラ線、エピポール、基礎行列,そして基本行列です。
エピポーラ幾何で出てくる超重要な5つのワード
-
エピポーラ平面 (図の青い平面)
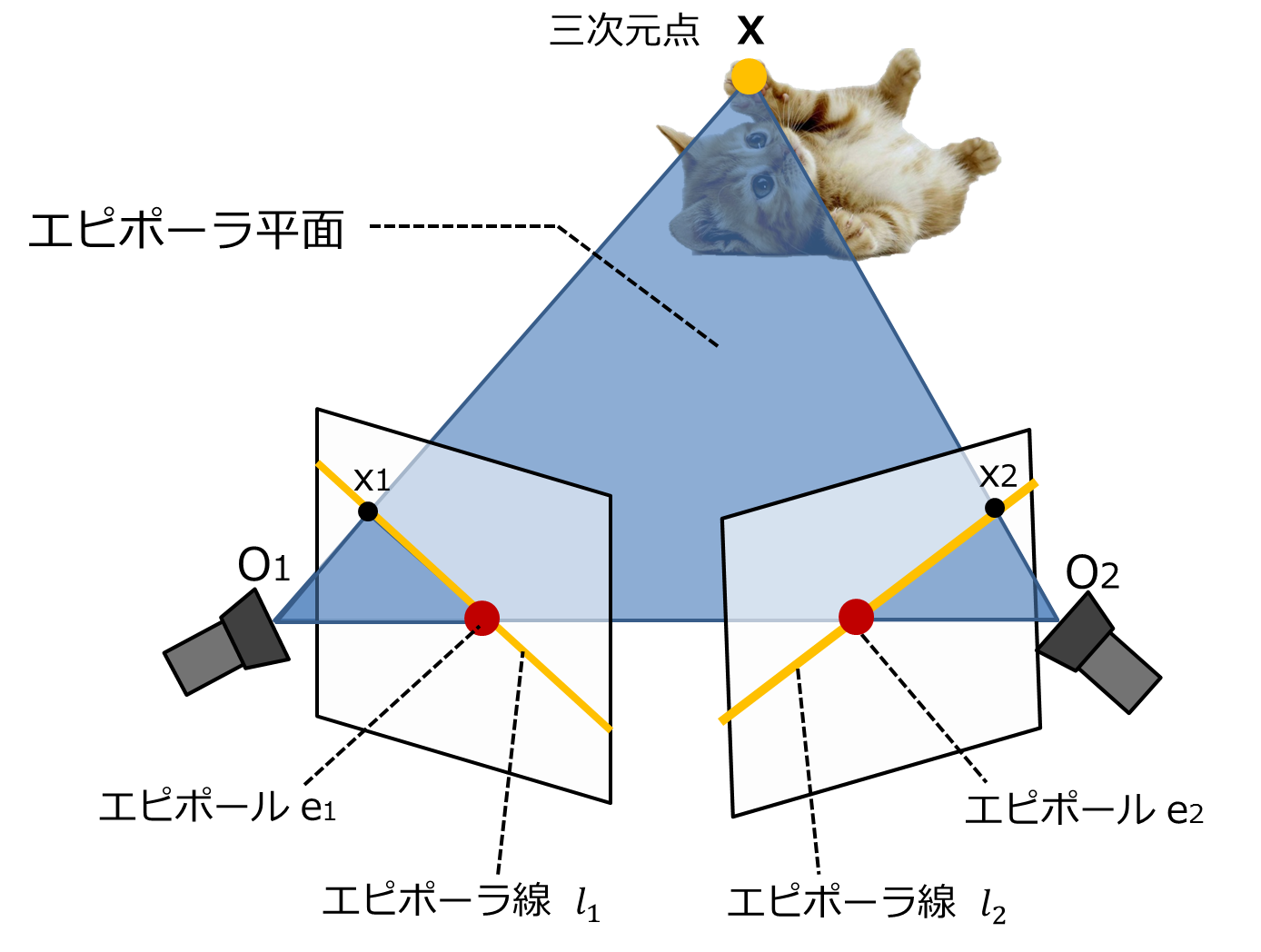
二つのカメラの光学中心を$O_{1}$, $O_{2}$としたとき、三次元点$X$, $O_{1}$, $O_{2}$の計3点を通る平面をエピポーラ平面と呼びます。図の青い平面です。 -
エピポーラ線 (図の黄色い線)
エピポーラ線とは、エピポーラ平面とそれぞれの画像平面とが交わる線のことです。
例えば三次元点Xが画像1上に点x1として映ったとき、同じ点Xが画像2上でエピポーラ線上のどこかに映ることを示しています。 -
エピポール (図の赤い点)
各画像すべてのエピポーラ線は、必ず1点で交わります。それがエピポールです。したがって、すべてのエピポーラ線がエピポールを通ります。この点は、他方の画像のカメラ中心を自分の画像に投影した点です。
-
基礎行列(Fundamental Matrix)
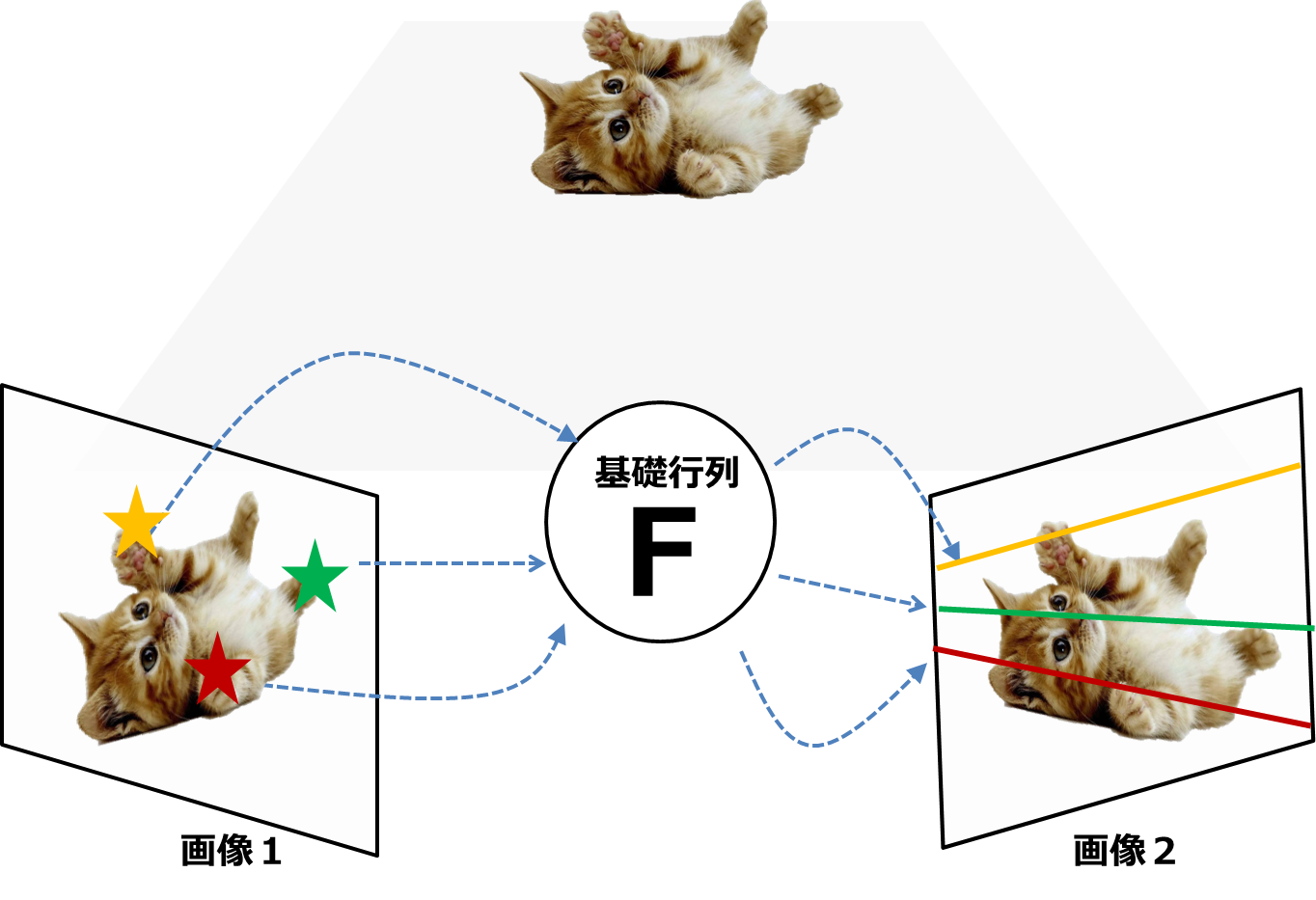
3x3の行列で、**カメラ内部・外部行列の情報を含んでいます。**また、ある画像上の点(0次元)を、別の画像上のエピポーラ線(1次元)にマッピングする役割をもちます。
この行列を推定できると、その後カメラ運動などを推定する際に利用できるので、この行列を正しく求めることがとても大事になります。次で詳しく見ていきます。 -
基本行列(Essential Matrix)
基礎行列と名前が似ていますが、基礎行列の親戚です。3x3の行列で、**カメラ外部行列の情報を含みます。**カメラ内部行列$K$を使って、$F$から$E=K_{2}FK_{1}$と変換できます。
基礎行列F
エピポーラ拘束式の登場
$x_{1}$と$x_{2}$が対応点の場合、すべての対応点$x_{1}$, $x_{2}$に関して、以下の関係が成り立ちます。
\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0
$F$は基礎行列を呼ばれていて、3x3行列です。
$x_{1}$, $x_{2}$は画像座標系での対応点の座標を同時座標系で表した3次元ベクトルです。
この式は二つの画像の対応点に拘束関係があることを示しています。この式をエピポーラ拘束式といいます。 視点が決まれば、画像1で見つけた対応点が、画像2でどの辺にあるかということが決定してしまう(=拘束)います。そしてこの拘束式は2つの視点のみに依存しており、3次元シーンには一切依存していません。
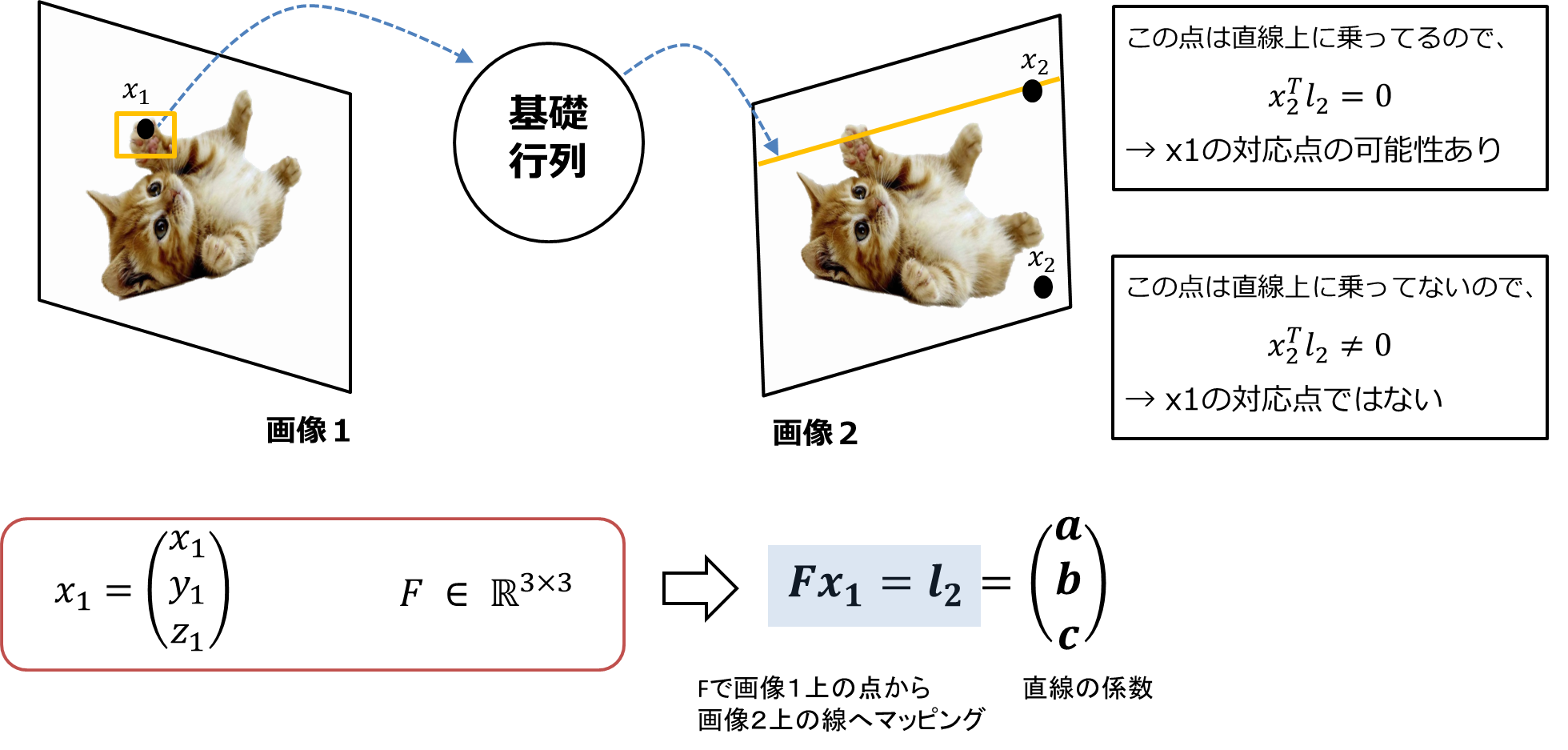
では、本当に$\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0$は成立するか確認します。
$x_{1}$は画像1上の点なので、$x_{1}=(x_{1},y_{1},z_{1})^{T}$とあらわされます($z_{1}$は1)。
一方、Fは3x3行列なので、$x_{1}$との積である$Fx_{1}$は3次元ベクトルをあわらしています。このベクトルを$Fx_{1}=(a,b,c)^T$とします。
この$Fx_{1}=(a,b,c)^T$が画像2上のエピポーラ線の係数です。そしてこの係数と、エピポーラ線上にあるx2をかけると、直線の方程式である$ax+by+c=0$を満たすことを示しています。つまり、$\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0$が成立します!
逆に、もし$x_{2}$を代入した結果が0でないならば、その点$x_{2}$はx1の対応点でないとも言えます(下図参照)。
画像1内の点$x_{1}$の画像2での対応点$x_{2}$を探す場合に、画像2内の画像全体を探すのではなく、$x_{1}$を画像2上に投影したエピッポーラ線$l_{2}$のみ探せばよいので計算コスト・誤対応率が下がります。
ちなみに、上式 $\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0$ は、画像1上の点$x_{1}$を画像2に直線として写像した場合をあらわしています。
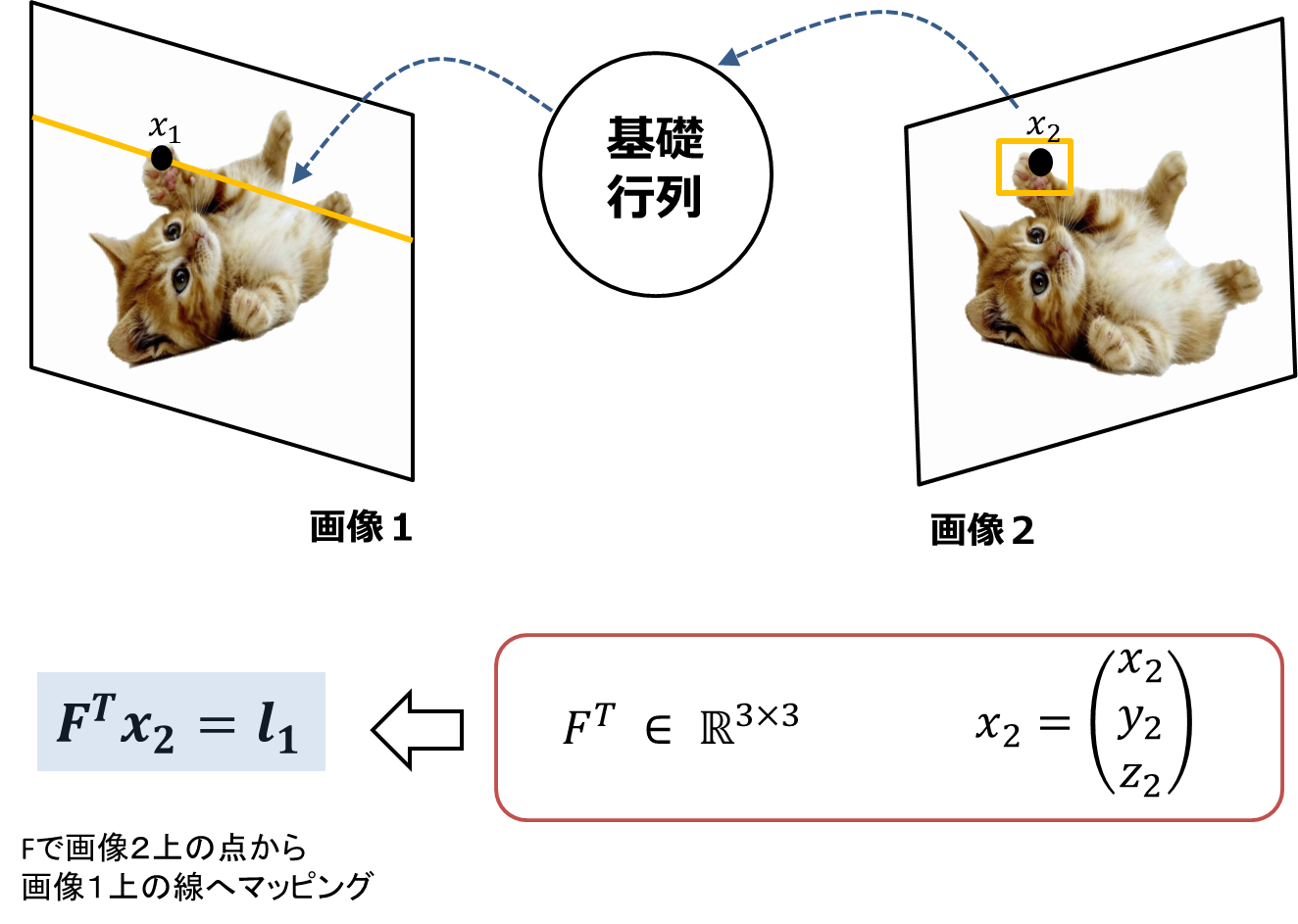
その反対に、画像2上の点$x_{2}$を画像1に直線として写像した場合は次式のようになり、両辺に転置をかけただけなので、数学的には同じものです。( $(\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}})^{T}=$次式 )
\boldsymbol{x_{1}^{T}}F^{T}\boldsymbol{x_{2}} = 0
$x_{1}$と$x_{2}$の位置が入れ替わり、Fが転置になっているのがポイントです。
1. Fを求める
じゃあどうやってFをもとめるのか?そのための代表的な手法がいくつかあります。
-
8点アルゴリズム
対応点を8点以上使ってFを推定する。SVDを使って最小二乗法で解く。実用ならば正規化8点アルゴリズムを使うこと。 -
正規化8点アルゴリズム
8点アルゴリズムの改良版。正規化処理として、原点を対応点の点群の重心にもっていき、重心から各対応点までの平均距離を$\sqrt2$にすることで、精度が格段に上がる。
[正規化8点アルゴリズム実装]
(http://www.peterkovesi.com/matlabfns/Projective/fundmatrix.m)
正規化実装 -
代数学的なコスト最小化(繰り返し)
正規化8点アルゴリズムより精度がよい。 -
観測点と推定点との距離の誤差の最小化
上の方法で初期値としてFを与えたあとに、いったんXの位置を計算してそれを画像上に投影する。観測点と推定点との距離(誤差)をコスト関数として最小化する。Gold Standard Algorithmと言われていて、もっとも精度が高い。
また、2つのカメラ行列が既知であれば、そこから求めることもできます 実装
8点アルゴリズム
一番基本的な8点アルゴリズムの概要を紹介します(詳しい実装は上記リンクを参照してください)
エピポーラ拘束式$\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0$により、各対応点iについて以下の式が一つ得られます。
ここで未知変数はF行列なので、Fについてまとめてあげて、方程式Af=0の形でfについて解きます。
ここで、Fは3x3の行列ですが、スケール不定なので実質8点の対応点があれば解くことができます。「8点アルゴリズム」の名前はここから来ています。
SVDで分解したあと、Fがランク2であることを利用します。Σの対角成分の最小特異値を0にして解けば、Fの精度が上がります。
下図の左がランク2である制約をかけなかった場合、右がランク2である制約をかけた場合です。
2. Fからカメラ行列を求める
ではなぜFを求めたのか、それはFからカメラ行列Pをを求めることができるためです。
さきほど述べたように、Fは内部カメラ行列と外部カメラ行列を含んでいます。なので、Fを内部・外部カメラ行列に分解してあげれば、Fからカメラ行列を推定することができます。
ただし、カメラキャリブレーションを事前に行っているかどうかで、推定の精度が変わってきます。カメラ内部パラメータが未知の場合は、Fからは射影変換までしか推定できません。
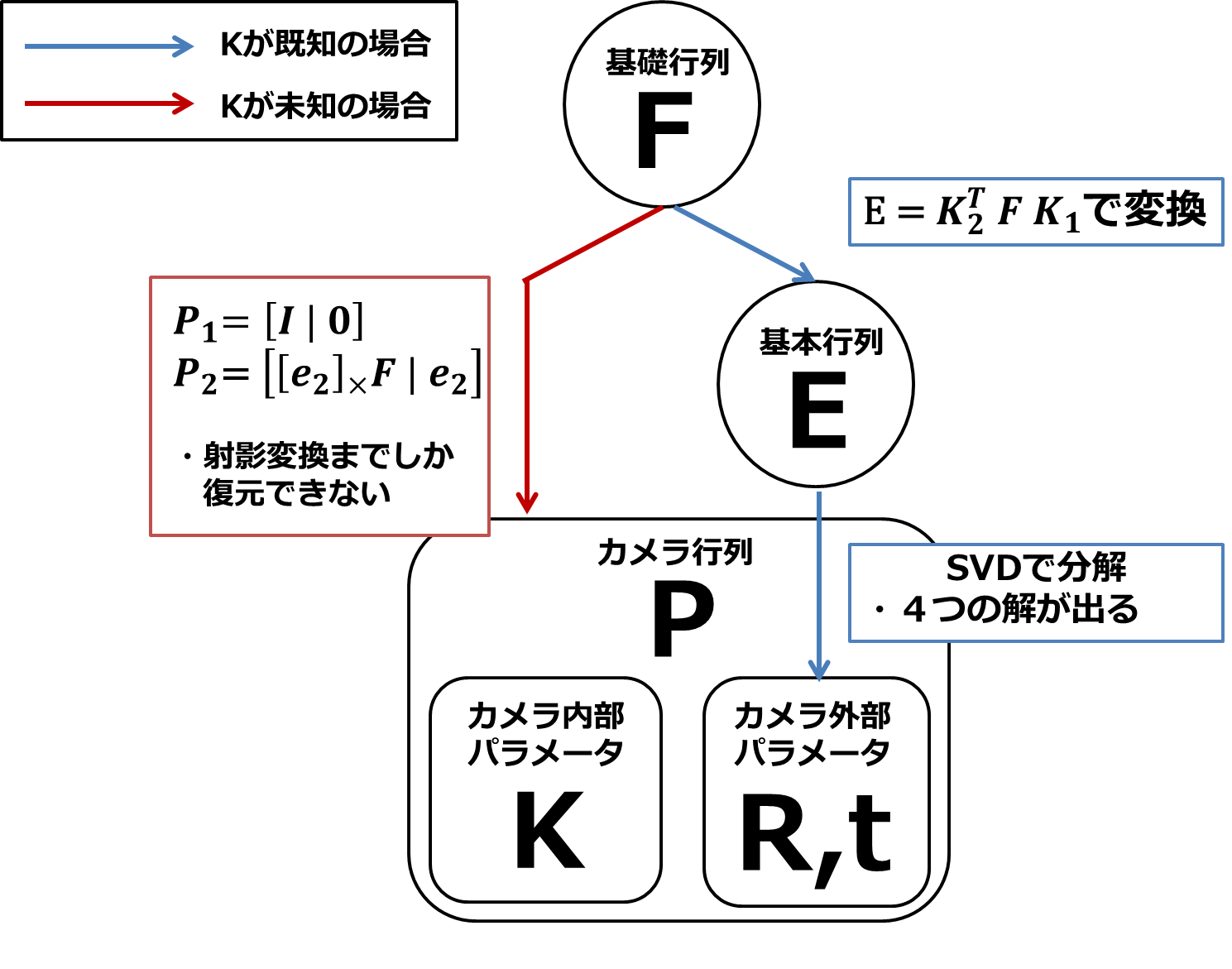
Fからカメラ行列を推定するまでの処理の流れは下図のようになります。
カメラがキャリブレーション済みでない場合
カメラがキャリブレーション済みでない場合、つまりカメラの内部パラメータが未知の場合は、カメラ内部・外部パラメータの両方を推定しなくてはいけません。この場合は、カメラ行列は射影変換までしか推定できません。
通常、PからFを一つに求めることはできますが、その逆の、FからPを一つに求めることはできません。なぜなら、射影変換された2組の画像の基礎行列は同じであるからです。
例えば、カメラ行列(P,P′)のFと、カメラ行列(PH, P′H) のFは同じになります。
カメラ行列$P_{1}$, $P_{2}$は次のようになります。×は外積です。
P_{1}=[I|0] かつ P_{2} =[[e_{2}]×F|e_{2}]
カメラがキャリブレーション済みの場合
カメラがキャリブレーション済みの場合は、カメラ外部パラメータのみ推定すればよいことになります。併進方向のスケールを除いて、すべてのパラメータを推定することができます。Fは射影変換のあいまいさがありますが、Eは四つの解をもつというあいまいさがあります。
まず、Fから$E=K_{2}FK_{1}$を使って、基礎行列Eを求めます。
次に、EをSVDで分解します。Eはdet(E)=0で、0でない特異値が等しくその大きさが不定なので、Σの対角成分を(1,1,0)と書くことができます。つまり、SVDで以下のように分解できます。
E=Udiag(1,1,0)V^{T}
$u_{3}$は$U$の3列目のベクトルとし、
W = \begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{pmatrix}
とすると、最終的に、カメラ行列は以下4つの解が出てきます。

これらのうち、一つだけがカメラの前方にシーンを持ちますので、(a)が正しい解です。(下図)

文献[1]より引用。
3. 3D世界を再構築する
カメラ行列Pが求まりました。ではいよいよ3次元世界を再構築してみましょう。
三角測量
三角測量は、2つの視点から得られる下記のカメラ変換式を同時に満たすXを推定します。

文献[1]より引用。
カメラ行列が$P_{1}$, $P_{2}$のカメラ変換式から
\lambda_{1}x_{1} = P_{1}X
\lambda_{2}x_{2} = P_{2}X
なので、行列表現すると、
\begin{bmatrix}
P_{1} & -x_{1} & 0 \\
P_{2} & 0 & -x_{2}
\end{bmatrix}
\begin{bmatrix}
X \\
\lambda_{1}\\
\lambda_{2}
\end{bmatrix}
=0
となります。
これもAx=0の形なので、xをSVDで解くことで3次元Xを復元できます。
実装
- ykoga/cv_tutorial_epipolar (OpenCV)
- OpenCV3.1(2015/12リリース)からStructure From Motion機能が入ったsfmモジュールが追加されました