ブロックチェーンや暗号通貨に関する前提知識は不要です。お気軽にお読みください。
この記事は、「全人類の口座残高を管理する――(1) Bitcoinの場合――」の続きです。
導入:「残高」はあったほうが良い
ブロックチェーンで「残高」を管理しないことの嫌な点
Bitcoinのコアプロトコルが扱うブロックチェーンに刻まれているのは、全世界の全「取引」の履歴であって、そこに「残高」の情報は直接含まれていません。
論理的にはそれで構わないのですが、現実のBitcoinネットワークのノードは、新たな取引の正当性(ちゃんと取引の原資があること)を妥当な時間で検査するため、「UTXOデータベース」というものを管理する必要があります。この「UTXOデータベース」は、実質的にはブロックチェーンから派生的に計算される「残高」情報のようなものです。
この「UTXOデータベース」を管理する実装は容易というわけでもなく、またこのようなコアプロトコルと実装との乖離は、前の記事で触れたように、様々に面白くない帰結をもたらします。
だったら「残高」をブロックチェーンで合意すれば良いのでは?
どうせそういうことなら、ブロックチェーンにはじめから「残高」の情報も含めてしまって、それを合意対象にすれば良かったのではないでしょうか?
「BitcoinのブロックにUTXO集合の情報も含めることにして、それを合意対象にすれば良いと思うのですが、これはすごく難しいことだと聞きました。具体的にどう難しいんですか? 解決する方法はないんですか?」
実際、ブロックの正当性検査の一部として「残高」の引当可能性検査を行うことは必要であり、またブロックチェーンから「残高」を導出する時間計算量が小さいわけでもなく、さらにブロックチェーンに合わせて「残高」情報を維持管理する実装もそれなりに難しい以上、ブロックに「残高」情報も含めてコアプロトコルで合意しとけよ、という方向性には否定できない正しさがあります。つまりこの質問は良い質問だと思います。
この記事では、Ethereumの実装を引き合いに出して、この質問に答えを提示しようと思います。
結論を先回りして言うと、なかなか芸術点が高いデータ構造のアイディアが出てきて、解決が難しそうだった問題が鮮やかに解決されますよ。
「残高」を合意することの困難
予備的な考察
ブロックチェーンに「残高」情報を含めて合意することにメリットがある、というとき、それは個々のブロックに、全人類の口座残高情報を含めることを意味するはずです。
「当該ブロックに含まれる取引によって残高が変化した口座についてのみ、その残高を当該ブロックに含める」というようなアーキテクチャでは、「ブロックチェーンとUTXOデータベースとの二元性」のような構造上の問題は解消されませんし、「ブロックチェーンの巻き戻しに伴うUTXOデータベースへのパッチ適用」のような感触の悪い実装もなくせません。
あくまでも、個々のブロックに、その時点で存在するすべての状態を含めることが必要なのです。
全人類の残高情報を含める、というとき、本当は「口座A1の残高は100BTC、口座A2の残高は50BTC……」というような具体的な口座残高の集合を直接ブロックに含められれば、「ブロックN時点への巻き戻し」が楽なのでありがたいのですが、さすがにそれは1ブロックの容量という点で無理があります。
BitcoinやEthereumのようにグローバルでシングルトンなネットワークにおける口座数は、何十億件や何百億件になってもまったく不思議ではありませんから。(また、Ethereumの機能は暗号通貨の授受だけではないため、保存したい「状態」情報は「残高」の他にも多くあるのです。)
ですから、ブロックに含めて合意するのは、「全人類の口座残高情報の集合から算出されるダイジェスト値」で我慢しておくのが妥当なところでしょう。
ブロックNに含まれるこのダイジェスト値について合意できれば、ブロックNまでの全取引が行われたあとでの、全人類のあらゆる口座の残高すべてについて、コアプロトコルで直接合意できた、ということになるわけです。
この場合、あとから「ブロックN時点への巻き戻り」が必要になった時のために、各ノードは、そのダイジェスト値に対応する残高データベースのスナップショットを、だいじに取っておく必要があることになります。
スナップショットの世代数によっては、ものすごく容量を食うんじゃないか、こういう容量を食わないように、BitcoinのUTXOデータベースは、Undoパッチという差分形式で巻き戻り用ログを管理しているんじゃないか、とか気になる人はなるでしょうが、その話には後で触れます。
ダイジェスト値の計算も容易ではない
ここまではまあいいと思いますが、このような「ある時点における全人類の口座残高の集合から算出されるダイジェスト値」を計算する方法も、それほど自明とは言えません。
ナイーブな実装では、ブロックを1個生成するたびに、そしてブロックを1個検証するたびに、それを実行するノードは、何十億件、何百億件になるかもしれない全人類の口座情報を決まったやり方でソートして、その内容を1個1個ダイジェスト計算機に入力しなければならないことになります。
全口座数が数十億とか数百億といった程度に巨大であり得る、という前提のもとでは、とうていこのような計算負荷の発生を受け入れることはできません。では、どのようなうまいアーキテクチャがあり得るか?
Ethereumによる解決:Merkle Patricia Tree
先ほど、ナイーブな実装ではダイジェスト値を計算するたびに全人類の口座情報をソートしてダイジェスト計算機に入力する必要がある、と書きましたが、それはさすがにナイーブすぎる、と思われた方も多いでしょう。
まず、口座情報を保存するためのデータ構造を何らかの順序付きの木構造にすれば、必要になるたびに毎回ソートする必要はなくなりそうです。
もう一歩考えを進めてみると、全口座情報のダイジェスト値を計算する際にも、その順序付きの木構造を活かして、部分木(subtree)ごとのダイジェスト値を集約する形で(つまりダイジェスト値のダイジェスト値を再帰的に)計算すれば、口座情報が更新されたときに、その更新された口座情報に関係のある木構造のノードだけを計算し直すことで、効率よく全口座情報のダイジェスト値を計算することができそうです。このように部分木を集約する形でダイジェスト値を計算するためのデータ構造/アルゴリズムをMerkle Treeと言い、Bitcoinの「取引」のダイジェスト値計算のためにも利用されています。
このようなアイディアに基づいて、
- 1個の口座情報が更新された際に、全口座情報を代表するダイジェスト値を、少ない時間計算量で計算し直すことができる。
- キー&値の更新にかかる時間計算量のオーダーが、全エントリー数に対して大きくない。
- キーによる値の探索にかかる時間計算量のオーダーが、全エントリー数に対して大きくない。
- 空間効率が、全エントリー数に対して高い。
- これらの特性を維持したまま、全エントリーの状態を、任意の時点のスナップショットに簡単に巻き戻すことができる。
といった条件をすべて満たすデータ構造として考案されたのが、Ethereumにおけるコンセンサスおよび状態管理の中核となるデータ構造であるMerkle Patricia Treeです。
数十億~数百億件の口座残高を高速に保存・探索することができ、またすべてのエントリーの内容を反映したダイジェスト値を高速に計算することができ、さらに好きな時点に状態を巻き戻せて、空間効率も高い、という無い物ねだりに全部答えてくれる夢のデータ構造ですから、以下でこれについて詳しく見てみましょう。
Ethereumが、全人類の口座残高をはじめとする多数のデータを保管するために利用するデータ構造は、基本的には、Prefix Treeの一種であるPatricia Treeです。
Prefix Tree
Prefix Treeは要するに、keyとvalueとを対応させる連想配列ですが、keyを要素の並びに分解して、keyを構成する個々の要素を、木構造のノードに対応させる点に特徴があります。(このデータ構造は、Trieという名前でも知られています。)
Ethereumでは、keyを4ビット(=1ニブル)を要素とする並びに分解して、16分木を構築しています。1ビットは2値、1バイトは256値であるのと同様、1ニブルは16値だから、16分木になるのです。
たとえば、Ethereumのユニットテストのテストケースにもなっている単純な例を見てみましょう。
まず、「dog」という文字列がkeyで、「puppy」という文字列がそれに対応するvalueだとします。ここでkeyである「dog」を、まずバイト列に変換します。ASCIIバイト列をとれば、[0x64, 0x6f, 0x67]の3バイトとなります。これをさらにニブルに分解すると、[6, 4, 6, f, 6, 7]の6ニブルとなります。(実際には、「ニブルの並びの終わり」を表す終端記号も必要なのですが、この記事では無視します。)
次に、「do」という文字列が別のkeyで、「verb」という文字列がそれに対応するvalueだとします。このkeyを上と同様にニブルに分解すると、[6, 4, 6, f]の4ニブルになります。
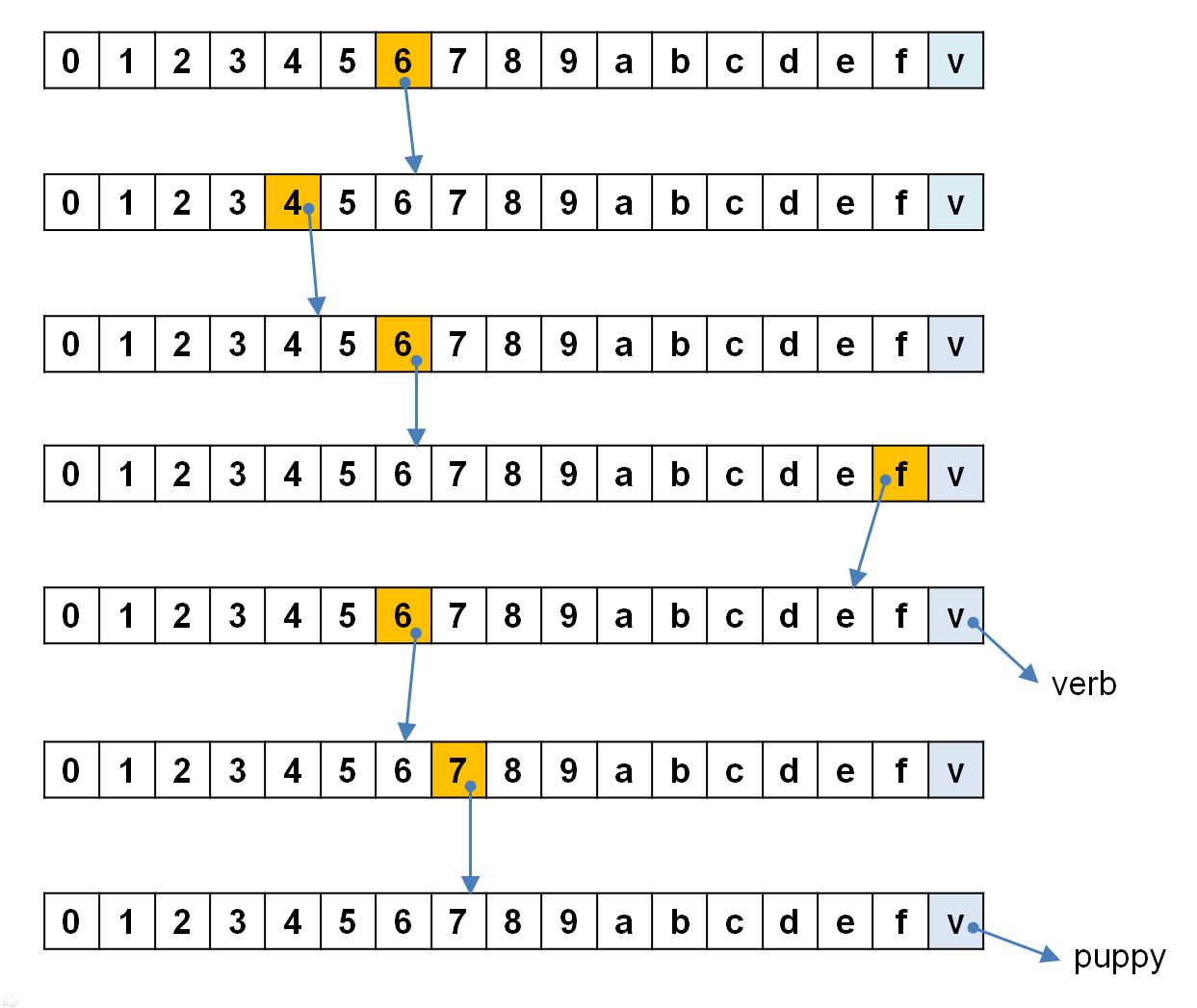
これら2つのエントリーを持つ16分木のPrefix Treeの構造を図示すると、以下のようになります。
dog [6,4,6,f,6,7] -> puppy
do [6,4,6,f] -> verb
17マスの長屋みたいなものが、それぞれ16分木Prefix Treeのノードです。個々のノードは、最大16個の子ノードと、最大1個の値を持ちます。ルート要素から出発して、キーを構成するニブルを辿りきった先にある値が、そのキーに対応する値になるわけです。
この例でもそうですが、共通のプレフィックスを持つデータは、空間的にも共通のノードで表現されるため、エントリー数に対する空間効率が良くなっていることがわかるでしょう。16分木の構造を構築するオーバーヘッドは大きいですが、エントリー数が莫大になったときには、重複するプレフィックス部分が新たな空間を消費しない、ということがメリットになるのです。
また、検索および更新の時間計算量が、key長に比例するようになっており、データ件数に相関しないこと、そして、key長に比例して発生する操作は単純なニブル値の比較であって、文字列比較のような重い操作ではないことも分かると思います。
Patricia Tree
ここにさらに、時間・空間両面でのショートカットを加えたのがPatricia Treeです。
Patricia Treeでは、他のエントリーと共有されないあるエントリー固有のノードの経路を、馬鹿正直に1個1個ノードにせず、その経路をショートカットした1ノードによって表現します。
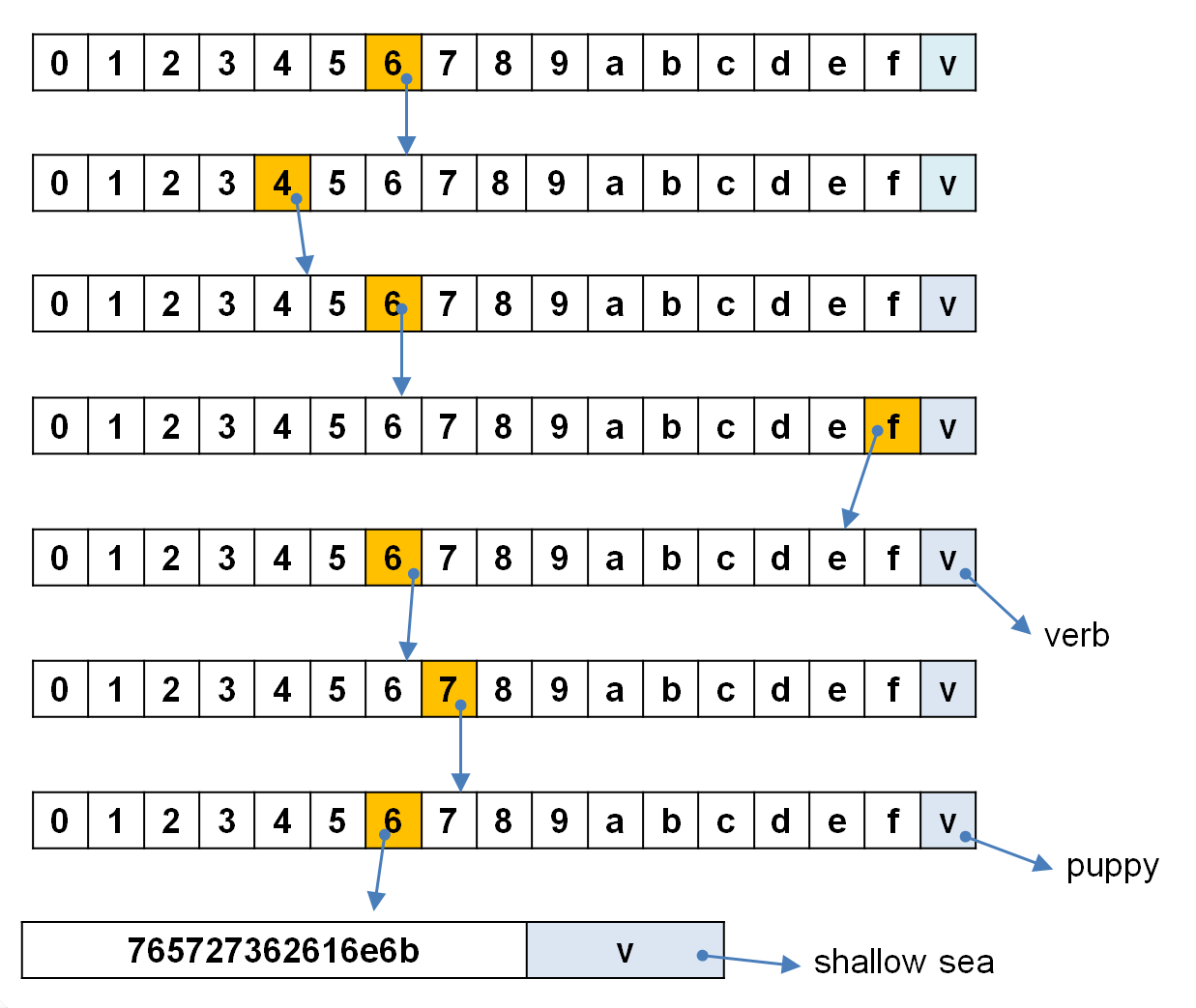
たとえば、上の木構造に「doggersbank -> shallow sea」というエントリーを加えて3エントリーの構造を作る場合、キーの先頭の「dog」6ニブルまでは、既存のエントリーと経路を共有できますが、そこから先の「gersbank」16ニブルは、このエントリーでしか利用されない経路です。これをいちいち16ノードかけて表現するのでは時間も空間ももったいないので、ショートカット用の1ノードを作って表現するのです。
doggersbank [6,4,6,f,6,7,6,7,6,5,7,2,7,3,6,2,6,1,6,e,6,b] -> shallow sea
上の図で、「do」の部分は3エントリーすべてに共通する経路、「dog」の部分は2エントリーに共通する経路ですが、そこから先の「gersbank」に対応する「6,7,6,5,7,2,7,3,6,2,6,1,6,e,6,b」の16ニブルは「doggersbank」の1エントリーによってのみ利用される経路なので、その部分をショートカットの1ノードによって表現しているのです。
この3エントリーのPatricia Treeにさらに別のエントリーが追加登録されて、「gersbank」の部分も他のエントリーと共有できることになった場合、このショートカットノードのうち必要な部分は、17マスの長屋のような通常ノードに変換されることになります。このような実装は、むろん面倒でバグを生みやすいものですが、この種の難しさは、ユニットテスト等で十分に制御できる難しさだと言えるでしょう。
Merkle Patricia Tree
以上のPatricia Treeに、さらにダイジェスト値の管理機能を加えたデータ構造、もしくは、Patricia Treeをダイジェスト値の管理によって実装したデータ構造が、Merkle Patricia Treeです。これが、「残高」をはじめとする多数の情報を効率よく保管し合意するためにEthereumプロジェクトで発明され、利用されているデータ構造です。
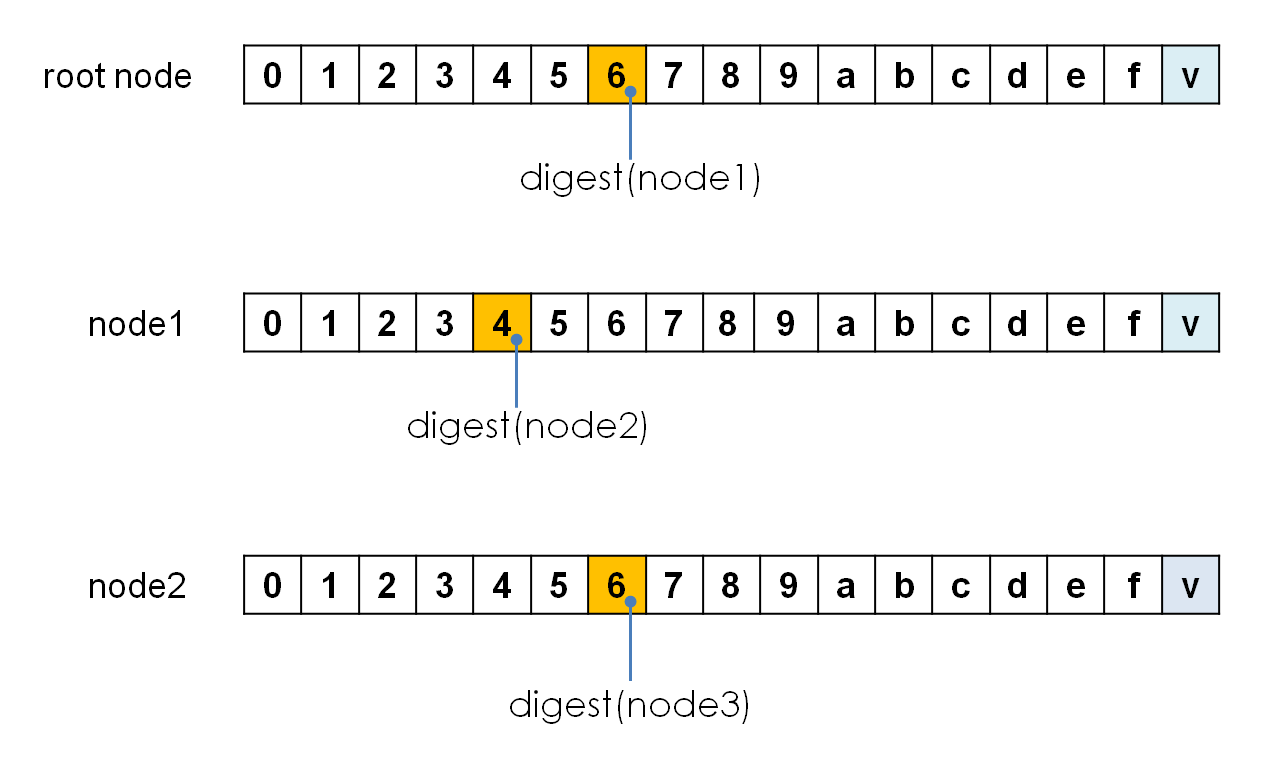
これまでの図では、ノード間の参照関係をなんとなく矢印で表現してきました。木構造をメモリ上に展開するという前提では、このような矢印はポインタによって実装されるのが自然でしょうが、巨大な木構造の全体をメモリ上に展開できるとは限りません。また、仮にメモリ上に展開できるとしても、その木構造の管理するデータが重要なものであるならば、その全データを揮発性ではないデータストレージに永続化しておく必要があります。
木構造をデータストレージに永続化する設計には様々なやり方があり得るでしょうが、Merkle Patricia Treeでは、ダイジェスト値を使ってこの参照関係を表現し、永続化します。つまり、木構造の個々のノードは、そのノードを決まったやり方でシリアライズしたバイト列のダイジェスト値を識別子として持ち、そのダイジェスト値によって参照されるのです。
Ethereumでは、ノードのシリアライズには「RLP」という独自の方式を使い、ダイジェスト計算のアルゴリズムには256ビットKeccakを使い、永続化にはLevelDBを使っていると思いますが、そのどれも、特に本質的に重要というわけではありません。シリアライズの方法も、ダイジェスト計算のアルゴリズムも、永続化に利用するデータストアも、違う実装を採用しても本質的な構造は何ら変わりません。
Merkle Patricia Treeを更新するたびにダイジェスト値を計算するとした時、その時間計算量は、key長に比例して、データ件数には相関しないことがわかると思います。
また空間面でも、Prefix Treeと同様に共通の経路は共有され、Patricia Treeと同様のショートカットが効き、あるノードそれ自身の内容が変更されない限り、他のノードの更新に付き合ってノードが複製されるといったこともありません。
ダイジェスト値の集約
このアーキテクチャによって、あるノードのダイジェスト値を計算することは、そのノードをルートとする部分木のダイジェスト値を集約して計算することと同義になり、最終的にルート要素のダイジェスト値を計算すれば、それが、巨大なPatricia Treeの全要素を代表するダイジェスト値になることが保証されるのです。これが、Merkle Patricia Treeの第一の眼目です。
任意時点への巻き戻しの実現
さらに素晴らしいことに、このようにダイジェスト値によって個々のノードを参照し、またダイジェスト値とノードとの対応関係を永続化しておけば、それだけで、任意時点への巻き戻しが実現できたことになるのです。
ある時点におけるMerkle Patricia Treeのルート要素のダイジェスト値を、ロールバック用のポイントとして記憶した、と考えてください。その後、そのMerkle Patricia Treeにいかに複雑で大量の更新が加えられたとしても、記憶したダイジェスト値1個があれば、その時点のルートノード(がシリアライズされたバイト列)をデータストレージからロードすることができます。ルートノードには、最大16個の子ノードのダイジェスト値が記録されています。そして、それらのダイジェスト値を元に、任意の子ノードをロードすることができるわけですから、結局のところ、最上位のルートダイジェスト値1個を覚えておけば、それでそれに対応する時点のMerkle Patricia Treeの全体をいつでも探索することができ、その時点のMerkle Patricia Treeに対して任意の更新を加えることもできるのです。
まとめ
この Merkle Patricia Tree は、単純な実装方法として見た時に、Bitcoin の個々のノードが行っている「UTXOデータベースとUndoファイルの管理」よりも優れています。時間計算量および保存容量が、バックエンドとなるデータストアの実装を考慮に入れてもなお、総エントリー数に対して小さいオーダーで済むということも大きなメリットですが、任意時点のスナップショットへの巻き戻しが容易であることも、それに劣らず素晴らしい。
審美的な観点からは、「時間・空間効率の良い多数エントリーの保存および探索」という困難な要件と、「全エントリーを代表するダイジェスト値の高効率な計算」というやはり困難な要件と、「ブロックチェーンのフォークに対応したロールバックの実現」というまたしても困難な要件を実現するためのすべての手段が、あたかも相互の要件を実現するための補助手段になっているかのように密接に結びついている、という美しさを指摘しておきたいと思います。
時間・空間の計算量を総エントリー数に相関しないオーダーに抑えられるのはPrefix Treeの手法を採用したからであり、Prefix Treeの個々のノードを immutable な形で効率よく保管できるのは、Merkle Treeの手法を採用してダイジェスト値の計算を可能にしたからこそです。そしてMerkle Treeによって実現された再帰的なダイジェスト値の管理が、そのまま任意時点への巻き戻しを実現するための手段にもなっているのです。
さらに状態管理に関するEthereumの仕様についても、プロトコル仕様とノードの実装とがぴたりと表裏一体になった美しさがあると思います。Ethereumのコンセンサス・プロトコル自体はノードの実装からは独立していますが、しかしEthereumのプロトコルに妥当な時間計算量で準拠できる実装は、このMerkle Patricia Tree以外に考えられません。これは、Ethereumのyellow paperにも書かれている通りです。
仕様が実装アーキテクチャをおのずから示唆し、そしてその示唆されるアーキテクチャが優れたものであるならば、システムのその部分にはまず大きな懸念はないとしたものです。
さらにこのような相互関係は、ブロックチェーンとEthereumとの間にも見られると思います。ブロックチェーンという発想それ自体に、チューリング完全なプログラム実行基盤の構築と、それに応じた膨大な数の「状態」(もはや「残高」に限らない!)の管理という応用の可能性は、すでに萌芽として含まれていたはずです。Bitcoinのプリミティブなスクリプティング機能からも、中本哲史氏がそのようなアイディアを持っていたことは、十分にうかがい知ることができるでしょう。
EthereumのMerkle Patricia Treeによる状態管理の実現は、そのような可能性に対して、ふさわしい具体的な形を与えたものだったのだと思います。