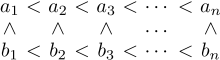カタラン数を語らん

TeX ＆ LaTeX Advent Calendar 2014の19日目の記事として投稿します。
昨日はzr_tex8rさん，明日はTeXゼミさんです。

カタラン数とは

「カタラン数を語らん」というなんともベタでアレなタイトルをつけてしまいましたが，さっそく定義します。

カタラン数の定義

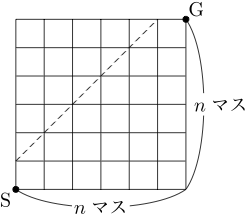
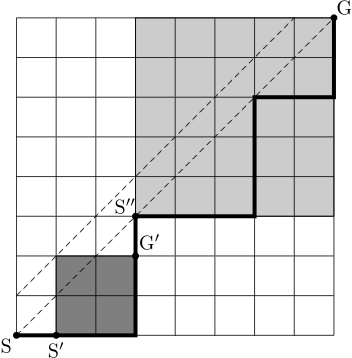
この図において，点 $\mathrm{S}$（スタート）から点 $\mathrm{G}$（ゴール）までの最短経路のうち，点線に触れないようなものの数をカタラン数といい，$c_n$ で表します。

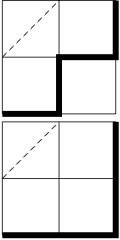
例えば $n=2$ なら下のようになり，$c_2=2$ となります。

また $n=3$ なら下のようになり，$c_3=5$ となります。

最初の6つのカタラン数を列挙しておくと，$c_1=1$，$c_2=2$，$c_3=5$，$c_4=14$，$c_5=42$，$c_6=132$ となります。

また，便宜上，$c_0=1$ と定めます。

カタラン数の具体的な表記

実はカタラン数 $c_n$ は具体的に

\frac{_{2n}\mathrm{C}_n}{n+1}

と表すことができ，その導出方法は難関大を目指す高校生にとっては必須事項です。ただ，今回の記事にはあまり関係しないので，割愛します。

それにしても，「点線を通ってはいけない」という条件がなければ $_{2n}\mathrm{C}_n$ 通りであるところが，その $\displaystyle\frac{1}{n+1}$ 倍になってしまうとは，結構減るんですね。

カタラン数の例

まだTeXは出てきません。（強いて言えば図をTikZで作っているというくらい。）

カタラン数が現れる有名な例を2つ挙げておきます。

◯と×の並び

$n$ 個ずつの○と×，合計 $2n$ 個のものを横一列に並べる方法のうち，以下の条件を満たすようなものの個数は，カタラン数 $c_n$ になる。

条件：どこをとっても，それより左を見ると○の数が×の数よりも多いか等しい。

数字の入れ方

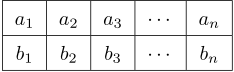
$n$ を自然数とするとき，$1$ から $2n$ までの自然数を，

の表に，

を満たすように入れる方法の数は，カタラン数 $c_n$ になる。

この他にもカタラン数が現れる例は多く存在します。Richard P. Stanley の “Enumerative combinatorics” (vol.1, vol.2¹)にはその例が実に66個掲載されており，また著者のサイトにはさらに多くの例があります。現在207個もの例があるそうです……！

ちなみに，この “Enumerative combinatorics” には，カタラン数のマニアのことを “Catalania” と呼ぶ，と書いてあります。

カタラン数の漸化式

カタラン数には漸化式があります。説明のために，$\mathrm{S}(0,0)$，$\mathrm{G}(n,n)$ となる $xy$ 座標を入れます。

$\mathrm{S}(0,0)$ からまず $\mathrm{S}'(1,0)$ に進みますが，その後どこかで必ず $y=x$ 上に乗ります（少なくとも $\mathrm{G}$ は $y=x$ 上）。はじめて $y=x$ 上に乗った点を $\mathrm{S}''(k+1, k+1)$ とすると，その直前には図の $\mathrm{G}'$ にいなければなりません。

$\mathrm{S}'$ から $\mathrm{G}'$ までの経路を考えると，$y=x$ に触れてはならないので，濃い網掛けで示した正方形（サイズ $k\times k$）でカタラン数を考えていることになるので，経路数は $c_k$ です。

そして，$\mathrm{S}''$ から $\mathrm{G}''$ までの経路は，薄い網掛けで示した正方形（サイズ $(n-k-1)\times (n-k-1)$）でカタラン数を考えていることになるので，経路数は $c_{n-k-1}$ です。

よって，はじめて $y=x$ 上に乗る点が $\mathrm{S}''(k+1, k+1)$ であるような経路は $c_{k}c_{n-k-1}$ 個あることになります。$k$ の範囲は $0\leqq k\leqq n-1$ なので，和を取って以下の漸化式を得ます。

c_n=c_0c_{n-1}+c_1c_{n-2}+c_2c_{n-3}+\cdots+c_{n-2}c_1+c_{n-1}c_0

これにより，効率的にカタラン数を求めることができます。

漸化式を使って示される例

上で挙げた◯と×の並びや数字の入れ方の例はあまりにも自明でした（ただの言い換えに過ぎない）が，次の例は対応があまり自明ではありません。

積の順序（カッコの付け方）

$n+1$ 文字の積の順序（カッコの付け方）は $c_n$ 通りである。

たとえば，$n=2$ であれば，3文字の積 $abc$ を計算するときのカッコの付け方は，$(ab)c$ と $a(bc)$ の $c_2=2$ 通りであり，$n=3$ であれば，4文字の積 $abcd$ を計算するときのカッコの付け方は，$(ab)(cd)$，$((ab)c)d$，$(a(bc))d$，$a((bc)d)$，$a(b(cd))$ の $c_3=5$ 通りです。

証明には漸化式を用います。$n+1$ 文字の積のカッコの付け方を $c_n'$ 通りとします。積を計算していく時の「最後の積」が左から $k+1$ 文字目と $k+2$ 文字目の間で起こるとします。すると，残りの部分のカッコの付け方は，$1$ 文字目から $k+1$ 文字目までの部分が $c_k'$ 通り，$k+2$ 文字目以降の部分が $c'_{n-k-1}$ 通りであり，$k$ を動かして

c'_n=c'_0c'_{n-1}+c'_1c'_{n-2}+c'_2c'_{n-3}+\cdots+c'_{n-2}c'_1+c'_{n-1}c'_0

となります。よって，数列 $c_n$ と数列 $c_n'$ は漸化式が同じで，第0項も等しいので，任意の $n$ に対して $c'_n=c_n$ となります。

多角形の分割

凸 $n+2$ 角形を，互いに交わらない対角線によって $n$ 個の三角形に分割する方法は $c_n$ 通りである。

これも，漸化式を用いて示されます。練習問題としましょう。

本題

ようやく本題です。

以上の内容を教えたとき，「カッコの付け方」と「経路」とがどう対応しているのか，という質問を受けました。たしかに，◯と×の並びや数字の入れ方の例では対応が自明だったのに対し，カッコの付け方が経路とどう対応するのかはあまり自明ではありません。しかし，漸化式を用いて個数が等しいことが示されているので，漸化式の成り立ちを考えれば対応は分かるはずです。

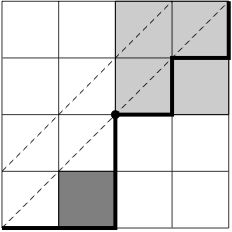
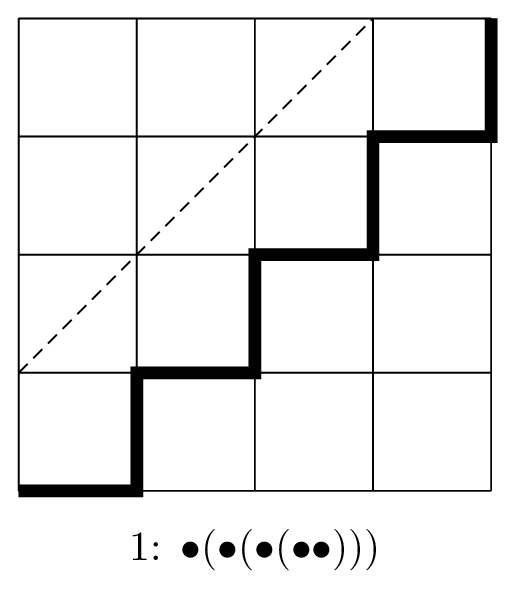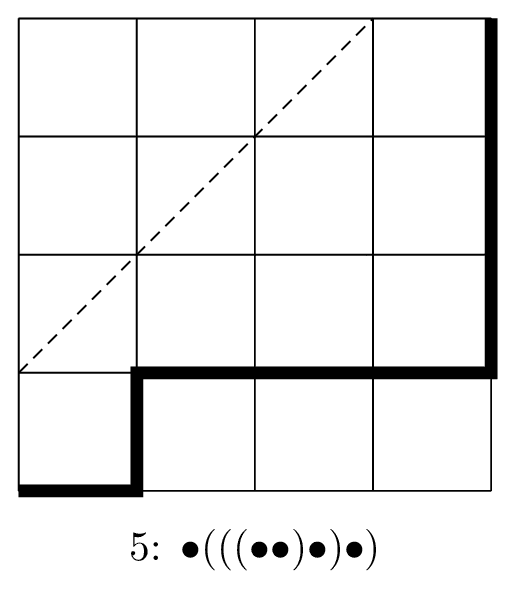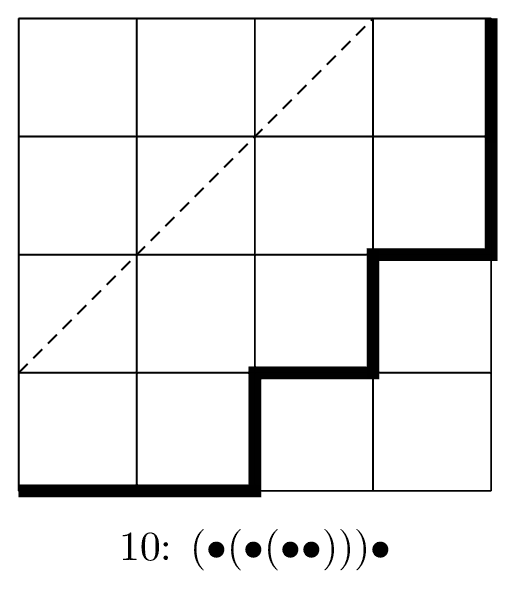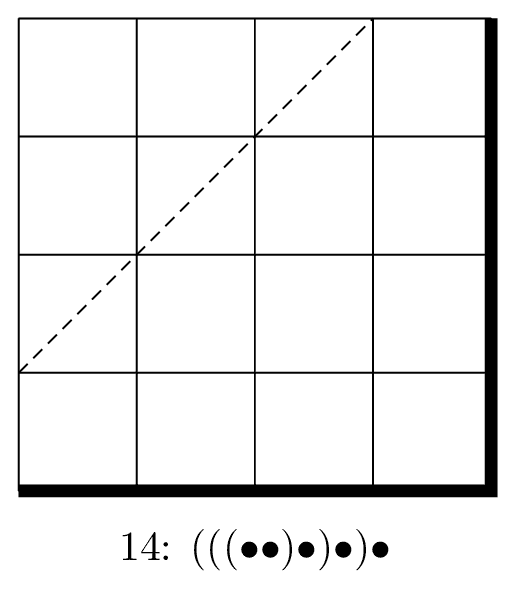
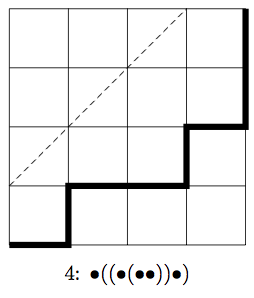
例えば，$n=4$ として，以下のような経路を考えてみます。対応するのは5文字の積のカッコの付け方です。

はじめて $y=x$ 上に乗る点は $(2,2)$ なので，5文字の積 $abcde$ に対しては，2文字目と3文字目の間が「最後の積」となり，とりあえず $(ab)(cde)$ とカッコが付けられます。その次に，残った2つの正方形（上の図で網掛けで示した正方形）での経路とカッコの対応を考えます。

**これはまさに再帰！**ということで，TeXで実装してみました。というのが本題です。

ソース

CatalanNumbers.tex

\documentclass{article}
\makeatletter

\usepackage{graphicx}
\usepackage{ifthen}
\usepackage{tikz}
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{3pt}

\def\e@namedef#1{\expandafter\edef\csname#1\endcsname}

\def\@startpath{\draw[line width = 3pt] (0,0) }
\def\drawUp{{ -- ++(0,1)}}
\def\drawRight{{ -- ++(1,0)}}

\def\@drawpaths#1{%
\@for\@pathData:=#1\do{%
\begin{tikzpicture}
\draw (0,0) grid (\drawpathssize-1,\drawpathssize-1);
\expandafter\@startpath\@pathData;
\end{tikzpicture}
}%
}

\def\bulletIfEmpty#1{%
\ifx#1\@empty $\bullet$\else (#1)\fi
}

\def\removeFirstComma#1{%
\edef\removeFirstCommaContent{#1}%
\expandafter\@removeFirstComma\removeFirstCommaContent\relax%
}
\def\@removeFirstComma,#1\relax{\def\removeFirstCommaResult{#1}}

\newcount\numa
\newcount\numb
\newcount\numc
\newcount\numd
\newcount\nume
\newcount\numf
\newcount\limitNum

\def\drawpaths#1{%
\limitNum=#1
\advance\limitNum 1
\@namedef{@paths0}{{{}}}
\@namedef{@braces0}{{{}}}
  \numa=1 \numb=0 \numc=0
  \loop
    \e@namedef{@paths\the\numa tmp}{}
    \e@namedef{@braces\the\numa tmp}{}
    \numd=\the\numb \nume=\the\numc
    {\loop
      \expandafter\@for\expandafter\@pathDataFirst\expandafter:\expandafter=\csname @paths\the\numd\endcsname\do{%
      \expandafter\@for\expandafter\@pathDataSecond\expandafter:\expandafter=\csname @paths\the\nume\endcsname\do{%
      \e@namedef{@paths\the\numa}{\csname @paths\the\numa tmp\endcsname,\drawRight\@pathDataFirst\drawUp\@pathDataSecond}
      \e@namedef{@paths\the\numa tmp}{\csname @paths\the\numa\endcsname}
      }
      }
      \edef\@tmpBraceFirst{\csname @braces\the\numd\endcsname}
      \edef\@tmpBraceSecond{\csname @braces\the\nume\endcsname}
      \expandafter\@for\expandafter\@pathDataFirst\expandafter:\expandafter=\@tmpBraceFirst\do{%
      \expandafter\@for\expandafter\@pathDataSecond\expandafter:\expandafter=\@tmpBraceSecond\do{%
      \e@namedef{@braces\the\numa}{\csname @braces\the\numa tmp\endcsname,\bulletIfEmpty{\@pathDataFirst}\bulletIfEmpty{\@pathDataSecond}}
      \e@namedef{@braces\the\numa tmp}{\csname @braces\the\numa\endcsname}
      }
      }
      \advance\numd 1 \advance\nume -1
    \ifnum\numd<\the\numa \repeat
    \removeFirstComma{\@nameuse{@paths\the\numa}}\par
    \global\e@namedef{@paths\the\numa}{\removeFirstCommaResult}
    \removeFirstComma{\@nameuse{@braces\the\numa}}\par
    \global\e@namedef{@braces\the\numa}{\removeFirstCommaResult}
    }
  \advance\numa 1 \advance\numc 1
  \ifnum\numa < \limitNum \repeat
%
\numf=0
\expandafter\@for\expandafter\currentBrace\expandafter:\expandafter=\csname @braces\the\numc\endcsname\do{%
\advance\numf1
\def\thisName{@braces\the\numc-\the\numf}%
\e@namedef{\thisName}{\currentBrace}%
}%
%
\numf=0
\edef\@tmpBraceFirst{\csname @paths\the\numc\endcsname}
\expandafter\@for\expandafter\@pathData\expandafter:\expandafter=\@tmpBraceFirst\do{%
\advance\numf1
\begin{tikzpicture}
\draw (0,0) grid ({\the\limitNum-1},{\the\limitNum-1});
\draw[densely dashed] (0,1) -- ({\the\limitNum-2},{\the\limitNum-1});
\draw ({(\the\limitNum-1)/2},-.5) node{\the\numf : \@nameuse{@braces\the\numc-\the\numf}};
\expandafter\@startpath\@pathData;
\end{tikzpicture}%
\par
}%
}
\makeatother
\begin{document}

\drawpaths{4}

\end{document}

（文字を「$\bullet$」で表しています。）

これで$c_4=14$ ページのPDFができあがります。\drawpathsの引数を変えればサイズが変わります。

previewパッケージを使っているので，TeX Liveのデフォルト状態では pdflatex，lualatex，xelatex でコンパイルできます。(u)platex + dvipdfmxでコンパイルするためにはZRさんのprdvipdfmx.defを入手してください。その場合はgraphicxパッケージとpreviewパッケージを\usepackageする際にdvipdfmxオプションを付けてください。

\usepackage[dvipdfmx]{graphicx}
\usepackage[dvipdfmx,active,tightpage]{preview}

アニメーションGIF化

このPDFを，ImageMagick の convert コマンドを使ってアニメーションGIFにしてみました。

convert -debug all -delay 30 -loop 0 -density 300 -alpha remove CatalanNumbers.pdf CatalanNumbers.gif

これで簡単に対応が調べられる！

これで，カッコの付け方と経路との対応が調べられるぞ！ということで調べてみると，「カッコ→経路」の対応は，どうやら

1. 左右を逆にする
2. 逆ポーランド記法にする（積を╳と書く）
3. 再び左右を逆にする
4. 「╳を右，●を上」として経路を描く（最後の●は無視する）

とするとうまく対応するっぽいです。例えば，「$\bullet((\bullet(\bullet\bullet))\bullet)$」なら，

1. $(\bullet((\bullet\bullet)\bullet))\bullet$
2. $\bullet\bullet\bullet\times\bullet\times\times\bullet\times$
3. $\times\bullet\times\times\bullet\times\bullet\bullet\bullet$
4. →↑→→↑→↑↑

となり，次の経路に対応することになります。

---

1. vol.2 はAmazon.co.jpでは書影画像がなかったためAmazon.comのリンクを貼りました。 ↩