はじめに
本 Tips では、UCI Machine Learning Repository(注1)のセンサーデータを使ったランダムフォレストによる分類をご紹介します。利用するセンサーデータは、モータの不良を11に分類した計測結果が含まれます。49列目に分類された結果が格納されています。1~48列目は電気信号のデータですが、詳しい列名などは不明です。
ランダムフォレストアルゴリズムとは?
ランダムフォレストは、分類、回帰、クラスタリングに用いられる機械学習のアルゴリズムです。アルゴリズム内では、弱学習器として決定木を使用して集団学習アルゴリズムに分類されます。この名称は、ランダムサンプリングされたトレーニングデータによって学習した多数の決定木を使用することに由来します。2001年に Leo Breiman によって提案されました。
このアルゴリズムでは、最初に複数の決定木を構築する処理から始めます。この処理は、一般的な決定木アルゴリズムと似ています。違いは、フルセットのデータから特徴量を特定する代わりに、分割した小さなランダムのサブセットのデータから特徴量を特定する点です。次に、同時に構築した複数の決定木のすべての平均を取って、最終モデルに帰結させます。これは、木の間の相関量を小さくして精度を高める事を目的にしています。木の数が多いとブートストラップ回数(注2)が増えるので、外れ値をサンプリングする確率が減り、外れ値の影響を受けにくくなるという考え方です。統計学的には、「(σ^2)の分散を持つ(Z_1, Z_2,…,Z_n)の数値があると仮定して、その平均{Z}は(σ^2/n)の分散を持つ」というシンプルな考え方になります。
ランダムフォレストが利用するデータの特徴量
ランダムフォレストでは、各決定木で異なるサンプルを使って学習します。これを実現するために、学習データをそのデータ数だけ重複サンプリング(ブートストラップ法による)し、それを学習サンプルとして決定木を学習させます。このとき、学習データのうち、平均で1/3ぐらいは学習に使われないそうです。この使われなかったデータを out-of-bag(OOB)といいます。cross validation の一種とも言える OOB 誤り率によって、学習結果の性能を評価することができます。
ランダムフォレストが分類を行う際には、データの特徴量を利用します。特徴量は、各決定木で OOB における誤り率を計算し、木あたりの平均を求めたものになります。この値の減少量を特徴量の重要度と近似的に表現します。また、特徴量を表現するのに、ジニ係数も使われています。ジニ係数による特徴量の重要度は、ジニ係数の大きいほど分割結果がばらつき、小さいほど分割結果がまとまっていることになる、という特性を利用しています。つまり、ジニ係数の減少量を特徴量の重要度と近似的に表現できます。
ランダムフォレストのパラメータチューニング
ランダムフォレストのパラメータチューニングは、作成する決定木の数(ntree)と、1つ1つの決定木を作成する際に使用する特徴量の数(mtry)の2つのパラメータで行います。決定木の数は、予測に用いる木の数を増やしていき結果が安定する数を利用すればよいだけです。特徴量の数は、特徴量の数がNの時√Nが推奨値となります。しかしながら、実際のところは最適な特徴量数は実データに依存します。特徴量が多い場合や、意味のある特徴量が全体の中で少ない場合は推奨値よりも大きめの値を設定したほうが良い結果が得られる傾向がありますので、グリッドサーチで決定することが一般的です。グリッドサーチとは、最適なモデルとなる2つのパラメータの組合せを選ぶための処理です。
ランダムフォレストによる分類
▼サンプルスクリプト
# 環境情報
# Oracle Distribution of R version 3.2.0 (--) -- "Full of Ingredients"
# Oracle Linux Server release 6.6(2.6.32-504.16.2.el6.x86_64)
# Intel(R) Core(TM) i5-3320M CPU @ 2.60GHz
# 作業ディレクトリの指定
setwd( "working_dir" )
# 必要に応じて、パッケージをインストール
install.packages( "randomForest" )
# ライブラリの読み込み
library( randomForest )
# データの読み込み
# 事前にデー タセットをダウンロードして、zipファイルを展開
data <- "Sensorless_drive_diagnosis.txt"
drive <- read.table( data )
head( drive )
# 棒グラフで表示
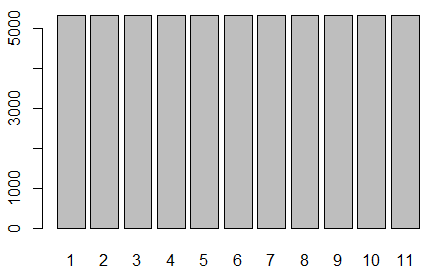
barplot( table( drive$V49 ))
▼実行結果例
1~11まで分類されたデータが存在する事が確認できます。
# モデル作成のために、トレーニング用データセットを生成する
# 元データの10%をトレーニングデータとしてサンプリング抽出
set.seed( 100 )
smpl <- sample( nrow( drive ), 0.1 * nrow( drive ))
train <- drive[smpl, ]
# 残りをテストデータ用データセットとする
test <- drive[-smpl, ]
# データセットを特徴量とラベルに分割する
features <- train[1:48]
labels <- train[49]
# ラベルをファクターに変換する
labels <- as.factor( labels[[1]] )
# モデルを作成する
modelDrive <- randomForest( x=features, y=labels, importance=T, proximity=T )
# 説明変数の重要度を表示する
print( importance( modelDrive ))
# 説明変数(分類に寄与した変数)の重要度をプロット
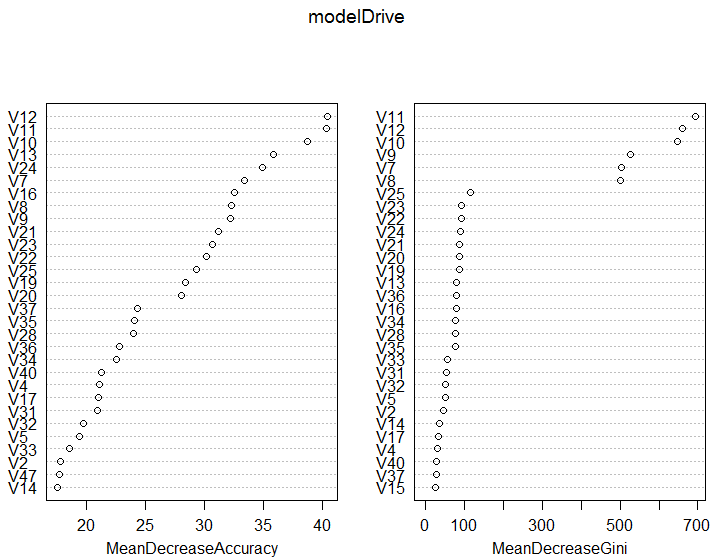
varImpPlot( modelDrive )
▼実行結果例
グラフから、V11のセンサーデータが寄与していることが分かります
# 個体間の類似度を多次元尺度法で視覚化
MDSplot( modelDrive, drive$V49 )
# 学習の収束状況をプロットする
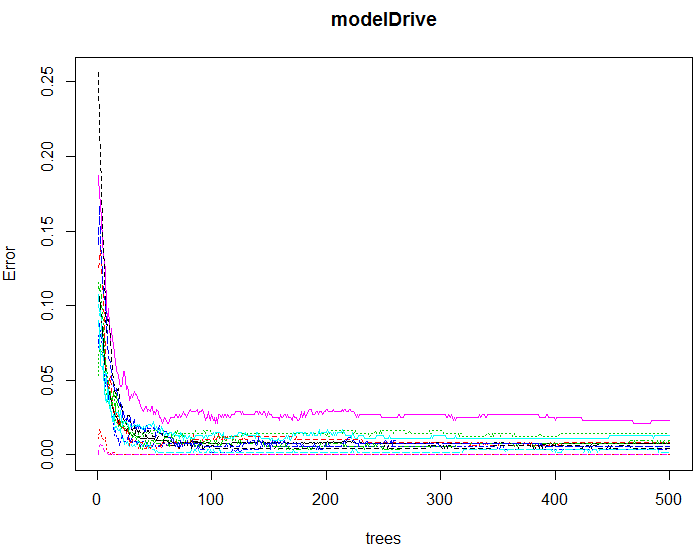
plot( modelDrive )
▼実行結果例
グラフから、300以下あたりで収束していることが分かります
グリッドサーチを行う
rfTuning <- tuneRF( x = features,y = labels, stepFactor = 2, improve = 0.05, trace = TRUE, plot = TRUE, doBest = TRUE )
▼実行結果例
実行結果から、mtry = 3 が最適であることが分かります
mtry = 6 OOB error = 1.08%
Searching left ...
mtry = 3 OOB error = 0.82%
0.2380952 0.05
mtry = 2 OOB error = 1.49%
-0.8125 0.05
Searching right ...
mtry = 12 OOB error = 1.68%
-1.041667 0.05
木の数と特徴量の数を変えて再実行する
modelDrive <- randomForest( x = features, y = labels, mtry = 3, ntree = 300, importance = T )
# テストデータにモデルを適用する
prdct <- predict( modelDrive, newdata = test )
▼実行結果例
table( prdct, test$V49 )
pred 1 2 3 4 5 6 7 8 9 10 11
1 4776 0 0 0 0 2 0 0 2 0 0
2 0 4740 0 0 0 0 0 0 16 33 0
3 0 1 4776 0 10 0 0 0 1 0 0
4 0 0 0 4805 7 0 0 19 0 0 0
5 0 0 7 2 4709 0 0 8 0 0 0
6 16 0 0 0 0 4790 0 0 5 0 0
7 0 0 0 5 1 0 4781 0 0 0 0
8 0 0 0 0 22 0 0 4758 5 0 0
9 0 2 0 0 0 5 0 0 4729 0 0
10 0 32 0 0 0 0 0 0 4 4786 0
11 0 5 0 0 1 1 0 1 0 2 4794
分類の正確さの確認
correctAns <- 0
for ( i in 1:nrow( table( prdct, test$V49 )))
correctAns <- correctAns + table(prdct, test$V49)[i,i]
correctAns / nrow( test )
▼実行結果例
99.5パーセントの精度を達成しました。
ちなみに、再実行前のモデルの場合、[1] 0.9915684でした。
[1] 0.9950246
注釈
注1:UCI Machine Learning Repository データセット
Lichman, M. (2013). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml].
Irvine, CA: University of California, School of Information and Computer Science.
注2:ブートストラップ法とは?
統計学における再標本化法に分類される、測定値から求められる経験分布を用いた統計的推論手法のこと。ブートストラップ法の利点は解析的な手法と比べて非常に単純である点。一方、欠点としては、漸近的に一致する場合には有限標本が保証されず、楽観的になる傾向がある。