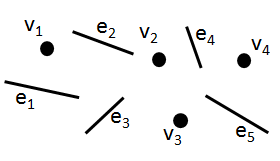位相。
英語ではトポロジーという。一般には位相よりもトポロジーのほうが耳に馴染みがあるかもしれない。数学以外の分野でも、ネットワークのつながり方のことを「ネットワークトポロジー」と言ったりする。
トポロジーというと、コーヒーカップとドーナッツを同じもの(同相)として扱う幾何学という例えがよく出てくる。これだけでは全く意味がわからないし、そんなグニャグニャした捉えどころのないものをどうやって数学的対象として取り出すのか想像もつかない。想像はつかないけれど、しかしなんだか魅力的である。ワクワクさせるものがある。
そうして、集合・位相の本を手に取り、打ちのめされるのである。
な ん だ こ れ は ? さ っ ぱ り 意 味 が わ か ら な い !
のっけから位相空間の定義がサッパリ理解できなかった。一体どうしてこれで位相なるものが定義できたことになるのか…。
理解が一歩進んだきっかけは、一つの具体例を思いついたことだった。位相空間の全容を理解したとは到底言える状態ではないけれど、開集合族によって位相、つまり「空間が連続的につながっている感じ」を表現することができる点については、ある程度理解できたと思う。その具体例とは、下図のようなシンプルなグラフ構造である。
私のような数学素人にとっては位相空間の定義は抽象的すぎてなかなかイメージを掴むことが出来ないため、このような具体的にイメージできる例を思い浮かべることが必要だった。もちろん実数体Rやユークリッド空間 $R^n$ も非常に重要な具体例の一つではあるけれど、ユークリッド空間では距離を具体的に測ることが出来てしまうため距離を捨象した空間を考える必要性が分かりにくい。またユークリッド空間は連続濃度の集合であるから極限の概念も内包してしまうため、位相というシンプルなアイディアを掴むための最初の題材としてはややハードルが高いのではないかと思う。
位相空間の定義
手元に「集合・位相入門(松坂和夫著)」がある。ここから位相空間の定義を引用しよう。
S を1つの空でない集合とする。Sの部分集合系(すなわち$\mathfrak{P}(S)$ の部分集合)$\mathfrak{O}$ が次の3つの条件を満たすとき、$\mathfrak{O}$はSに1つの位相構造を定める、あるいは簡単に、$\mathfrak{O}$はSにおける1つの位相であるという。
- $S\in\mathfrak{O}$ および $\emptyset\in\mathfrak{O}$
- $O_1\in\mathfrak{O}, O_2\in\mathfrak{O}$ ならば $O_1\cap O_2\in\mathfrak{O} $
- $(O_{\lambda})_{\lambda\in\Lambda}$ を $\mathfrak{O}$ の元から成る任意の集合族とすれば、
\bigcup_{\lambda\in\Lambda}O_{\lambda}\in\mathfrak{O}
私は最初、ユークリッド空間やらドーナツやらコーヒーカップやらにこの定義を当てはめてみて意味を理解しようと四苦八苦した。しかし、「ユークリッド空間の開集合が上記の性質を満たす」ことは理解できるものの、逆に「集合に上記定義の部分集合系を導入することで位相(=連続的につながっている感じ)を定義できる」ことがサッパリ理解できなかった。
# グラフ構造と位相
## 注(2016-03-01 追記)
本記事には、重大な誤り、あるいは大変な混乱を招く表記が含まれています。
「グラフ構造」という言葉を出しているにもかかわらず、本記事で「エッジ」と呼んでいるものはグラフ理論のエッジに対応していません。本記事での「エッジ」とグラフ理論での「エッジ」は無関係です。そのため大変混乱させる内容となってしまいました。大変お恥ずかしい限りです。
言い訳になりますが、私は3D CAD/CGの分野でソフトウェア開発に携わっておりまして、CAD等で使用されるデータ構造と数学の位相空間を結びつけてみたいというのが元々の動機でした。CADの世界で「エッジ」といえば、それは物体形状の稜線のことを指します(例えば立方体の12本の稜線のこと)。CADでは内部のデータ表現において、物体形状の頂点、稜線、面が互いにリンクしあう構造(つまりグラフ構造)を作ります。本記事の最後にある「三角形メッシュ」の例(図)がそれに相当します。そのことばかりが念頭にありましたので、CADの文脈の延長で気軽に「エッジ」という言葉を使ってしまい、それがグラフ理論の文脈でのエッジとコンフリクトしていることに全く気づいていませんでした。
グラフ理論の文脈で考えれば、CADの頂点・稜線・面はいずれも「節点」に相当するものかと思います。従って、本記事で出てくる「エッジ」という言葉は、グラフ理論の文脈では節点に相当するものだと読み替えて頂ますようお願いします。こんな混乱を招く表記をしてしまった時点でもうこの記事に価値はないような気もしますが(冷汗)、残しておきます。
(注ここまで)
~~グラフは、頂点とエッジの集まりで構成されている。~~ 本記事では、「頂点」と「エッジ」という2種類の節点からなるグラフを考える。頂点の集合を$V$、エッジの集合を$E$と置き、グラフの節点集合$S$を$V$と$E$の和集合として表すことにする。
```math
V = \{v_1, v_2, ..., v_n\} \\
E = \{e_1, e_2, ..., e_{n+1}\} \\
S = V \cup E
※ 上の注にも書きましたように、$E$はグラフ理論でのエッジとは異なるものを意図していて、節点の一部です。節点の集合$S$を、$V$と$E$の2つの集合にグループ分けした状態を意図しています。(2016-03-01追記)
しかしこれだけでは、頂点とエッジの「つながり」、すなわち位相が表現されていない。単に頂点とエッジの集まりに過ぎないので、この時点ではこれらはバラバラで繋がっていない。
ここに位相を導入して、頂点とエッジの「つながり」を定義しよう。つまりSの部分集合系 $\mathfrak{O}$ (開集合族!)を定義するのだ。
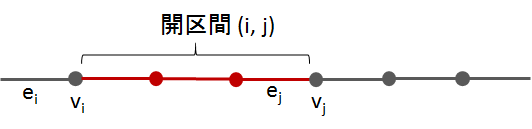
このグラフ上の「開区間」を次のように定義する。
(i, j) = \{v_k|i < k < j\} \cup \{e_k|i < k \leq j\}
図からも分かるように、「区間」の両端がエッジとなっているものを「開区間」と定めたのである。開集合はこうして定義された開区間の和集合として定義する(連結されていない飛び石の開区間の集まりも開集合であると定義する)。
こうして定義された開集合系 $\mathfrak{O}$ によって集合Sに位相が導入され、その前はバラバラの要素の集まりに過ぎなかったものが、きちんと接続関係をもつグラフとして構成されることになる。
※ グラフ構造としては、2つのグループ$V$と$E$に分けられた節点が互い違いに並んだ直線状のグラフになっています。繰り返しになりますが、$e_i$はグラフ理論におけるエッジとは違うものです。(2016-03-01追記)
- この開集合系 $\mathfrak{O}$ が上記の位相の定義を満たしていることを確認しよう。念のため注意しておくと、この開集合系は有限集合であるので、3の条件は有限個の和集合を考えれば十分である。
- ポイントは、バラバラでつながっていなかった頂点とエッジの集合が、開集合系 $\mathfrak{O}$ を与えられることによって一列に連結されたグラフ構造になるということである。いわば $S=V\cup E$ が部品セットであり、これを組立指示書 $\mathfrak{O}$ に従って組み立てると一列のグラフ構造が組み上がるということである。
…のだが、これでもやはりイメージしにくいかもしれない。次で説明する「近傍」の概念を考えたほうが、よりグラフとしての構造がはっきりと見えてくるように思う。
基本近傍系
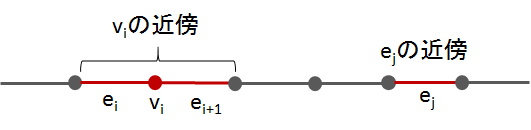
Sの各要素ごとにその近傍(基本近傍)を考えよう。その要素を含む開集合のうち最小のものを考えれば良い。つまりエッジ $e_i$ の近傍は $e_i$ 自身、頂点 $v_i$ の近傍は隣接する2つのエッジを含む最小の開区間 { $v_i, e_i, e_{i+1}$ } が基本近傍となる。
\begin{align}
N(e_i) &= \{e_i\} \\
N(v_i) &= \{v_i, e_i, e_{i+1}\}
\end{align}
これを見れば、頂点に隣接するエッジを近傍として辿ることができることが一目瞭然である。例えば隣接関係を順にたどってグラフを端から端までスキャンするような操作が可能であることが分かるだろう。
その他のグラフの例
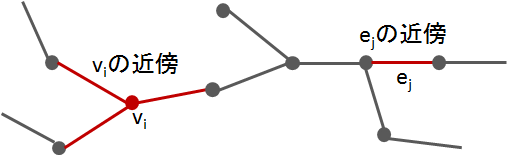
枝分かれのあるグラフ
枝分かれがあるグラフの場合も、下図のように近傍を定めれば位相を定義できる。
三角形メッシュ
3D CG などで使われている三角形メッシュは、下図のように近傍を定めることで位相を定義できる。三角系メッシュの場合は頂点とエッジに加えて面(三角形)も要素に加わっている。
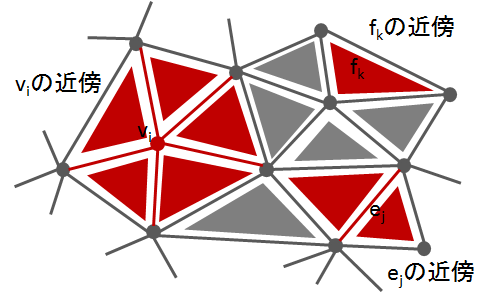
やや余談であるが、三角形メッシュに対する幾何演算を行う際にも実際にこういった位相構造は重要な役割を果たす。ある頂点やエッジに隣接する要素を取得することは、演算中でごく普通に求められるからである。三角形メッシュの位相構造は「ハーフエッジ構造」と呼ばれるデータ構造で保持するのが最も一般的である。私は三角形メッシュを含む3Dデータの幾何演算プログラムを生業としているので、データ構造としての位相構造については昔から知っていたものの、純粋な数学の位相空間との対応が取れていなかった。今回この2つを結びつけることが出来て非常にすっきりした気分を味わうことが出来た。
むすび
- 「数学ガール」に「例示は理解の試金石」という名言があった。位相空間の一つの例示としてこういったグラフ構造を考えたことで、理解が一つ深まった(というよりも親近感が増した?)ように私は感じている。
- ここで示した例は有限集合の位相の例にすぎない。なのでハウスドルフ空間とかコンパクト性とかはこの例で捉えることは出来ないと思う(←よく分かってない)。もしかするとグラフのどんどん細分化して頂点数が無限大になるような極限を考えれば良いのかもしれないが、私の理解の範囲を超えている。
- グラフ構造のうえで連続写像の面白い例が作れないかちょっとだけ考えてみたが、すぐには思いつかなかった。どなたか面白い例があれば教えてほしい。
- 三角形メッシュの例などはホモロジー論を想起させる。三角形メッシュは単体複体の一種だ。しかし私は、ホモロジー論は以前に読みかじったことがあるものの、理解には遠く及ばず関連を説明できる能力はない。鎖(chain)だとか輪体、境界輪体といったキーワードがあったような…うーん、忘れてしまった(^^; またいつか勉強しよう。