MetaTrader5(MT5)に組み込まれているテクニカル指標にDEMA, TEMAというのがあります。それぞれ Double Exponential Moving Average、Triple Exponential Moving Average の略で、2重指数移動平均、3重指数移動平均と訳されます。
この記事では、EMA、DEMA、TEMAの違いを調べてみます。
EMA
EMAの基本的な説明は以下にあります。
IIRフィルタ型の移動平均をpandasとscipyで比較してみた
計算式は
$$y(n)=\alpha x(n)+(1-\alpha)y(n-1)$$
と表され、他の移動平均と同じように期間$period$をパラメータとすると、$\alpha=2/(period+1)$となります。
DEMA
DEMAはDouble EMAの略ですが、単にEMAを2回かけることではありません。EMAを2回かけても単に平滑化が進むだけで、あまり特徴のある特性は得られません。
上のEMAの式を
$$y(n)=EMA[x(n)]$$
とすると、DEMAの計算式は
$$y(n)=2EMA[x(n)]-EMA[EMA[x(n)]]$$
と書けます。2重のEMAも使いますが、EMAも使って計算します。この式の導出原理はこちらに書いてあります。
TEMA
TEMAの計算式は
$$y(n)=3EMA[x(n)]-3EMA[EMA[x(n)]]+EMA[EMA[EMA[x(n)]]]$$
と書け、3重EMA、2重EMA、EMAを使って計算します。この式の導出原理はこちらです。
EMA, DEMA, TEMAの違い
処理例による違い
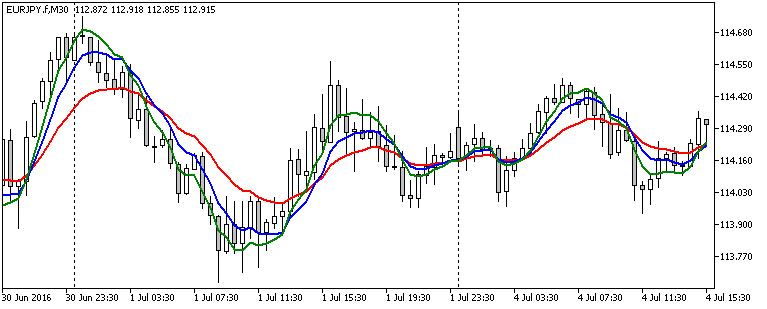
EMA, DEMA, TEMAをFXのチャートに適用させた例を示します。
これはMT5のチャートに表示させたもので、赤がEMA、青がDMA、緑がTEMAとなっています。期間はすべて同じく$period=14$としています。
これを見ると、EMAに比べて、DEMA、TEMAと価格への追従性が高くなっていることがわかります。つまり移動平均でありがちな遅延が少なくなっています。ただし、ノイズは増えているような気がします。
周波数特性による違い
上の処理例の違いは、周波数特性の違いで説明できます。
IIRフィルタ型の移動平均をpandasとscipyで比較してみた
によると、EMAのシステム関数は次のように書けます。
$$H_{EMA}(z)=\frac{\alpha}{1-(1-\alpha)z^{-1}}$$
これを使うと、DEMA、TEMAのシステム関数はそれぞれ次のようになります。
$$H_{DEMA}=2H_{EMA}(z)-H_{EMA}(z)^2$$
$$H_{TEMA}=3H_{EMA}(z)-3H_{EMA}(z)^2+H_{EMA}(z)^3$$
これに$H_{EMA}(z)$を代入して通分すると、次のようになります。
$$H_{DEMA}(z)=\frac{b_0+b_1z^{-1}}{a_0+a_1z^{-1}+a_2z^{-2}}$$
ただし、$b_0 = \alpha(2-\alpha)$, $b_1 = 2\alpha(\alpha-1)$, $a_0=1$, $a_1 = 2(\alpha-1)$, $a_2 = (1-\alpha)^2$
$$H_{TEMA}(z)=\frac{b_0+b_1z^{-1}+b_2z^{-2}}{a_0+a_1z^{-1}+a_2z^{-2}+a_3z^{-3}}$$
ただし、$b_0 = 3\alpha(1-\alpha)+\alpha^3$, $b_1 = 3\alpha(\alpha-2)(1-\alpha)$, $b_2 = 3\alpha(1-\alpha)^2$, $a_0=1$, $a_1 = 3(\alpha-1)$, $a_2 = 3(1-\alpha)^2$, $a_3 = (\alpha-1)^3$
このように変形しておくと、Pythonのscipyにある分子多項式と分母多項式の係数を引数として周波数特性を計算する関数freqz, group_delayが使えます。
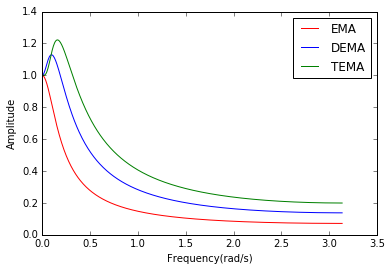
振幅特性
次のようなコードで各EMAの振幅特性を求めてみます。
%matplotlib inline
import numpy as np
import scipy.signal as sp
import matplotlib.pyplot as plt
period = 14 #期間
alpha = 2/(period+1)
# EMA
a = [1, alpha-1]
b = alpha
w, h = sp.freqz(b, a)
# DEMA
a_d = [1, 2*(alpha-1), (1-alpha)**2]
b_d = [alpha*(2-alpha), 2*alpha*(alpha-1)]
w, h_d = sp.freqz(b_d, a_d)
# TEMA
a_t = [1, 3*(alpha-1), 3*(1-alpha)**2, (alpha-1)**3]
b_t = [3*alpha*(1-alpha)+alpha**3, 3*alpha*(alpha-2)*(1-alpha), 3*alpha*(1-alpha)**2]
w, h_t = sp.freqz(b_t, a_t)
plt.xlabel('Frequency(rad/s)')
plt.ylabel('Amplitude')
plt.plot(w, abs(h), 'r', label='EMA')
plt.plot(w, abs(h_d), 'b', label='DEMA')
plt.plot(w, abs(h_t), 'g', label='TEMA')
plt.legend(loc="best")
基本的に移動平均は低い周波数を通すローパスフィルタの特性を示しますが、EMAに比べて、DEMA、TEMAは通過する帯域がちょっと広がっています。その関係で高周波の信号もある程度残っています。そのため、DEMA、TEMAは、EMAに比べて多少ノイズが残っていたわけです。
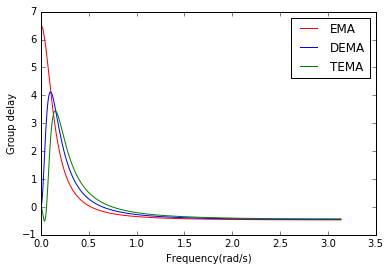
群遅延特性
次に周波数特性のなかでも、位相特性を微分した群遅延特性を求めてみます。
# 群遅延特性
w, gd = sp.group_delay((b, a))
w, gd_d = sp.group_delay((b_d, a_d))
w, gd_t = sp.group_delay((b_t, a_t))
plt.xlabel('Frequency(rad/s)')
plt.ylabel('Group delay')
plt.plot(w, gd, 'r', label='EMA')
plt.plot(w, gd_d, 'b', label='DEMA')
plt.plot(w, gd_t, 'g', label='TEMA')
plt.legend(loc="best")
群遅延特性は、その周波数における信号の遅延を表します。これを見ると、EMAは低周波における遅延が大きいのに対して、DEMA、TEMAと遅延が小さくなっています。入力の変化に対する追従性が高いのは、この群遅延特性からも説明できるのです。