Octaveを使う

はじめに

Octaveの使い方を記載します。
Octaveは数値計算用の高水準言語、開発環境です。
MATLABと互換性があります。使用したバージョンは4.0です。

簡単な導入

コメント

#以降はコメントになります。
複数行のコメントは#{ #} or %{ %}で囲みます。

# コメントです。
#{
複数行の
コメントです。
#}
%{
こちらの形式でも
OKです。
%}

電卓

コマンドラインに計算式を入力すると関数電卓として利用できます。
結果は"ans = "と表示されます。ansは最新の計算結果が格納される変数です。

# 四則演算
>> 1+2
ans =  3
>> 1-2
ans = -1
>> 1/2
ans =  0.50000
>> 2*3
ans =  6
# べき乗 2の3乗
>> 2**3
ans =  8
# 平方根
>> 2^(1/2)
ans =  1.4142

定数

円周率や自然対数の底は定義済みの定数として利用できます。

# 円周率
>> pi
ans =  3.1416
# 自然対数の底
>> e
ans =  2.7183

変数

文字列に対して代入することにより変数を定義できます。

>> x = 10
x =  10
>> y = 20
y =  20
>> x + y
ans =  30
>> z = x + y
z =  30

行の最後にセミコロン";"を入力すると結果を画面に表示しません。
計算の途中結果を画面に表示したくない場合などに便利です。

>> z;
>> z
Z = 30

定義済みの変数はwhosコマンドで確認できます。

>> whos
Variables in the current scope:

   Attr Name        Size                     Bytes  Class
   ==== ====        ====                     =====  =====
        ans         1x1                          8  double
        x           1x1                          8  double
        y           1x1                          8  double
        z           1x1                          8  double

Total is 4 elements using 32 bytes

変数の削除はclearコマンドで行います。

>> clear
>> whos

ベクトル・行列

Octaveの基本データ構造はベクトル・行列です。

ベクトルは数字の並びを"[]"で囲んで定義します。

>> v1 = [1, 2, 3]
v1 =

   1   2   3

>> v2 = [3, 4, 5]
v2 =

   3   4   5

>> v1 + v2
ans =

   4   6   8

>> v1 - v2
ans =

  -2  -2  -2

# 行と列の入替え
>> v1
v1 =

   1   2   3

>> v1'
ans =

   1
   2
   3

# 内積
>> v1*v2'
ans =  26

# 外積
>> cross(v1,v2)
ans =

  -2   4  -2

行列も同じように定義します。
複数行を区切るための記号";"を使います。

>> m1 = [1, 2, 3;4, 5, 6]
m1 =

   1   2   3
   4   5   6

>> m2 = [7, 8, 9; 10, 11, 12]
m2 =

    7    8    9
   10   11   12

>> m1 + m2
ans =

    8   10   12
   14   16   18

>> m1 - m2
ans =

  -6  -6  -6
  -6  -6  -6

# 行列の積
>> m1 * m2'
ans =

    50    68
   122   167

>> m3 = [1, 2;3, 4]
m3 =

   1   2
   3   4

# 逆行列
>> inv(m3)
ans =

  -2.00000   1.00000
   1.50000  -0.50000

# 行列式
>> det(m3)
ans = -2

# 固有値固有ベクトル
>> [v, lambda] = eig(m3)
v =

  -0.82456  -0.41597
   0.56577  -0.90938

lambda =

Diagonal Matrix

  -0.37228         0
         0   5.37228

データ型

データ型には次のものがあります。

• 実数
• 複素数
• 文字列
• struct

複素数は $x + yi$の形式で指定します。
文字列は文字の配列として扱います。
structは "value.member" の形式で扱います。 "."でメンバを示します。

# 複素数 虚数単位はi,I,j,JどれでもOK
>> c = 1 + 2i;

# 文字列 要素が文字のベクトルになる
>> s = "abcd";
# ()で参照
>> s(2)
ans = b

# structは name.member の形式で定義
>> st.name = "name";
>> st.value = 10;
>> st
st =

  scalar structure containing the fields:

    name = name
    value =  10

配列

スカラーは0次元配列です。ベクトルは1次元配列です。
行列は2次元配列です。3次元以上の配列も扱えます。

# スカラー
>> s = 10.0;

# ベクトル
# value = [value1, value2, ..., valuen]の形式で定義します。
# value(index)の形式で参照します。indexは1はじまりです。
>> v = [1,2,3]
v =

   1   2   3

>> v(2)
ans =  2

# 文字列はベクトルです
>> str = "abcd"
str = abcd
>> str(4)
ans = d

# 行列
# value = [r1c1, r1c2, ..., ; r2c1, r2c2, ...; ...]の形式で定義します。
# ;で行を区切ります。
# value(index1, index2)の形式で参照します。
>> m = [1,2,3;4,5,6]
m =

   1   2   3
   4   5   6

>> m(2,2)
ans =  5

# 3次元配列 = 複数の行列
# ランダムな値を要素とする行列を2つ作成します
# value(index1, index2, index3)の形式で参照します。index1/2/3は1はじまりです。
>> m3 = rand(2,3,2)
m3 =

ans(:,:,1) =

   0.415610   0.570380   0.010404
   0.551898   0.824296   0.268477

ans(:,:,2) =

   0.45773   0.29442   0.66975
   0.20636   0.99460   0.81495

>> m3(1,2,2)
ans =  0.29442

データ作成

ランダムな配列

ランダム値を持つ配列を作成します。

# 4行3列の行列を作成
>> d = rand(4,3)
d =

   0.62737   0.60709   0.30020
   0.80748   0.21993   0.81477
   0.84113   0.38556   0.17542
   0.25331   0.40068   0.69829

等間隔なベクトル

開始(begin)、終了(end)、分割数(N)を指定して等間隔のベクトルを作成します。

# linspace(begin, end, N)
>> linspace(1,10,4)
ans =

    1    4    7   10

底10のlogスケールで等間隔のベクトルを作成します。

# logspace(begin, end, N)
>> logspace(1,10,4)
ans =

  1.0000e+001  1.0000e+004  1.0000e+007  1.0000e+010

rangeはbegin:delta:end or begin:endの形式で指定します。
等間隔のベクトルを作成します。deltaを省略するとdelta=1とみなします。

# begin:delta:end
>> 1:3:10
ans =

    1    4    7   10

# endを超えたものは作成されません。
>> 1:3:9
ans =

   1   4   7

# begin:end, delta=1
>> 1:3
ans =

   1   2   3

行数、列数を変更する

要素数は変更しないで行数、列数を変更します。
4行3列を3行4列にします。

>> reshape(d, 3, 4)
ans =

   0.62737   0.25331   0.38556   0.81477
   0.80748   0.60709   0.40068   0.17542
   0.84113   0.21993   0.30020   0.69829

参照

行列番号を指定した参照

indexは1はじまりです。0はじまりでないことに注意してください。

>> d(1,1)
ans =  0.62737

行 or 列 番号を指定した参照

# 第2行の参照
>> d(2,:)
ans =

   0.80748   0.21993   0.81477

# 第1列の参照
>> d(:,1)
ans =

   0.62737
   0.80748
   0.84113
   0.25331

行 or/and 列 範囲指定

[begin:end]で範囲を指定できます。

>> d([1:2],:)
ans =

   0.62737   0.60709   0.30020
   0.80748   0.21993   0.81477

時間計測

tic ~ tocの間の経過時間を計測できます。
パフォーマンス測定に便利です。

>> tic;
>> toc;
Elapsed time is 1.10506 seconds.

統計計算

行列に対して、最大値、標準偏差などの統計量を計算します。
集計対象を、全体、行別、列別に指定できます。
最大値を例に説明しますが他の統計量も同じように計算できます。

>> d = rand(3,2)
d =

   0.16740   0.13353
   0.58360   0.22804
   0.46608   0.55362

# 全体
>> max(d(:))
ans =  0.58360

# 列毎に集計
>> max(d, [], 1)
ans =

   0.58360   0.55362

# 行毎に集計
>> max(d, [], 2)
ans =

   0.16740
   0.58360
   0.55362

各種統計量

# 中央値
>> median(d(:))
ans =  0.34706
# 平均値
>> mean(d(:))
ans =  0.35538
# 標準偏差(N-1)
>> std(d(:))
ans =  0.20219
# 標準偏差(N)
>> std(d(:), 1)
ans =  0.18458
# 不偏分散(N-1)
>> var(d(:))
ans =  0.040882
# 統計量まとめて計算
# minimum, first quartile, median, third quartile,
# maximum, mean, standard deviation, skewness, kurtosis
>> statistics(d(:))
ans =

   0.133526
   0.182558
   0.347062
   0.531734
   0.583604
   0.355378
   0.202194
   0.037330
   1.197839

グラフ描画

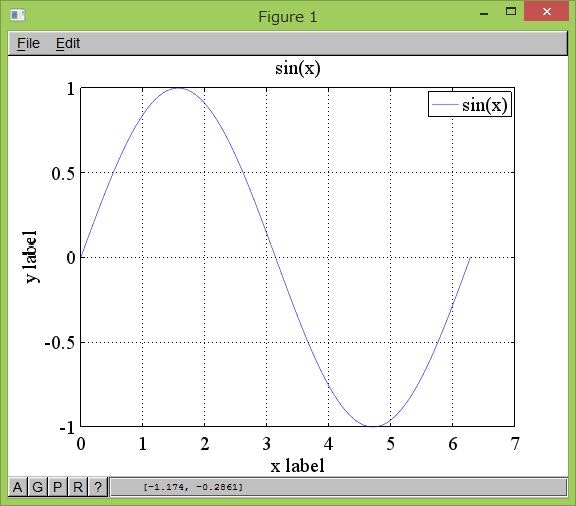
折れ線グラフ

sin関数を折れ線グラフで表示します。

# 0から2piまで100分割した値の並びを作成します。
x = linspace(0, 2*pi, 100);
# sinを計算します。yはベクトルです。
y = sin(x);
# x, yの折れ線グラフを作成します。
plot(x, y);

# フォント設定
set(gca, "fontsize", 20);
set(gca, "FontName", "Times New Roman");

# 補助線を表示します。
grid on;
# タイトルを表示します。
title("sin(x)");
# X軸ラベルを表示します。
xlabel("x label");
# Y軸ラベルを表示します。
ylabel("y label");
# 凡例を表示します。
legend("sin(x)");

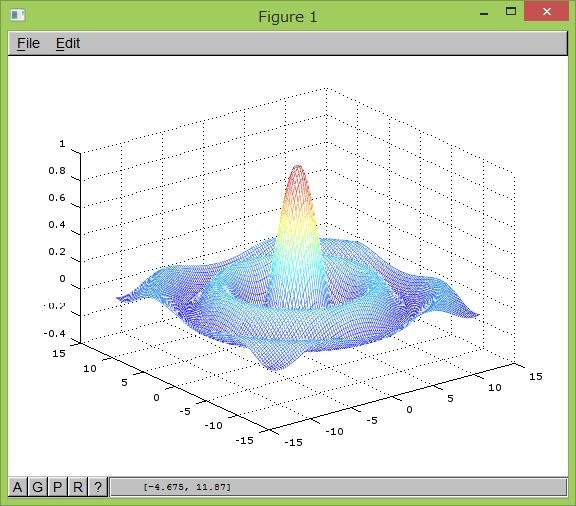
曲面グラフ描画

# x,y方向の等間隔ベクトルを作成します。
tx = ty = linspace (-pi*4,  pi*4, 101);
# x,yの等間隔メッシュを作成します。
[xx, yy] = meshgrid (tx, ty);
# 各x,y座標に対して値を計算します。これでz値が決まります。
r = sqrt (xx .^ 2 + yy .^ 2);
tz = sin (r) ./ r;
# x,y座標に対してzを描画します。3次元空間内に曲面が描画されます。
mesh (tx, ty, tz);

ファイル

ファイル保存機能を使うと、変数を保存、復元できます。
作業途中の状態を保存して、後から再開するときに便利です。

変数の保存

saveコマンドで現在の変数をファイルに保存できます。

> clear
> d = rand(4,3)
d =

   0.155614   0.225919   0.038854
   0.688431   0.614920   0.156196
   0.718452   0.669643   0.539869
   0.518844   0.361346   0.283651

> d2 = rand(4,2)
d2 =

   0.82208   0.85113
   0.36464   0.38865
   0.93129   0.58921
   0.56917   0.14110

> save d.txt

d.txtの中身です。

# Created by Octave 4.0.0,
# name: d
# type: matrix
# rows: 4
# columns: 3
 0.1556136861961896 0.2259192894373996 0.03885408396970418
 0.6884313982567527 0.614919677547173 0.1561955200532012
 0.718451508622291 0.6696427551512087 0.5398690812742165
 0.5188440254808357 0.3613462727612867 0.2836508866417567


# name: d2
# type: matrix
# rows: 4
# columns: 2
 0.8220808877083544 0.8511257313206144
 0.3646363141137096 0.3886509140540169
 0.9312928296520903 0.5892098817046786
 0.5691746305785429 0.1410993278735266

変数の復元

loadコマンドでsaveした変数を復元できます。

> clear
> whos
> load d.txt
> whos
Variables in the current scope:

   Attr Name        Size                     Bytes  Class
   ==== ====        ====                     =====  =====
        d           4x3                         96  double
        d2          4x2                         64  double

Total is 20 elements using 160 bytes

スクリプト

定型的な処理をファイルに記述しておき、繰り返し実行することができます。
拡張子は.mです。Octaveと同じパス(pwdで表示されるパス)に置きます。

test.m

1; # 関数ファイルではないことを明示する。

x = linspace(0, 4*pi, 100);
y = sin(x);
plot(x, y);
grid on;
title("sin(x)");

.mを除いたスクリプトファイル名を入力します。
スクリプトが実行されます。

> test

関数

よく利用する処理を関数ファイルに記述することができます。
拡張子は.mです。Octaveと同じパス(pwdで表示されるパス)に置きます。
ファイル名と関数名は一致させます。
先頭に記述した##で始まるコメントはhelpで表示されます。

fn.m

## usage : fn = fn(param1, param2 = 10)
function fn = fn(param1, param2 = 10)
  param1
  # param2を省略するとデフォルト値 10が使用される
  param2
  # 戻り値を設定
  fn = param1 + param2
endfunction

関数を呼び出します。

> fn(10)
param1 =  10
param2 =  10
fn =  20
ans =  20
> fn(10, 20)
param1 =  10
param2 =  20
fn =  30
ans =  30
> help fn
'fn' is a function from the file C:\Users\...\fn.m

 usage : fn = fn(param1, param2 = 10)

表示フォーマット

formatコマンドを使うことで
数字をコンソールに表示するフォーマットを変更できます。

short

最大10文字幅のフィールド内に少なくとも有効桁が5桁で数字を表示しようとする。

long

最大20文字幅のフィールド内に少なくとも有効桁が15桁で数字を表示しようとする。

bank

小数点以下2桁までの固定フォーマットで表示する。

> e
ans =  2.7183
> format short
> e
ans =  2.7183
> format long
> e
ans =  2.71828182845905
> format bank
> e
ans =  2.72

スタートアップファイル

共通設定をスタートアップファイルに記述することができます。
スタートアップファイルはOctave起動時に読込まれます。

WindowsではC:Users\UserName以下に
.octavercというファイルを作成してください。
これがスタートアップファイルになります。

次のファイルもスタートアップファイルになります。

octave-home/share/octave/site/m/startup/octaverc
octave-home/share/octave/version/m/startup/octaverc
~/.octaverc

スタートアップファイルの例を記載します。
plotの共通設定です。

.octaverc

set(0, "DefaultAxesFontsize", 20);
set(0, "DefaultAxesFontName", "Times New Roman");
set(0, "DefaultAxesXgrid", "on");
set(0, "DefaultAxesYgrid", "on");
set(0, "DefaultLineLinewidth", 2);

package

Octaveでは高度な統計処理、信号処理など特定の分野に特化した処理を、
標準ソフトウェアとは別にpackageというものに分けています。
packageを利用する方法を記載します。

インストール

Octaveコンソールで次のコマンドを実行することで全パッケージをインストールすることができます。

cd C:\octave\octave-4.0.0\src
build_packages

load

packageは利用する前にloadする必要があります。

statistics packageをloadする場合次のように記載します。

pkg load statistics;

以降、loadしたpackageの機能を利用できるようになります。