はじめに

非負値行列分解(Nonnegative Matrix Factorization;NMF)の確率的変分ベイズ法(stochastic variational Bayesian method)による解法です。
こちらの文献をまとめたものです。

Bayesian NMF

NMFは行列を非負値の行列の積に分解する、毎度おなじみのあれです。分解後の行列の各要素に事前分布を導入したものがBayesian NMFです。

X_{vd} \sim Poisson(\sum_{k=1}^{K}\beta_{vk}\theta_{kd})
\\
\beta_{vk} \sim Gamma(c_{0}/V, c_{0})
\\
\theta_{kd} \sim Gamma(a_{0}, b_{0})

同じベイズ的行列分解モデルのLDAとの対応を考えると、$\beta_{:k}$をtopicと見なせます(Bayesian NMFの$X$とLDAの$W$は転置の関係にあることは少し注意です)。

一方で$\sum_{v}\beta_{vk} \neq 1$となるところが異なります。

Stochastic variational Bayesian method

変分ベイズ法に確率的最適化を適用した学習アルゴリズムです。与えられたデータの一部を使って事後分布を更新する操作を逐次的に繰り返します。
行列データは巨大になりがちなので、一回の更新に用いるデータを絞って学習をコンパクトにできるのはとてもありがたいことですね。

イメージはこんな感じです。

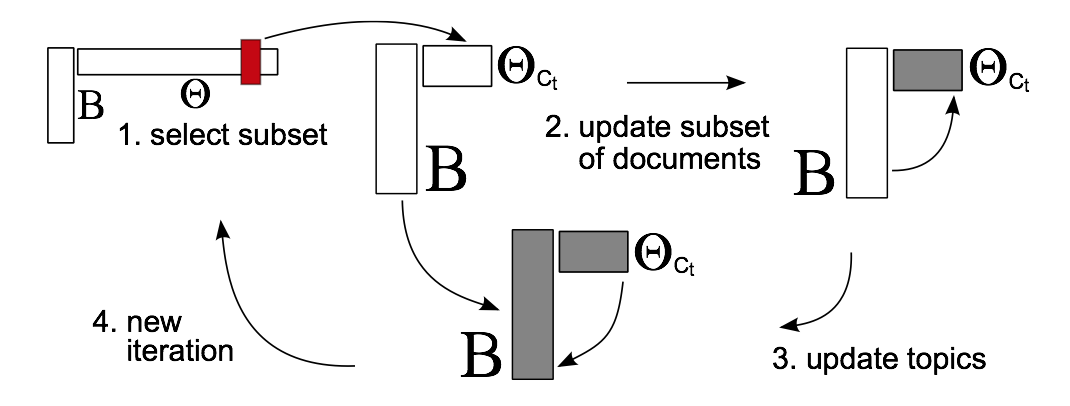
1回のイテレーションで$\Theta$を一部更新して、これを$B$全体の更新に用いています。$\Theta$はLDAで言う文書毎のトピック分布に対応することを考えると、$\Theta$を一部更新するには対応する文書だけ投入してやれば良いという訳です。

一方で$B$の更新に$\Theta$全量を使うことができなくなってしまいますが、この問題を補うのが確率的最適化というテクニックです。
発想はシンプルで、sumを含む目的関数$f(x)=\sum_{i=1}^{n}f_i(x)$を$f(x)=nE[f_i(x)]$と見なした時に、期待値の箇所を実際のサンプル$f_{i}$で近似しようという考え方です。

導出時のポイント

ポアソン分布の期待値計算において、1カ所解けない箇所があります。$E[\ln\sum_{k}\beta_{vk}\theta_{kd}]$です。この部分は次の様に下から支えてあげます。

\ln(\sum_{k=1}^{K}\beta_{vk}\theta_{kd})\geq\sum_{k=1}^{K}p_{k}^{(vd)} \ln(\beta_{vk}\theta_{kd}) - \sum_{k=1}^{K}p_{k}^{(vd)}\ln p_{k}^{(vd)}
\\
p_{k}^{(vd)} \propto \exp{(E_{q}[\ln\beta_{vk}] + E_{q}[\ln\theta_{kd}])}