概要
会社で行っている『データ解析のための統計モデリング入門』(所謂緑本)の輪読会に参加した所、
大変わかりやすい本だったものの、Macユーザには悲しい事に実装サンプルがWinBUGSだったため、
9章の一般化線形モデルのベイズ推定によるアプローチをPython + STANで実装しました。
やった事
ざっくり以下のステップを踏んでいます。
- 特定のパラメータに基いて確率分布からダミーデータを生成
- 予測モデルを設定
- ダミーデータと予測モデルから、データを生成したパラメータ(の事後分布)をMCMCで推定して答え合わせ
具体的には、とある植物の体サイズが(3.0~7.0の0.1刻みの離散値をとる)を説明変数として、
ポアソン分布に従う種子数(0以上の整数)の確率分布を推定します。
利用ツール、ライブラリ
- MCMCサンプラー: STAN(PyStan)
- 行列計算, 配列操作: NumPy
- グラフ描画: matplotlib
推定方法
MCMC
MCMC法はMarcov Chain Monte Carlo methodの略です。
日本語だとマルコフ連鎖モンテカルロ法とか言います。
マルコフ連鎖モンテカルロ法とは、モンテカルロ法を使ったマルコフ連鎖です。
…トートロジーになってしまったため、もう少し説明します。
マルコフ連鎖
ある状態が直前の状態にのみ依存するという性質の事をマルコフ性と言います。
マルコフ連鎖は、この直前の状態にのみ依存する状態が連鎖的に起こっている確率モデルです。
エンジニア的には、オートマトンの一種と考えるとわかりやすいと思います。
モンテカルロ法
モンテカルロ法は、乱数を用いた数値計算やシミュレーション一般の呼称です。
つまり、マルコフ連鎖モンテカルロ法とは乱数を使ってマルコフ連鎖を発生させる手法であり、
ここでは特に、マルコフ連鎖の持つ性質を用いて確率分布(パラメータの事後分布)を生成するアルゴリズムの事を指しています。
ベイズ推定 × MCMC
ベイズ推定のフレームワーク(事後分布∝尤度×事前分布)と、尤度に比例した確率分布をサンプリングするMCMCを組み合わせる事で、
解析的に解けないようなモデルであっても、数式で表すことさえ出来れば事後分布を推定する事が出来ます。
実装
一般化線形モデルやMCMCを詳細に解説すると大変長くなりそうなので、実装に入ります。
『データ解析のための統計モデリング入門――一般化線形モデル・階層ベイズモデル・MCMC (確率と情報の科学)』が、とにかくわかりやすいです。
訓練データの生成
体サイズは3.0 ~ 7.0、
個体毎の平均 μ = 1.5 + 0.1 * 体サイズのポアソン分布から発生させています。
def generate(n):
for i in range(n):
x = round(random.random() * 4 + 3, 1) # 3.0 ~ 7.0までの乱数
mu = math.exp(1.5 + 0.1*x)
print (x, np.random.poisson(mu))
"体サイズ" "種子数" です。
6.1 11
5.9 6
4.1 7
5.1 6
6.8 13
5.6 7
5.0 7
5.4 16
5.4 6
STAN
mcmc.stan
data {
int<lower=1> N;
vector[N] x;
int<lower=0> y[N];
}
parameters {
real beta1;
real beta2;
}
model {
for (i in 1:N) {
y[i] ~ poisson(exp(beta1 + beta2 * x[i])); // ポアソン分布×対数リンク関数
}
beta1 ~ normal(0, 1000); // 平均0,分散1000の正規分布≒無情報事前分布
beta2 ~ normal(0, 1000); // 平均0,分散1000の正規分布≒無情報事前分布
}
読み方
data
stanのプログラムに渡すデータです。
**{データ型} {変数名};**の形式で宣言します。
Pythonからここに書いた変数名を指定してデータを渡します。
parameters
こちらは、stanに記述するモデルで使用する変数です。
今回はポアソン分布の対数リンク関数の切片β1と係数β2をSTANの内部で、
無情報事前分布(を近似した分散が非常に大きい正規分布)から発生させています。
model
予測モデルです。演算子**'~'は、左項が右項の確率分布に従う、という意味合いです。
ここでは、種子数y**は、**exp(β1 + β2x)**をリンク関数(つまり対数リンク関数)とするポアソン分布に従うとしています。
Python
import numpy as np
import pystan
import matplotlib.pyplot as plt
data = np.loadtxt('./data.txt', delimiter=' ')
# Stan Interfaceに渡すデータ生成
x = data[:,0] # numpyの記法、データの1列目を切り取ってきます
y = data[:,1].astype(np.int) # ポアソン分布の目的変数なので、整数値に変換
N = data.shape[0] # データ数
stan_data = {'N': N, 'x': x, 'y': y}
fit = pystan.stan(file='./mcmc.stan',\
data=stan_data, iter=5000, chains=3, thin=10)
# iter = 各サンプリングの回数
# chain = iterで指定したサンプリングをnセット繰り返す
# thin = サンプルの間引き数
実行結果
うまく行くとこんな感じのログが出て来ます。
STAN自体はC++で実装されているので、コンパイルが走ってます。
INFO:pystan:COMPILING THE C++ CODE FOR MODEL ~ NOW.
Chain 1, Iteration: 1 / 10000 [ 0%] (Warmup)
Chain 0, Iteration: 1 / 10000 [ 0%] (Warmup)
Chain 2, Iteration: 1 / 10000 [ 0%] (Warmup)
Chain 1, Iteration: 1000 / 10000 [ 10%] (Warmup)
Chain 2, Iteration: 1000 / 10000 [ 10%] (Warmup)
Chain 0, Iteration: 1000 / 10000 [ 10%] (Warmup)
...
Chain 0, Iteration: 8000 / 10000 [ 80%] (Sampling)
Chain 2, Iteration: 8000 / 10000 [ 80%] (Sampling)
Chain 1, Iteration: 9000 / 10000 [ 90%] (Sampling)
Chain 0, Iteration: 9000 / 10000 [ 90%] (Sampling)
Chain 2, Iteration: 9000 / 10000 [ 90%] (Sampling)
Chain 1, Iteration: 10000 / 10000 [100%] (Sampling)#
...
# Elapsed Time: 9.51488 seconds (Warm-up)
# 10.7133 seconds (Sampling)
# 20.2282 seconds (Total)
#
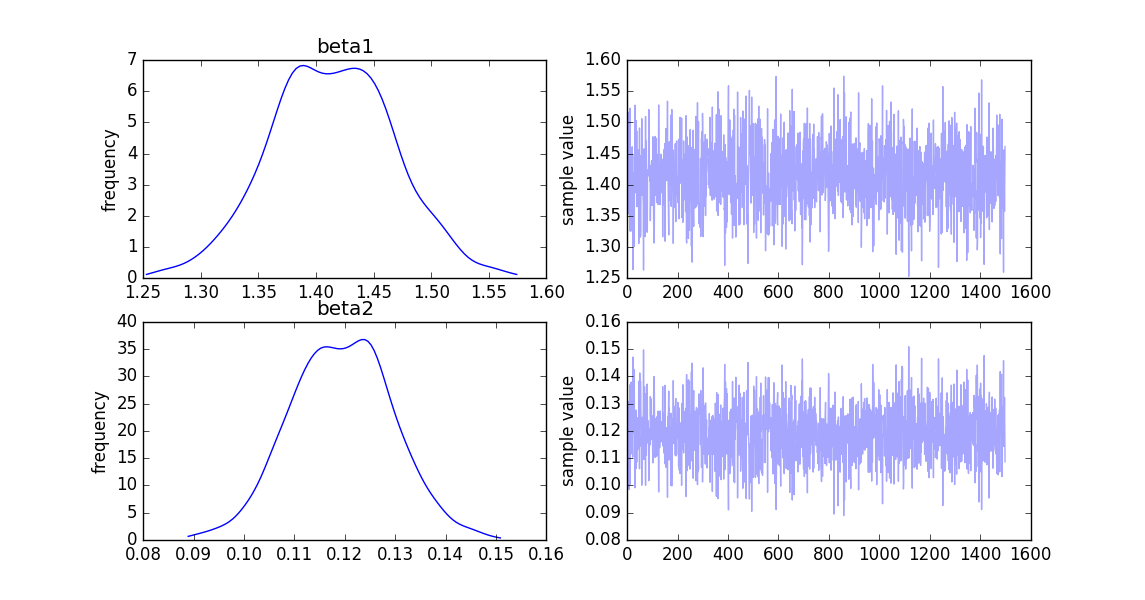
グラフ
統計値
summary
Inference for Stan model: anon_model_381b30a63720cfb3906aa9ce3e051d13.
3 chains, each with iter=10000; warmup=5000; thin=10;
post-warmup draws per chain=500, total post-warmup draws=1500.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta1 1.41 2.4e-3 0.05 1.31 1.38 1.41 1.45 1.52 481 1.0
beta2 0.12 4.6e-4 0.01 0.1 0.11 0.12 0.13 0.14 478 1.0
lp__ 7821.4 0.04 0.97 7818.8 7821.1 7821.7 7822.1 7822.4 496 1.0
Samples were drawn using NUTS(diag_e) at Tue Feb 9 23:31:02 2016.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).
fit.summary()メソッドを実行すると下記のように出力されます。
まずβ1について見ると、サンプルの平均が1.41、95%の確率で1.31~1.52の範囲にある事を示しています。(ベイズ的には信用区間と呼ぶようです。)
今回分布の山が一つだけなので代表値を平均で見てしまいますが、
β1(1.5)が1.41、β2(0.1)が0.12と大きく外れてはいない、数値を推定出来ています。
Rhat
Pythonからstanのコードをコールする際、chainパラメータでサンプリングを3回繰返しました。
MCMCによるパラメータの事後分布推定において、パラメータの初期値は適当に決めます。
モデルによっては、初期値によって推定される確率分布が異なってしまう事があるため、
サンプリングを複数回繰り返して、セット間のバラツキを数量化したRhatにより、確率分布が収束するかどうか確認します。
大体1.1以下ならOKとされているようですが、今回はbeta1, beta2共にそれ以下なので問題ないと判断できます。
参考書籍
実装紹介が中心のため、STANをコールした際のthinなど各引数の意味合いや、
なぜサンプリングの前半をWarmupに利用しているのか、
また、そもそもMCMCは手法の総称であり具体的なアルゴリズムはどうなっているのか…等々の解説を相当端折りました。
詳しく知りたい方は下記を読んで頂くと良いと思います。