モチベーション | Motivation
・お金
・機械学習の技術に触れるなど
課題 | Problem
機械学習を使ってFXの売買をするアルゴリズムを作る
問題設定 | Problem Setting
問題を単純にして解きやすくする
・2値分類問題まで落とす | set problem as 2 class classify problem
・「上がる」か「下がる」を予想 | Up or Down
・どのくらい上がったかという量は排除して考えるようにする
何が嬉しいか:
・分類の正解率=アルゴリズムの稼ぐ能力 として解釈できる | we can regard acc as trading ability
・そうしないと、正解率は高いけど期待値は低いので使えない、みたいなややこしさ
どのように2値分類問題にするか
指値(指定した値段で売る/買う)を使えばOK
・例:値幅±0.5円で勝負 | example
・・現在値118.0円でロング(上がる)予想でエントリーした場合 | forcast "Up" at 118.0 Yen
・・・先に118.5円になればアタリ | 118.5 Yen... CORRECT!
・・・先に117.5円になればハズレ | 117.5 Yen... WRONG!
この上がるか下がるかの正解率を高めることが目標になる
どのように解くか
機械学習の中でも割りと簡単といわれるナイーブベイス(Naive Bayes)をまずは使ってみる。
ナイーブベイズはスパムメールかどうかを分類するのにも応用されている。
同じ要領で為替予測においても上か下かの分類問題として適用できる。
By Using Naive Bayes which is one of machine learning alg.
ナイーブベイズの説明 | What is Naive Bayes
略:http://aidiary.hatenablog.com/entry/20100613/1276389337
式の解釈(スパムメール判定の場合): | Example of Spam Email Classify
式:P(cat|doc)=P(cat)P(doc|cat)P(doc)∝P(cat)P(doc|cat)
P( スパム|判定したいメール) =
あるメールがスパムである確率 *
判定したいメールの単語[1]がスパムメールに含まれる確率 *
判定したいメールの単語[2]がスパムメールに含まれる確率 *
...
P(非スパム|判定したいメール) =
あるメールが非スパムである確率 *
判定したいメールの単語[1]が非スパムメールに含まれる確率 *
判定したいメールの単語[2]が非スパムメールに含まれる確率 *
...
ナイーブベイズの雰囲気:
事前にわかっている確率を、後に得られた情報からどんどん更新していく感じ。
例:スパムメール
・事前にわかっている確率:
・・メールがスパムである確率=いままで受け取ったスパムメール数 ÷ いままで受け取った全メール数 = 0.4
・・メールが非スパムである確率=1-メールがスパムである確率 = 0.6
・事後に得られた情報からどんどん更新
・・このメールに「入金」という単語が含まれていたとして、
・・・「入金」という単語がスパムメールに含まれている確率は0.01
・・・「入金」という単語が非スパムメールに含まれている確率は0.001
・・・この情報を事前確率に反映
・・・・P(スパム|メール) = 0.4 * 0.01 = 0.004
・・・・P(非スパム|メール) = 0.6 * 0.001 = 0.0006
・・・・この反映によりスパムメールの確率が高まった!
・・・・・さらに他の単語も同様に掛け合わせてゆく...
スパムメール分類の流れ:
学習:教師データ(大量のスパムメールと非スパムメール) → 学習モデルの生成
適用:新しいメールが来る → 学習器で判定 → 結果{スパム/非スパム}
「学習モデルの生成」とは、どの単語がどのスパムメールで何回出たとかを記録するだけで大層なことはしていない。
為替予測での上下分類の流れ:
学習:教師データ(上が正解となる例と下が正解となる例) → 学習モデルの生成
適用:新しいメールが来る → 学習器で判定 → 結果{スパム/非スパム}
スパムメールの時は、教師データの特徴として「メールに含まれる単語」を扱ったが、為替予測の場合では、様々なものが考えられる
例:
・チャート上の情報
・・直近の足の上がり下がり
・・などなど
・チャート以外の情報
・・直近の天気
・・直近の世界中のTwitter
・・直近のニュース記事
実装
・ナイーブベイズのアルゴリズムはこちらのコードをそのまま使える
略:http://aidiary.hatenablog.com/entry/20100613/1276389337
・過去のチャートデータは「ヒストリーデータ」などでググったらでてきます
ナイーブベイズの事前確率
過去のチャートを学習する時に事前確率(上が正解となる確率、下が正解となる確率)は自動的に求まる。
例えば学習期間中ずっと下がり続けるような相場だった場合、事前確率は下が強くなる。
この事前確率の傾倒は、言い換えると、機械が「まあ、市場は概ね下がるもんだろう」と勝手に仮定しているような状態で、為替の場合はあまりよくない。
ごく自然に考えると市場は常にどちらに向かうのかわからないので、事前確率は上も下も1/2に修正した方がいい。
def score(self, doc, cat):
"""文書が与えられたときのカテゴリの事後確率の対数 log(P(cat|doc)) を求める"""
total = sum(self.catcount.values()) # 総文書数
#score = math.log(float(self.catcount[cat]) / total) # log P(cat)
score = math.log(float(1) / 2) # log P(cat)
for word in doc:
# logをとるとかけ算は足し算になる
score += math.log(self.wordProb(word, cat)) # log P(word|cat)
return score
事前確率をこのように主観的に選ぶべきか、それともデータに従って客観的態度で選ぶべきかは議論が別れるもよう(『Think Bayes』P31)
テストと評価
偶然うまくいった系(カーブフィッティング)とどう向き合うか
偶然うまくいった系
・ランダムに取引していても聖杯に見える結果をだすことがまれにある
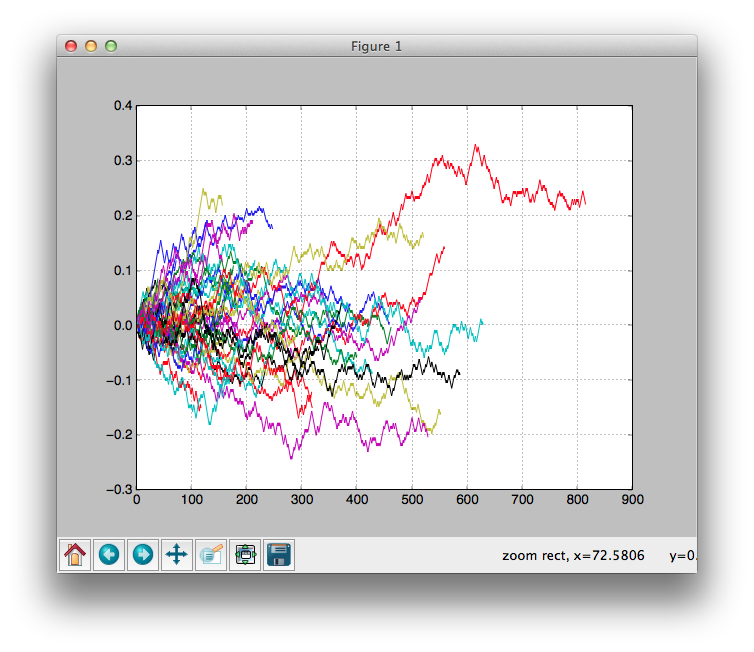
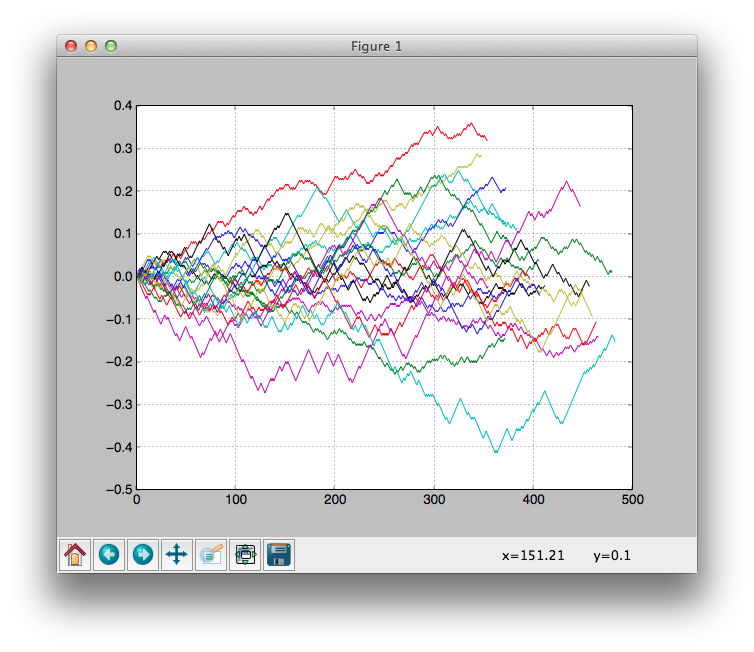
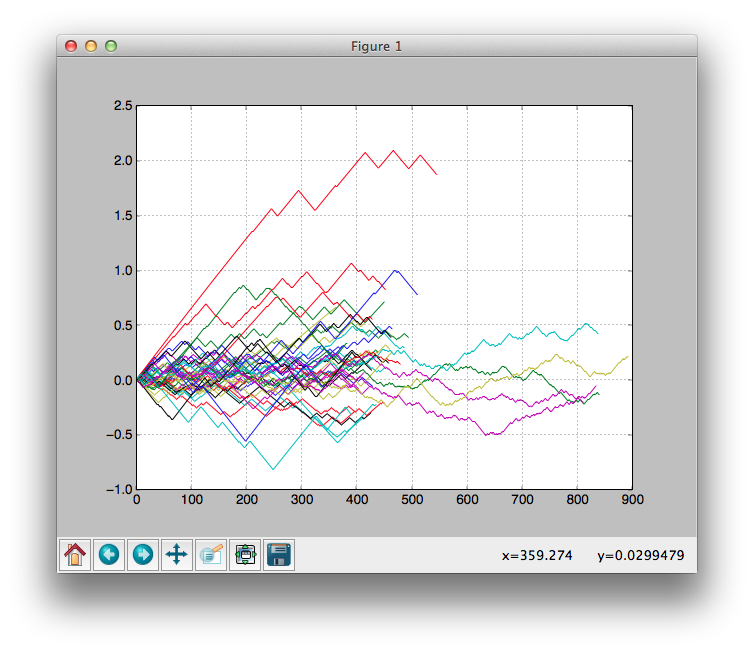
・下のグラフはランダムに取引するアルゴリズムの収益変化をプロットしたもの
・1つの実験結果だけに頼ると、グラフ上部の赤い線のように常に上昇している結果が現れた時に聖杯だと勘違いしてしまいやすい
・・聖杯だと勘違いし何日間もブラッシュアップ...という無駄骨
・・・最悪、本番投入してしまい想定外の結果を招く
・どう排除するか
・・試行回数を増やす
'''
--- TEST 1 --------------------------------------------
MONTH : 01 02 03 04 05 06 07 08 09 10 11 12 01 02 03 ...
LEARN : <--------------->
TEST : <->
--- TEST 2 --------------------------------------------
MONTH : 01 02 03 04 05 06 07 08 09 10 11 12 01 02 03 ...
LEARN : <--------------->
TEST : <->
--- TEST 3 --------------------------------------------
...
'''
のように、テストと検証の1セットを少しずつ期間をずらしながらやって、それらの結果の平均をみる
・ランダムで取引し正解率が50.0%に十分に収束するのを確認してからがスタートライン
実験結果
・データ:ドル円 1時間足 2004-2014年
・特徴量:過去5時間のヒゲの長さをクラス化したもの
・その他:尤度差が小さい時は見送っている
・正解率:0.514660470318
書くほどの精度はでなかったが、安定して51%以上がでるようになったことから、多少は学習の効果が反映されているものと思われる。
今後の課題
いろんな特徴量を試す
・有名な特徴量
・・移動平均線
・・ボリンジャーバンド
他のアルゴリズムを試す
・深層学習を試してみたい
追記 2015-09-18:
他の特徴量の内すぐに試せるものについてはいくつか試してみたら、精度が53.91まで改善した。
一番良かったときの特徴量は、現在値が移動平均(10時間平均)の下か上かというそれだけ。それと、訓練データの内10時間以内にしきい値に達しない中途半端な動きをするものは棄却した。
もっと精度あげたいという衝動でいろんな特徴の組み合わせを試したくなるが、このあたりでほどほどに切り上げる。最初は幅広くいろんな手法を試す方が効率いいとおもうので。
特徴の組み合わせは無数に存在し、人間が手動であれこれ試すのは非効率のように思う。ディープニューラルネットはローレベルなインプット情報の組み合わせから勝手に有効な特徴が浮かび上がってくるという理解で、このあたりも解決してくれる?っぽいので、そういう意味でも次はディープニューラルネットを試してみたい。