この記事は機械学習に必要な高校数学やり直しアドベントカレンダー Advent Calendar 2016の16日目の記事です。
近くにいる人から、そもそも「線形代数」の「線形」って何のこと?と訊かれたので、簡単にまとめてみます。
線形とは
線形という日本語は、知らない人から見れば確かに分かりにくいですね。
英語を調べてみると、
線形代数
linear algebra
linear algebras
です。さらにlinearを調べると、
linear
【形】
線の、線形の、線状に伸びる、直線の、直線状の、長さの
で、「直線状の(line + ar)」という意味になります。
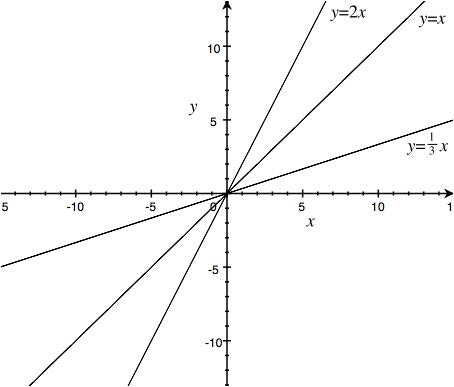
つまり、「線形」というのは変数と変数の関係が直線的ということを意味してます。これをグラフに書くと、
で表される関係ということになります。
線形の定義
線形は次の2つの特徴を持っています。
- $f(x+y)=f(x)+f(y)$
- $f(kx) = kf(x) $ ただし、$k$は実数
つまりこの2つの性質が成り立つ関係を線形と言います。例として上のグラフの$f(x)=2x$でこの性質が成り立つかどうか見てみます。
まず、1についてですが、
\begin{align}
f(x+y)
&= 2(x+y) \\
&= 2x + 2y \\
&= f(x) + f(y)
\end{align}
と成り立ちます。2については
\begin{align}
f(kx)
&= 2(kx) \\
&= k(2x) \\
&= kf(x)
\end{align}
と成り立ちます。したがって、$y = 2x$は線形だと言えます。では、$y=2x+1$は線形でしょうか? この関数で上の性質が成り立つか計算してみます。
まず、性質1から計算します。
\begin{align}
f(x+y) &= 2(x + y) +1 \\
&= 2x + 2y + 1 \\
&\neq f(x) + f(y)
\end{align}
となり、性質1が成り立ちません。したがって、$y=2x+1$は線形ではありません。こういうのは非線形と言います。
上のグラフに示したような直線の場合、原点を通る直線だけが線形であると言えます。
線形性の例
参考文献にあげた「高校数学の美しい物語」からいくつか線形性の例を挙げてみます。
例1 シグマ
\begin{equation}
\sum_{i=1}^{n} (ax_i+by_i) = a \sum_{i=1}^{n} x_i + b \sum_{i=1}^{n}y_i
\end{equation}
上の式で性質1と2の両方が成り立つことが分かります。したがって、総和は線形と言えます。
例2 ベクトルの内積
3つのベクトル$\vec{p}$、$\vec{q}$、$\vec{r}$を考えた時、
\begin{align}
\vec{p}\cdot(a\vec{q} + b\vec{r})
&= \vec{p} \cdot a\vec{q} + \vec{p}\cdot b\vec{r} \\
&= a \vec{p} \cdot \vec{r} + b \vec{p} \cdot \vec{r}
\end{align}
$\vec{p}\cdot\vec{q}$は2つのベクトルの内積なので、性質1と2の両方が成り立つので、内積も線形と言えます。
このように高校数学の範囲でも線形の関数はいろいろあります。
終わりに
普段、道具として数学(の一部)を使っているだけだと、あらためてごく基本的なことを聞かれた時、正確な定義はどうだったかなとか一瞬ためらいます。うろ覚えになってた基礎をたまには見返すのも良いんじゃないでしょうか。