Autogradという野郎が乗り込んできたのでガクブルな件

Autogradという野郎が乗り込んできました。はい、そりゃもういきなり。複雑な確率モデルや損失関数だとしても、パラメータに関する勾配をこれでもかというぐらい簡単に計算できちゃうので、機械学習の世界に大きな影響を与えそうです。現時点では、PythonとTorchでの実装が公開されているようですが、これからJuliaなど他の言語でも実装されていきそうですね。

（補足：この記事を書いたすぐ後にGoogleがTensorFlowなるものを出してきまして、そちらでも自動微分がしっかり実装されてるみたいです〜。機械学習関連のフレームワークは移り変わりが激しいですねー ^^; ）

ちなみに始まりはこんな感じでした。

ゆるいですね。

とりあえずチュートリアルやりながら、Python版チュートリアルの前半部分にテキトーな日本語訳をつけたので、ここでシェアしておきます。英語が読める方は、僕のヘンテコな日本語訳を読むより、英語の原文（Autograd tutorial）を読むことをオススメします。

以下、Python版チュートリアルの前半部分のテキトーな日本語翻訳です。

モチベーション

手元にあるデータを使って、ある確率モデルのトレーニングしてみたい場面を想像してみましょう。この場合、まずは確率モデルとそのモデルの良さ（確率モデルがどれだけデータをよく表しているか）を測るための損失関数を用意しますね。次に、このモデルと損失関数を基に、モデルのパラメータを最適化します。いわゆる学習ですね。簡単なモデルであればバッチ最適化手法を用いて一発で最適なパタメータが求められたりしますが、ニューラルネットワークのようにパラメータ数が多く複雑なモデルだと、逐次最適化手法に頼らざるを得なくなり、勾配を計算する必要がでてきます。

こうなると現時点では２つの方法が残ります。

• １つ目の方法は、紙とペンで勾配を計算し、出てきた答えをガリガリコーディングするというやり方です。
• ２つ目の方法は、Theanoのようなライブラリの構文に従って確率モデルをコーディングするというやり方です。

Autogradはこれに対し、３つ目の方法を提供します。

• ３つ目の方法は、損失関数をnumpyのような数値計算ライブラリで実装してAutogradに渡すというやり方です。

後はAutogradが自動微分（Automatic Differentiation）のリバースモード（いわゆるbackpropagation）を使って自動的に勾配を求めます。

Autogradの使い方

Autogradが提供するgrad関数に損失関数を渡すだけです。そうすると、損失関数の勾配を計算する関数が返ってきます。

ちなみにgrad関数に渡す関数はスカラ関数（返り値がfloatなどのスカラ値）である必要があります。

Autogradは、Pythonのwhileループやif文やクロージャなどの制御構文やnumpyのデータ型に対して働きかけ最終的な勾配関数を導きだすので、grad関数に渡す損失関数はPythonとnumpyを使ってかなり自由に記述できます。

簡単な例

まずautogradというパッケージをpip isntall autogradでインストールし、必要なモジュールを読み込みます。

import autograd.numpy as np # Numpy用の薄いラッパ
from autograd import grad

関数（機械学習したければ損失関数。以下、「損失関数」という言葉を使用）を定義します。sin(x)を定義する際にforループをぶん回している点に注目して下さい。（コメント欄に以下のコードの意味のざっくりとした解説を乗せておきましたので、コードがチンプンカンプンの場合はどうぞー。）

def taylor_sine(x):   # サイン関数のテイラー近似（マクローリン展開）
    ans = currterm = x
    i = 0
    while np.abs(currterm) > 0.001:
        currterm = -currterm * x**2 / ((2 * i + 3) * (2 * i + 2))
        ans = ans + currterm
        i += 1
    return ans

描画用ライブラリを読み込んで、

import matplotlib.pyplot as plt
%matplotlib inline

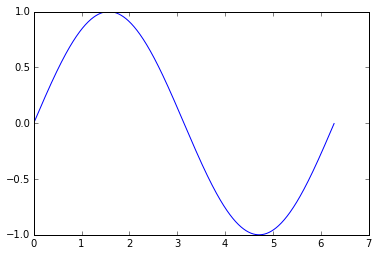
まずは損失関数自体を描画します。

# 損失関数
xs = np.arange(0, 2 * np.pi, 0.01)
ys = np.asarray([taylor_sine(x) for x in xs])
plt.plot(xs, ys);
plt.ylim([-1.0, 1.0]);

ここでおもむろに、grad関数に損失関数を渡します。すると勾配関数が帰ってくるので受け取ります。ただこれだけです。

# grad関数に損失関数を渡して、勾配関数を受け取る
grad_sine = grad(taylor_sine)

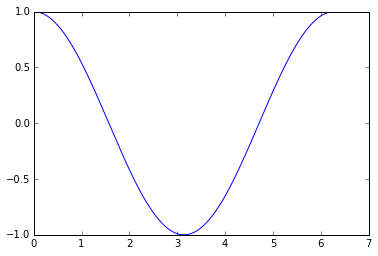
描画してみると、$\frac{d\sin(x)}{dx} = \cos(x)$がちゃんと返ってきていることがわかります。

#  パラメータの各点における勾配を計算して描画
dydxs = np.asarray([grad_sine(x) for x in xs])
plt.plot(xs, dydxs);
plt.ylim([-1.0, 1.0]);

実際の学習に用いた例：ロジスティック回帰

次に、Autogradで求めた勾配を使って、実際に学習してみます。モデルにはロジスティック回帰モデルを使ってみます。

まず先ほどと同様、autogradから必要なモジュールを読みこみ、確率モデルと損失関数を定義します。

import autograd.numpy as np
from autograd import grad

def sigmoid(x):
    return 0.5 * (np.tanh(0.5 * x) + 1) # typo in the original
    
def logistic_predictions(weights, inputs):
    # ロジスティック回帰モデルで予測されたy=1となる確率。
    # バイアス項は無し。
    return sigmoid(np.dot(inputs, weights))    

def training_loss(weights):
    # トレーニング用損失関数には負の対数尤度（negative log-likelihood）を用いる
    preds = logistic_predictions(weights, inputs)
    label_probabilities = preds * targets + (1 - preds) * (1 - targets)
    return -np.sum(np.log(label_probabilities))

次に、データセットを用意します。

# 小さなデータセットを作成
inputs = np.array([[0.52, 1.12,  0.77],
                   [0.88, -1.08, 0.15],
                   [0.52, 0.06, -1.30],
                   [0.74, -2.49, 1.39]])
targets = np.array([True, True, False, True])

ここまで来たら、おもむろにgrad関数を呼び出し、勾配関数をゲットします。

# autogradを用いて、トレーニング用損失関数のモデルパラメータに対する勾配を求める
training_gradient_fun = grad(training_loss)

勾配を計算できるので、勾配法を用いて逐次的にパラメータをアップデートしていくと、損失関数の値が下がります。

# モデルパラメータを勾配法を用いて逐次最適化

losses = []

weights = np.array([0.0, 0.0, 0.0])
loss = training_loss(weights)
losses.append(loss)
print "Initial loss:", loss

for i in xrange(100):
    weights -= training_gradient_fun(weights) * 0.01
    loss = training_loss(weights)
    losses.append(loss)

print "Trained loss:", loss    
losses = np.asarray(losses)

Initial loss: 2.77258872224
Trained loss: 1.06727067579

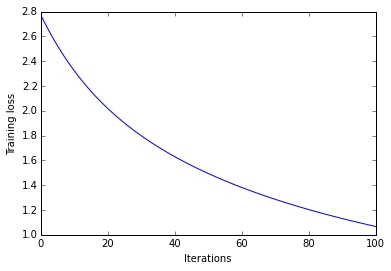
途中経過の値をプロットするとこんな感じです。しっかり学習できてますね。

plt.plot(losses)
plt.ylabel("Training loss")
plt.xlabel("Iterations")

Pythonを使うと確率モデルを簡単に記述できます。Autogradによってもたらされる最大の恩恵は、モデルの変更しても面倒な手順を踏まずにサクッと学習が始められる点です。

examplesディレクトリには以下の例を含むいろいろなサンプルコードがあります。

• Simple neural net
• Convolutional neural net
• Recurrent neural net
• Long short-term memory (LSTM)
• Neural Turing Machine
• Backpropagating through a fluid simulation
• Variational inference in Bayesian neural network
• Gaussian process regression

以上、Autogradの紹介でした。内部的にどうやってやっているのかという点については、気が向いたら書くかもですー。それでは、また〜。

リンク集

Python系実装

• Autograd for Python @ GitHub
• チュートリアル
• 用例集

Torch系実装

• Autograd for Torch @ GitHub
• チュートリアル