Competitive Programming (その2) Advent Calendar 2015の14日目の記事です。
Topcoderマラソンマッチ初心者向け、主にTopcoderで出題される探索問題に取り組むときに重要だと思っていることを書きます。
任意のマラソン系コンテストで重要なこと
まず、Topcoder MMの探索問題に限らず、マラソン系コンテストで重要なことについて。
時間で殴る
BFS、DFS、Dijkstraなど基本的なアルゴリムズを使いこなせる人(ABCのC,ARCのBぐらいが解ける人)なら、時間さえかければマラソン系コンテストで良い成績を残せると僕は思っています。
最低でも10時間ぐらいは頑張って取り組んでみてください。
よく考察をする
時間をかけていたとしても、間違った方針の実装を永遠とやっていたのでは意味がありません。実装を始める前によく考察をして、これでいけると何かしらの確信を持ってから実装に入るのをお勧めします。100%確信(数学的な根拠を見つけるなど)してから実装をしているわけではありませんが、これ以上考察するよりも実装してしまったほうが速いという段階まで持っていくのが良いと思います。僕の場合だと、最初の10時間ぐらいは考察に時間を使います。考察時にプログラムを書くこともありますが、あくまで考察のための実験です。
有名アルゴリズムに囚われない
マラソン系コンテストが終わった後に、「ビームサーチした」「焼き鈍した」というのをよく見かけます(僕もよく言いますが)。しかし、ビームサーチや焼き鈍しを使う問題であっても、実はビームサーチや焼き鈍しはそれほど重要ではありません。いえ、上位に入るには必須な場合も多いんですが、使っていれば上位に入れるかというとNoです。なんとなくビームサーチを使ってみたけど上位5割にも入れなかったという人は結構いるんじゃないかと思います。有名アルゴリズムに囚われずにその問題をよく考察してみましょう。
探索問題
ここで扱う問題はTopcoder MMでよく出題される、一人確定完全情報ゲーム、もしくは最適化問題です。一人確定完全情報ゲームは簡単にいうと、プレイヤーは一人、ランダム性はなく、盤面などの情報が全てわかるゲームのことです。コンテストとしては、その問題をプログラムに解かせて、よりハイスコアを取ろうというものです。この手の問題はほとんどの場合探索して解きます。
探索空間
探索空間は問題に応じて設計する必要があります。また、その探索空間の形を意識すべきです。よく見られる探索空間の形には、大きくわけてビームサーチ系と焼き鈍し系の2つがあります(この呼称は僕が勝手に呼んでいるだけ)。
ビームサーチ系
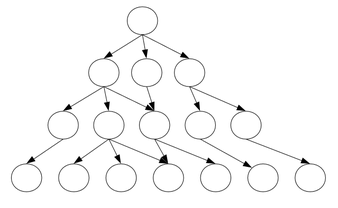
初期状態から始まるDAG(Directed Asyclic Graph)になっています。ビームサーチ探索空間になる問題のゲームは、ターン制のものが多いです。遷移は、ゲームのターンを進めることに対応することが多いです。最終的に求めたい解は、初期状態から終了状態までどういう遷移をしてきたかです。
初期状態から深さが深くなるごとに状態数が指数的に増加します。もちろん全状態を探索することは不可能なので、ビームサーチで探索すると良い場合が多いです。
焼き鈍し系
深さなどの意味合いはありません。遷移は、状態の一部を変更することに対応することが多いです。最終的に求めたい解は状態そのもので、ビームサーチ系とは違い、ほとんどの場合どういう遷移をしてきたかに依存しません。
焼き鈍し系と言っていますが、実は僕は本来の焼き鈍し法をコンテストで使ったことがありません。山登り法か局所探索をしています。使ったことがない理由は、単に僕が焼き鈍すのが下手なだけです。ただし、それでも上位1割ぐらいには入れます。
探索空間
探索の問題では、ビームサーチがどうとかの前に重要なことがあります。ビームサーチなどのメタヒューリスティクスアルゴリズムは、探索空間を良い感じに探索するアルゴリズムです。つまり、探索アルゴリズムの前に探索空間があるんです。多くのコンテストでは、探索アルゴリズムよりも探索空間を工夫することのほうが圧倒的に重要です。
状態
盤面の状態、現在のターン数など。
評価関数
状態を数値化する関数で、評価関数 = 問題のスコア + 良い特徴 - 悪い特徴という形を取ることが多いです。
評価関数は問題のスコアだけでも上位に入れるコンテストが結構あります。redcoderと競うレベルになると頑張らないとダメなことが多い印象です。
遷移
特にTopcoder MMでは超重要。遷移を問題での1ターンの行動そのままにするとダメなことが多いです。探索空間中の状態がゴミ状態だらけになり、例えばビームサーチ系探索空間でビーム幅1145141919810のビームサーチをしたとしても全く良いスコアが出ないことがあると思います(実行時間の制限上、ビーム幅は大きくても1000~100000ぐらいです。要するにこのままじゃダメってこと)。
遷移を設計する際に僕が指針としている考えは、確実に前進です。
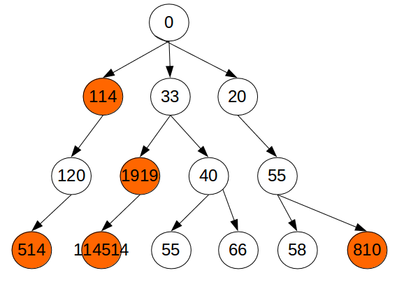
ノード内の数値はその状態の評価値を表しています。説明の図で色が付いている状態は、遷移前の状態よりも評価が良くなったことを示しています。
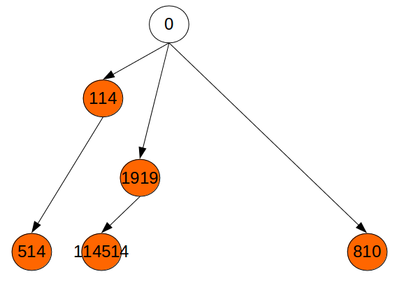
イメージとしては、上の探索空間(ゲームの行動そのまま遷移)を下の探索空間(確実に前進遷移)になるように遷移を設計すると良いです。
ほとんどの問題で、上の探索空間でビームサーチをするよりも、下の探索空間でgreedyするほうが良い結果が出ると思います。マラソン系に強い人がgreedyは強いと言うことがあります。そういった発言は、確実に前進遷移な探索空間ならgreedyでも良いスコアが出るんだ、と僕は解釈しています。
上記の説明では、ビームサーチ系探索空間を用いましたが、焼き鈍し系探索空間の場合も同様に確実前進遷移を設計すると良いです。焼き鈍し系探索空間でのgreedyな探索アルゴリズム(山登り法 or 局所探索)でも十分スコアが出ます。
TCO 2014 MM Round1 SquareRemoverを考える
問題概要
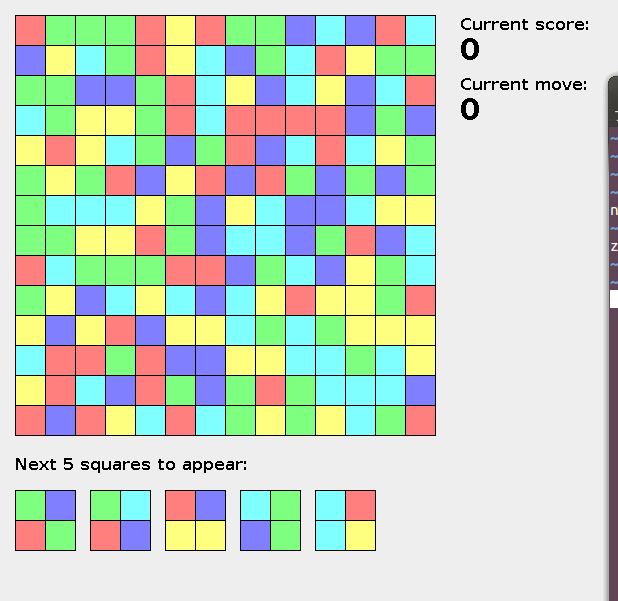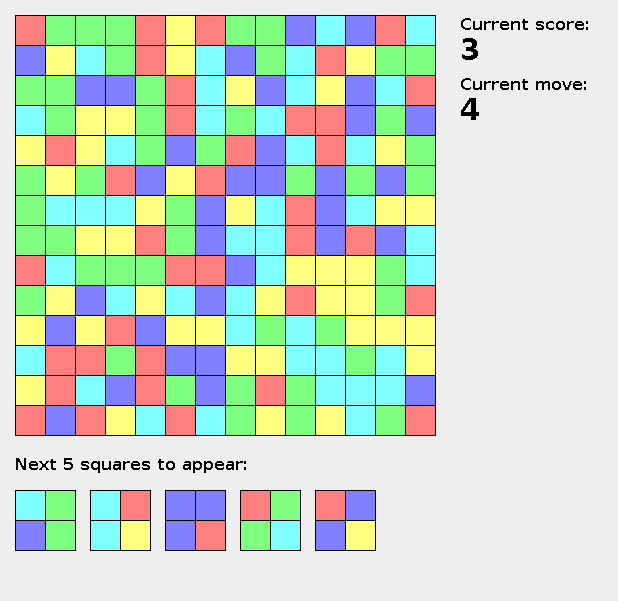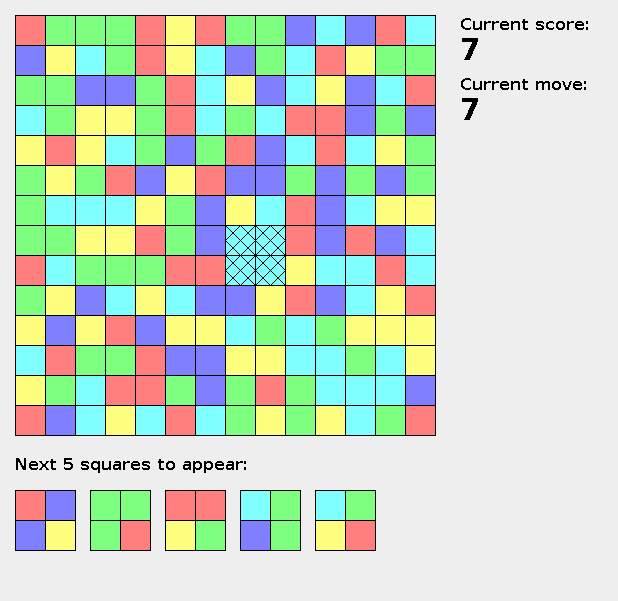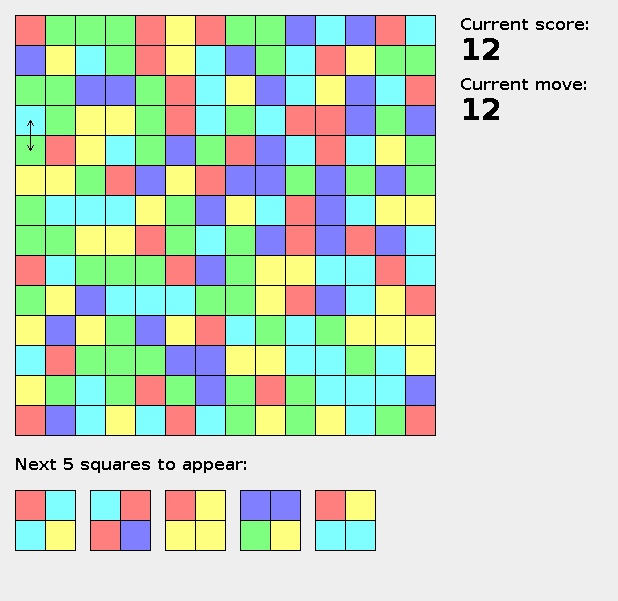
二次元の盤面が与えられ、各セルには色がある。1ターン毎に隣接するセルの色を交換することができる。辺の長さ2の正方形内セルの色が全て同じになった場合、スコアが+1され、正方形内の色がNextの先頭の色に置き換えられる。置き換えられた後に色が同じになった場合、更に置き換えが起こり、この時ターンは進行しない。色が揃った正方形が複数ある場合は、(y, x)が小さいが優先的に処理される。Nextは完全に把握できる。10000ターンあるとき、より大きいスコアを獲得せよ。
制約
盤面は正方形、辺の長さ: 8~16
1ケース内の色の種類: 4~6
探索空間
状態は盤面、 評価はゲームのスコアでも十分な結果が得られます。問題は遷移をどうするかです。ただ、この時点でビームサーチ系の探索空間であることはわかりますね(わかって)。
1ターンでの交換の仕方はO(wh)です。遷移を1ターンの交換に対応させると、ある正方形の色を揃えるのにnターンかかるとすると、その正方形の色を確実に揃えるには、ビーム幅はO((wh)^n)必要になります。ダメみたいですね。
確実に前進できる遷移を考えてみましょう。この問題は、正方形の色を同じ色に揃えるとスコアが上昇するというルールです。つまり、遷移をある正方形の色を揃えるにすると、1回の遷移で確実にスコアがプラスされることになります。いいぞ〜これ
探索木の深さを何に対応させるかを考える必要があります。何回遷移したか(何度正方形の色を揃えたか)を深さに対応 or 何ターン目かを深さに対応させる方法があります。この問題では何ターン目かに対応させると良いです。なぜなら状態に何ターン目かを持つ必要がなくなります。そうすると評価関数でターン数を考慮する必要がなくなるからです。
後、この問題では評価関数に加えるべき重要なポイントがあります。サイズ2の正方形内に同じ色が3つある場合は加点するようにすると上位1割ぐらいには入れます。
まとめ
時間で殴る
よく考察して
詰まったら確実に前進する処理を考えてみる