ずいぶん遅くなりましたが、ひとまず完成です。疑問点・翻訳ミスを始めとした指摘がありましたら、どしどしお願いします(14/12/18)。
1週間あるから大丈夫だろうとたかを括っていたら、あっという間に投稿日になってしまいました。本当はPylearn2を使ってRBMを学習させようと考えていたのですが、役に立つ内容を書くには時間が足りなさすぎるので、お茶を濁します。
今回の目標
- Restricted Boltzmann Machine及びDeep Belief Networkの基本的な動作原理を知る
- "A Practical Guide to Training Redstricted Boltzmann Machine"(GE Hinton, 2012)で黒魔術(RBMの性能を引き出すコツ)を学ぶ
先日、以下のような発表をしました。今回の内容は以下のスライドの焼き直し・改良を含みます。参考にどうぞ。
RBM(Restricted Boltzmann Machine)とは?
**RBM(Restricted Boltzmann Machine)**とは、Deep Learningにおける 事前学習(Pre Training)法の一種で、良く名前を聞く AutoEncoderと双璧を為すモデルの1種です。統計力学に端を欲し、1984年~1986年にモデルが考案されました。入力を受けて出力が 決定論的(deterministic) に決まるAutoencoderとは違い、議論を確率分布の上で行える 生成モデル であるため、利便性の高いモデルとして知られています。
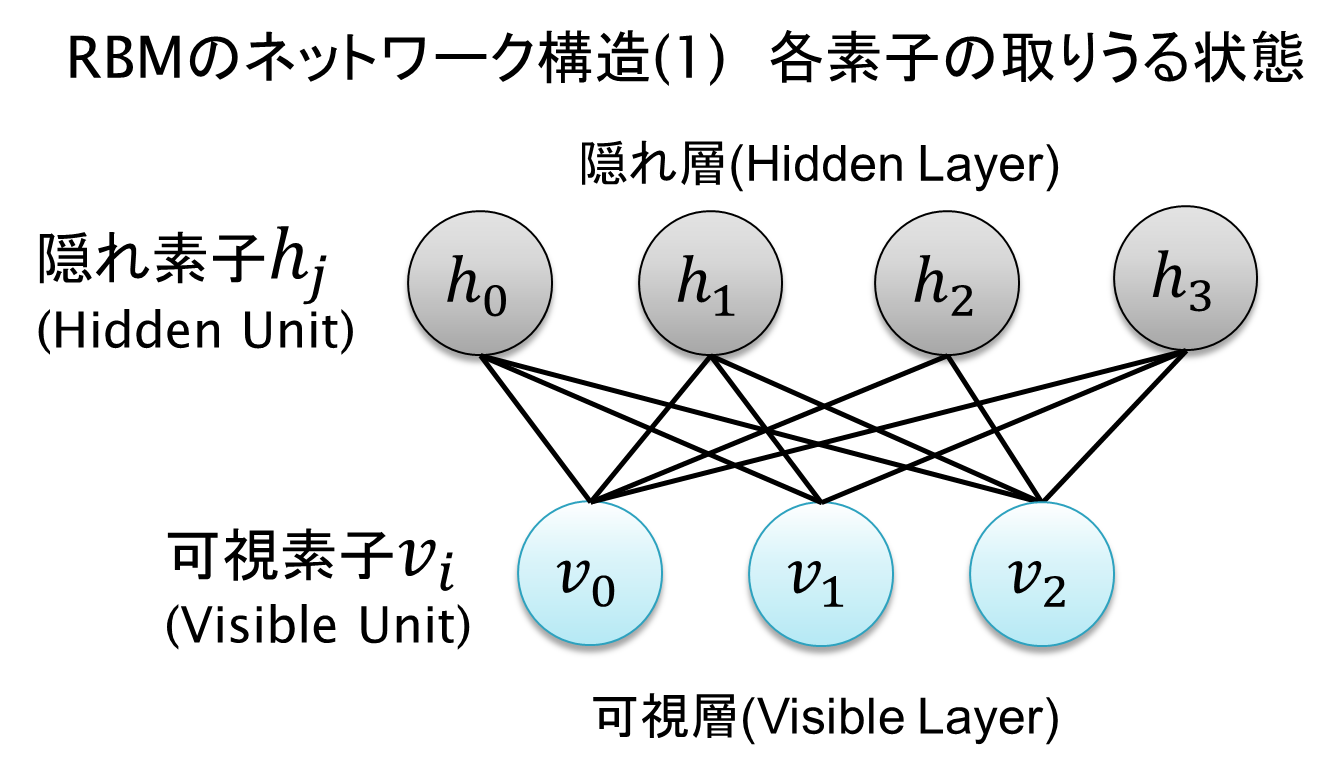
RBMは2層構造のネットワークを構成しています。それぞれの層は 可視層(Visible Layer) と **隠れ層(Hidden Layer)**と呼ばれます。可視層に入力データを入れて学習させると、隠れ層に入力データの特徴(Feature)を良く表すようなパラメータが学習されて出てきます。なぜ **Restricted(制限された)**と言われるかというと、ネットワークの接続を可視層対隠れ層のみに限定しているからです。これによって計算量を現実的な水準に落としています(とはいえ、これでも理論的には計算量が爆発します)。
以下に図を示します。
通常、可視素子$v_i$や隠れ素子$h_j$には 0または1(2値、binary)が入ります(勿論、モデルを少し変えれば他の値を入れることもできます)。
ここで、生成モデルについてかじった人なら、「折角確率を求めているのに、何故0と1しか入らないことになっているんだ?」と混乱する方もいらっしゃるかもしれませんが、ある訓練データ$\textbf{v}$が与えられたとき、条件付き確率$p(h_j=1|\textbf{v})$が計算でき、その意味は「$\textbf{v}$が与えられたとき $h_j$がONになる(1になる)確率 」ということです。
この条件付き確率は次に紹介する重み(Weight)、バイアス(Bias)の値によって変わっていきます。学習を進めると、新しいデータ$\textbf{v}_{test}$が与えられたときに vの特徴を抽出した何か が$\textbf{h}$ に01001...といったベクトルの形で浮き出てくるわけです。
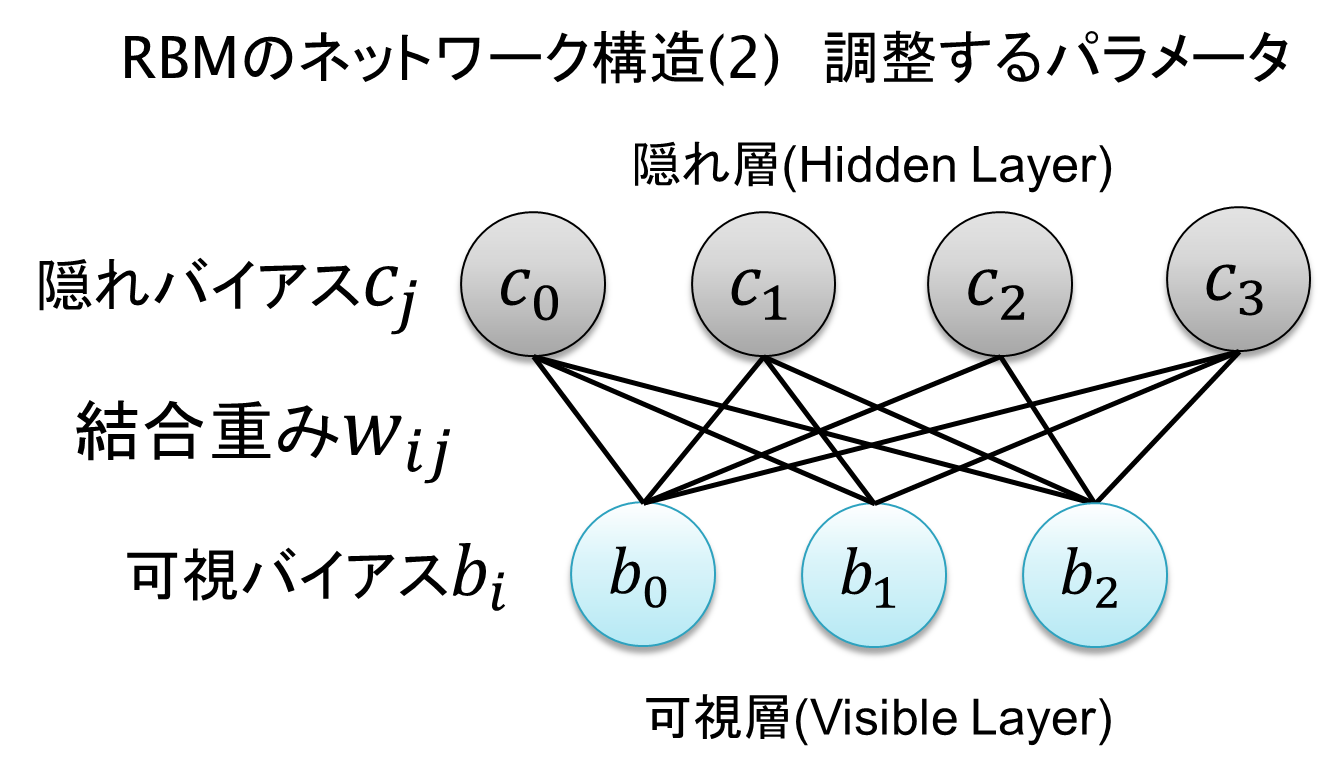
RBMのパラメータは大きく2種類あります。
1つ目が、各素子に付随するバイアス$b_i, c_j$
2つ目が、可視層と隠れ層から1つずつ素子を選び出した際の結合の強さ(重み)を表す$W_{ij}$
になります。これらを学習データの入力を元に教師なし学習させることで、RBMの学習が完了します。
DBN(Deep Belief Network)
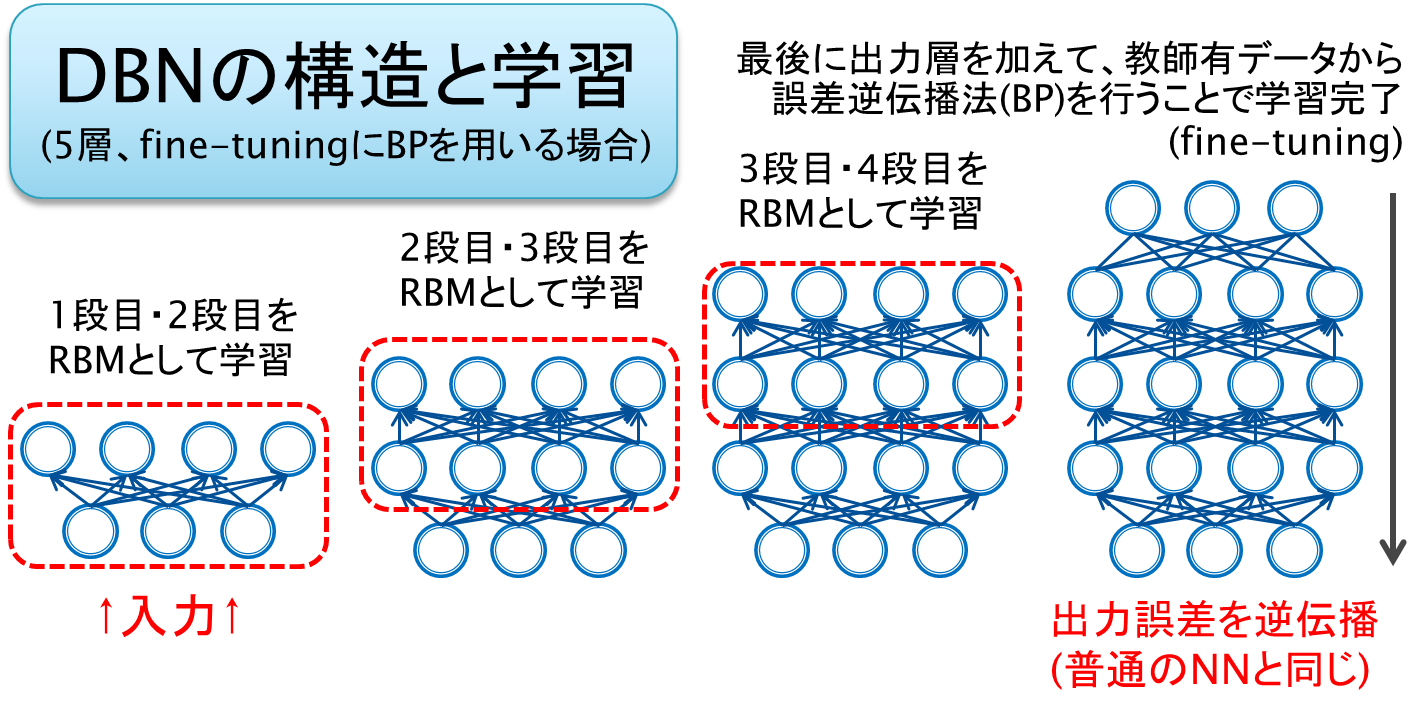
しかしながら、RBMは先に述べたとおり2層構造なので、これはDeepな構造とは言えません。そこで、 RBMを多数重ねて 、下の層から順にRBMを1つずつ学習させるというアイデアが出現しました。こうしてできた多層のネットワークは **Deep Belief Network(DBN)**と呼ばれます。DBNは2006年にGeoffrey Hintonが発表したモデルで、これが今日まで続くDeep Learningブームの火付け役となったのです。DBNは以下のような図で表すことが出来ます。発展系としてDeep Boltzmann Machine(DBM)が存在します。
今回の範囲を超えるので詳しくは取り扱いませんが、上図右のように出力層を載せたあとは線形回帰やSVMといった標準的なアルゴリズムで教師有学習をさせても性能が上がります。多数の段数を経ることにより入力データの時点では明確でなかった「特徴」が抽出されているのです。
RBMの学習の流れ
RBMのモデル(2値変数の場合)
E(v,h)=-\sum_{i}b_iv_i-\sum_{j}c_jh_j-\sum_i\sum_jv_iW_{ij}h_j
p(v,h)=\frac{1}{Z(W)}exp(-E(v,h))
RBMのモデル構造は見慣れない形ですが、至ってシンプルです。エネルギー関数Eは先の可視素子、隠れ素子の取りうる値によって形が変わります。ただ、これでは確率分布にならないので、正規化係数Z(W)を取って確率分布の形にします。
RBMの学習の最終目標は、 $p(v)=\sum_jp(v,h)$の最尤推定です。与えられた訓練データ$v$を$p(v,h)に放り込んで、 データ点とあてはまりが尤も良くなる分布を考えるのです。$h$は隠れ変数なので総和を取って消去します。
最尤推定では、お分かりですね、尤度の対数をとって、それを 最大化 します。当然解析的に数式をこねくり回して解けるようなモデルではないので、勾配降下法(Gradient Descent)を使います。微分が必要になります。詳しく数式を追うのは避けますが、対数尤度の任意のパラメータに対する勾配
\frac{\partial J}{\partial \theta}=-\sum_v\sum_h\frac{\partial E}{\partial \theta}p(h|v)q(v)+\sum_v\sum_h\frac{\partial E}{\partial \theta}p(v,h)\\
但し、q(v)=\frac{1}{N}\sum_k\delta(v-v^k) (Nは訓練データ点の数、v^kは訓練データのベクトル)
を計算する必要が出てきます。この式に少し注目しましょう。
第1項第2項共にv, hに対し総和を取っています。これはほぼ積分と考えて差し支えありません。
第1項では条件付き分布が含まれていますが、RBMのネットワーク構造の制約によって、$p(h|v)$の計算は かなり容易 です。$q(v)$も0か1/N、しかもN通りしか有限値をとらないので、簡単に計算することが出来ます。これは データ依存の成分です。
一方第2項では一切計算が簡単になる要素がありません。定義した モデル依存の総和です。値の制約もないので、すべてのv,hに対する総和を取る必要があります。この計算の計算量は指数的に増加するため、 サンプリングによって近似的に第2項を計算することになります。
サンプリング手法としてはMCMCを利用したMetropolis法などが有名ですが、RBMの学習に於いては次節のCD(Contrastive Divergence法)を使います。
※上の勾配などの導出は
Restricted Boltzmann Machineの導出に至る自分用まとめ
に譲ります。とても分かりやすいです。
CD(Contrastive-Divergence)法
CD法は、2002年にHintonによって考案され、上の勾配法を少ない計算量で行わせることが出来るようになりました。アルゴリズムは非常に簡単です。
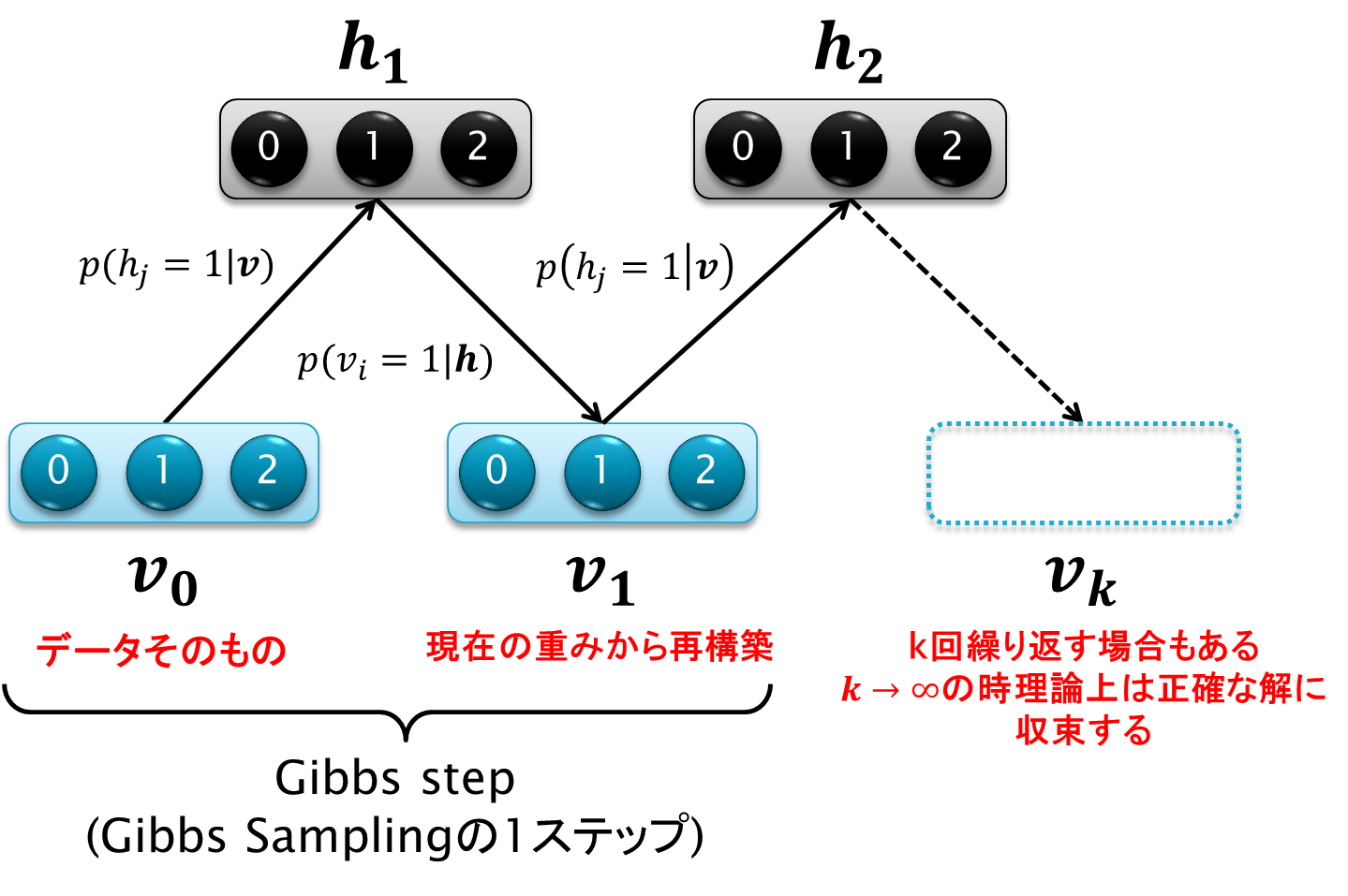
上図はCD法のイメージ図を表します。サンプリングメソッドを知っている方なら、「サンプリングというんだから、たくさんのサンプルを生成してその期待値を取るんでしょう?」と仰るかもしれませんが、CD法では通常1回、多くとも数回しかサンプルを取りません。アルゴリズムは以下のようになります:
- 初期値$v$としてある訓練データ$v_0$を選びます。
- 条件付き確率$p(h_j=1|v)を用いて隠れ層$h$の値を各素子ごとにサンプリングします。
- 条件付き確率$p(v_i=1|h)を用いて可視層$v$の値を各素子ごとにサンプリングします。
- これを全てあるいは一部のデータ点に対して行い、
p_{recon}(v,h)=\frac{1}{N}\sum_i\delta(v-v_k^i)p(h|v_k^i)
を上の第2項の微分を除く総和の代わりとして使う。
以上です。1回しか2~3のサンプリングの工程を行わない場合をCD-1法、k回行えばCD-k法と呼ばれます。kを無限に繰り返せばいつかは正確な総和にたどり着けますが、CD法は正確から程遠い恐ろしい近似で済ませてしまいます。ただ、この方法で経験的に上手く学習ができることが分かっています。
ここまでつらつらと話してきましたが、ここで重要なのはRBMは
非常に大ざっぱで不正確な近似をアルゴリズム中に孕んでいる
という事実です。勾配の更新は概ね良い方向に向かいますが、その挙動は複雑怪奇なものになります。この事実を良く受け止めておいてください。
Deep Learningにおけるトレードオフとは?
上のCD法は最も極端な例になりますが、Deep Learningで用いられているコンポーネントの多くは、非凸な関数を最大化するといった **最適化問題(Optimization Problem)**を解決するために様々な工夫を凝らしています。その結果、今まで解けなかった問題が多数計算可能になったのですが、時にはスピードを得るために正確な計算を犠牲にしたものが出てきたのです。Deep Learningは「正しい学習」と「大ざっぱで高速な学習」とのきわどいバランスによって成り立っています。
Deep Learningのタブー
Deep Learningは、
- データが持つ潜在的な特徴を自動的に学習する(タスク固有の職人技が要らなくなった)
- 高度な表現力を維持しつつ、過学習を大幅に抑制
というその特性と、「Googleの猫」を始めとする素晴らしい成果をもって、今年は一般の人々にも **「ディープラーニング」**という名前が知れ渡ることとなりました。
(例えば:「ディープラーニング ビッグデータが切り開く、新世代の人工知能(AI)」(朝日新聞 2014年6月20日朝刊)
その先頭を走るHInton, Bengio, Ng, LeCunといった諸先生方は、すさまじいペースで論文を出版し続けています。企業の支援を受けて、その勢いは留まるところを知りません。
しかしながら、それらの論文中で中々触れられないところがあります。それは、モデルの複雑性による パラメータ数の爆発です。PRMLなどを読んでいると、回帰問題における正則化係数の設定や、事前分布の超パラメータの設定に関して「(数個とはいえ)自分で良いパラメータを探す必要がある」と既に指摘されているのに対し、Deep Learningにおけるパラメータの数は 数百にも上ります。正直、今までの感覚からすれば 論外です。
今記事で取り扱う"A Practical Guide to Training Redstricted Boltzmann Machine"(GE Hinton, 2012)によると、CD法を用いたRBMの学習には、以下のパラメータや関数の設定が必要となるそうです。DBNにして多層にすれば、当然パラメータの数はその層の数に比例、組み合わせの数は指数的に増加していきます。
どのようなパラメータが存在するのか?
◆勾配法に関するパラメータ
- 学習率
- モーメンタム
- 荷重減衰
- ミニバッチ勾配法(Mini-Batch-Gradient-Descent)のバッチサイズ
◆RBMの構造に関するパラメータ
4. スパース乗数
5. Sparsity Target
5. 重みの初期値
6. RBMの隠れ層の数
◆パラメータ以外に考慮する要素
- 入力データの前処理
- 活性化関数の選択
- 状態を確率的(stochastically)に更新するか、あるいは決定論的(deterministically)に更新するか
- 各訓練データに付き何回隠れ層の値を更新すべきか
- CD法による更新を訓練データ点から始めるべきか否か
- いつ学習が収束したと判断するか
◆学習の監視に関する要素
- どの値をもってモデルの性能を判断するか?
- 正しく学習しているか監視するには何を見ればよいか
特に学習率、荷重減衰、モーメンタムは良くわからない方も多いかもしれませんが、勾配降下法の式を拡張して、より素早く収束するように工夫するためのパラメータとして存在しています。更新式は以下のような形になります:
\theta^{(t+1)} = \theta^{(t)} + \eta \frac{\partial}{\partial\theta^{(t)}} \Bigl(\sum_{i=1}^{N} ln \mathcal{L}(\theta^{(t)}|x_i)\Bigr)-\lambda\theta^{(t)}+\nu\Delta\theta^{(t-1)}
$\eta$:学習率(learning rate)…勾配をどれだけ動かすか
$\lambda$:荷重減衰(weight decay)…不要に重みが爆発するのを防ぐためのペナルティ項の係数
$\nu$:モーメンタム(momentum)…重みの振動(後述)を防ぐための項の係数
1つ改めて知っておいてほしいのは、 Deep Learningは何でも学習できる魔法の杖ではないということです。例えば、DBNの層の数を決定するにあたって、明確な基準はありません。使用するデータ及びそのタスクに強く依存します。層の数に対してデータがより複雑であればモデルがその複雑性をつかみきれず悪い性能を出しますし、 データの構造が単純すぎる場合であっても、パラメータの調整に失敗してゴミが出力されてしまいます。Deep Learningは100万枚の画像から特徴を抽出する作業をやってくれますが、その性能を引き出すには 人間の経験と勘が不可欠となります。
"A Practical Guide to Training Redstricted Boltzmann Machine"(Hinton, 2012)を読む
さて、本題です。この論文では、RBM考案者のHinton先生自らパラメータを設定する際のヒューリスティックな知識を披露してくれています。3章から淡々とパラメータとそれに対する処方箋を紹介しています。やや冗長な所は省きながら和訳しています。筆者の理解度の関係で訳が曖昧な所は **敢えて英語を残しています。**ご容赦ください。素人翻訳なので、翻訳ミスの指摘等大歓迎です。
章番号は2010年版(2012年版もあります)に従っています。
処方箋には、最終的に適用すべきアドバイスが書いてあります。まずはそこを読むとよいでしょう。筆者の解釈によるサマリーも最後に載せています。
3. CD法使用時にどのようにを統計量を収集していくのか?
前提:
可視層隠れ層共にbinaryの場合を考える、可視層に対する最も良い生成モデルを作ることを考える。
Deep LearningをDBNの形で実装する際は、各層でRBMを学習させたのち
3.1 隠れ層の更新
前提:隠れ層の更新では、可視層の情報と条件付き確率$p(h|v)$を用いて$h_j$を何らかの基準で決定する
通常、隠れ素子はシグモイド関数で表される確率が一様乱数より大きい場合にONになる。
この際、それぞれの隠れ素子の状態をbinaryに扱うのは非常に重要である。もし隠れ素子の情報として連続値が用いられれば、次に可視層が更新されるときに連続値が用いられるということになる。これは 隠れ素子は(平均して)たかだか1bitの情報しか伝えられない という事実を無視することになる。このボトルネックは強いRegularizerとして機能する。
隠れ素子の最後の更新時に、stochastic(確率的)binary states(0か1か?)を使うのはばかげている。何故なら、0か1か選択することで依存するものなど存在しないからだ。そこで、確率自身を用いることで無駄なサンプリングノイズを回避する。
CD-n法に於いては、 最後の隠れ層の更新時 のみ確率を用いるべきである(それ以外の更新では、確率に応じて状態が0又は1になるよう調整すればよい)。
3.2 可視層の更新
可視層もbinaryであるという前提に立てば、可視層の更新も確率的に0か1を選択する作業となる。しかしながら、 一般的には0か1の代わりに確率p_iをそのまま使うことが多い。これは入力データに依存する隠れ層と対照的に、サンプリングノイズを軽減し、結果としてより良い学習が可能である。RBMの学習のみを考えるとやや悪いモデルに収束する証拠(Tijmen Tieleman, personal communication, 2008)があるが、DBNのPre-Trainingとして使う分には問題にならない。
3.3 学習に必要な情報の収集
前提:可視層の素子の値の更新結果に連続値を使用する(3.2を参照)
その場合、RBMの忠実なモデルであるよりも、を用いたほうがサンプリングノイズが少ない→高速に学習できることが分かっている
訳注:第2セクションを省略しているため、やや唐突な議論になっている。上式は、
\frac{\partial J}{\partial \theta}=
-\sum_v\sum_h\frac{\partial E}{\partial \theta}p(h|v)q(v)+\sum_v\sum_h\frac{\partial E}{\partial \theta}p(v,h)=
\langle v_ih_j\rangle_{data} - \langle v_ih_j\rangle_{model}
の第1項$\langle v_ih_j\rangle_{data}$の条件付き確率$p(h|v)$及び$p(v|h)$中の$v_i$や$h_j$を$p_i$、$p_j$と書き換えて使用するという意味である。
3.4 CD-1法の学習データを得るための処方箋
注:CD-1法(CD-n法ではない)に対する処方箋であることに注意
①隠れ層の更新:
$\langle v_ih_j\rangle_{data}$(上式の第1項):常に各素子$h_j$に0または1の値を与える(stochastic)
$\langle v_ih_j\rangle_{model}$(上式の第2項): 各素子$h_j$の値に連続値を使う(サンプリング不要)
②可視層の更新:
($p(v|h)$でロジスティック関数を用いるという前提において)データ項(第1項)、再構築項(第2項)共に確率を使う。
確率を直接用いる場合、ランダム性が失われるため、初期値をランダムにして対称性を破ること。
4. ミニバッチ勾配法の大きさ
普通のGD: 1個ずつ更新
ミニバッチ:10~100個ずつ更新
行列積の計算がGPUに良いという根拠あり
平均の取り方に関する議論:学習率とbatch sizeを完全に分離する
4.1 処方箋
データセットが等しいと考えられる少ないクラスを含むと考えられるなら、mini-batchはクラス数と同じにすることが多い。さらに、mini-batchのサンプルは必ず各クラスに属するサンプルを用いるとよい。その結果、勾配を予測するサンプリング誤差が小さくなる。それ以外の場合(クラス数が多岐にわたる場合)は、訓練データ点をランダムに並び替えたうえ、10個程度でサンプリングを行うとよい。
5 学習状況の可視化
二乗和誤差はその簡便さからRBMの学習においてもデータとReconstructionの二乗和誤差をモニターすることは多い。
RBMではサンプリングによる潜在的誤差があるので、初期の大幅な減少のあとは振動しながら少しずつ減少する。
ただ、便利な割にこの指標は 「学習状況の可視化」においては非常に貧弱な指標である。 なぜなら、CD-n法(特にn >> 1の場合)に二乗和誤差の最小化=最適化を試みている関数では 全くない 上に、学習中に2つの要素が同時に変化しているからである。
1つ目:RBMの平衡状態(収束状態)における分布と実験により得られた学習データの分布
2つ目:交互に行われるギブスマルコフ連鎖の混合率(Mixing Rate)。
2つ目がたまたま小さかった場合、1つ目の誤差がかなり大きい場合でも、観測できる二乗和誤差が小さく見えてしまう場合がある。学習の過程で緩やかに2つ目が下がっていく場合もあるので、1回限りの緩やかな誤差の減少に期待することはできない。一方で、少し誤差が増えた程度で過剰反応する必要はなく、学習が進行していることすらあある。当然ながら、誤差が急激に上昇のは悪い傾向である。
注:ここでいう「混合率」とは、「(訓練データから始まった)サンプリング列が求めたい収束分布にどれだけ早く近づくか(要は、どれだけ素早く近似するか)」を表す指標である。(資料が少ないので正確な理解ではないかもしれないが)具体的な値を表すものではなく、かなり相対的な基準である。
5.1 再構築誤差を使用するにあたっての処方箋
「使用はするが、信用してはいけない」。正確に何が起こっているか知りたければ、セクション15の複数のヒストグラムを用いる方法を参照のこと。ALS(Annealed Importance Sampling)でデータの密度(尤度)を推定することが出来る。セクション16で解説するラベル付きデータの結合密度モデルを学習しているなら、discriminative performance on the training data and on a held out validation setをモニタリングすることを考えること。
6 過学習のモニタリング
生成モデルを学習させる際は、とりあえずモニターする自明の量として、現在のモデルをデータ点に割り当てた際の確率がある。検証データ(validation data)に対する確率が減少を始めるタイミングが、(過学習が始まるギリギリのタイミングという意味で)学習を終わらせる地点である。ところが、不運なことに、規模の大きいRBMにおいてこの確率を計算することはかなり難しい。分配関数(partition function)の存在である。それでも、訓練データと検証データに対する自由エネルギーを比較することで過学習をモニターすることが出来る。この際、partition functionはcancel outされる。データベクトルに対する自由エネルギーは隠れ層の数に比例して計算できる。(16.1参照)全く過学習の減少が起こっていなければ、自由エネルギーは訓練データと検証データでほぼ同じになる。この値にギャップが出てき始めたころが、過学習の開始タイミングである。
6.1 処方箋
いくつかのテクニックを使って、一部の訓練データに対する平均自由エネルギーを計算して、検証データに対するそれと比較するとよい。両者の間に差が出てきた時が過学習の状態であるが、それ以上にエネルギー関数が減少(モデルが良くなってきている)のであればまだ続けるべきである。当然、選ばれる訓練データは常に同じものであり、同じ重みを使用することを前提とする。
7 学習率
学習率が大きすぎれば、再構築誤差は通常急激に増加し爆発する。
もしネットワークが普通に学習する程度まで学習率を落としたとすると、誤差は顕著に下がってくる。ただし、これは必ずしも良いこととは言えない。その原因の一部として、確率的重み更新中の小さな誤差が蓄積して、結果として長い目で見ると余計に学習時間がかかってしまう、ということがある。学習の終わりでは、しかしながら、概して学習率を下げるという犠牲を払う必要がある。複数回の更新における重みの平均を取るという考え方を用いることは、(学習率の調整以外の)代わりにノイズを取り除く手段となる。
7.1 処方箋
学習率を大ざっぱに計算する良いルール(Max Welling, personal communication, 2002)として、重みの更新及び重みのヒストグラムを見ることである。重みの更新量は重みそのものの$10^{-3}$倍であるべきである。ユニットにとても大きい入力があるのであれば、更新量は小さくするべきだ。なぜなら、 many small changes in the same direction can easily reverse the sign of the gradient. Conversely, for biases, the updates can be bigger.
8 重みとバイアスの初期値
重みは概して平均0、標準偏差0.01程度のガウス分布から得られるランダムの小さな値に初期化されることが多い(Random Initialization)。値を大きくすれば初期の学習を高速化できるが、時として最終的なモデルの性能が落ちることがある。重みの初期値は隠れ層の出力に用いる確率が1や0(学習を顕著に遅くする原因)に大きく近づかないように注意する必要がある。もし(binaryではなく)確率を更新に用いるのであれば、重みの初期値は全て0でも構わない。なぜなら、同じ結合であっても確率中に含まれるノイズが隠れ層の状態をそれぞれ変化させるからである。
一般的に、可視素子$v_i$のバイアス$b_i$を$log[p_{i}/(1-p_{i})]$($p_{i}$は訓練データのうち素子iがON(1)になっているデータ点の比率)とすると上手くいく。この手順を踏まない場合、学習の初期において隠れ層が不正確な$p_i$を用いて同様のバイアス調整を肩代わりすることになる。
Sparcity target probability of t(セクション11)を使うのであれば、隠れ素子のバイアスを$log[t/(1-t)]$とすると役に立つ。そうでなければ、隠れ層のバイアスは0でも良い。隠れ素子の値を極めて絶対値の大きい負の値にすることによってsparcityを無理やり促進させることもできる。
8.1 処方箋
重み$W_{ij}$:N(0, 0.01)からランダムに初期化すればよい。
可視層バイアス$b_i$:$log[p_{i}/(1-p_{i})]$($p_{i}$は訓練データのうち素子iがON(1)になっているデータ点の比率とする)
隠れ層バイアス$c_j$:初期化の方法よりも、隠れ素子が常に0か1になっていないか頻繁にチェックすることが重要
9 モーメンタム
モーメンタムは 目標関数が長く、狭く、直線的で、なだらかだが一貫している勾配が谷底に、より急な勾配がその谷の側面に広がるような(要はU字型)の谷がある際に学習スピードを速くすることが出来る方法である。モーメンタムの理論は重い球が表面を転がり落ちていくことをシミュレートする。ボールはスピードの増加方向に谷底を滑っていくが、お互いの緩い勾配が時間を経るにつれ互いの勾配の効果を打ち消すため、谷の線を沿わずに(振動しながら)進んでいく。推定された勾配と学習率との積をパラメータの値を増加させるために使う代わりに、モーメンタムはその値を速度$v$を増加させるために使われ、現在の速度がパラメータの値を増やすために使われる。
ボールの速度は時間が経つにつれて減衰するようになり、超パラメータ「モーメンタム」、$\alpha$は新しいミニバッチにおける勾配を計算した後の以前の速度の一部を為す:
\Delta\theta_i(t)=v_i(t)=\alpha\ v_i(t-1)-\epsilon\frac{dE}{d\theta_i}(t)
もし勾配が一定の値を保つのであれば、最終速度は$\epsilon\ dE/d\theta_i$を因数$1/(1-\alpha)$をもって上回る。この因数は0.9のモーメンタムに対して10を取り、この値(0.9)がこの超パラメータの典型的な設定となる。モーメンタム法による一時的なスムージングは、谷における末広がりの(divergent)振動を単純に学習率を因数$1/(1-\alpha)$をもって増加させることで回避させることが出来る。
モーメンタム法はパラメータを必ずしも最適(最も急な勾配)な方向に動かないようにさせるため、共役勾配法(conjugate gradient)と類似した性質を生み出すが、前者の方がより単純である。各パラメータに対し可変のパラメータを設定する方法と異なり、モーメンタムは谷が必ずしもパラメータの軸にそっていない場合に対しても良く機能する。
モーメンタム法を別の見方から見る方法(Tijmen tieleman, personal communication, 2008)は次の通りである:それは学習率を因数$1/(1-\alpha)$によって学習率を増加させるものの、実効的な勾配の見積もりを指数的に減少する関数に従う割合で遅らせることと等しい(It is equivalent to increasing the learning rate by a factor of 1/(1−α) but delaying the full effect of each gradient estimate by dividing the full increment into a series of exponentially decaying installments)。これは系が入力の増加を実際に受ける前に、事前に対立する勾配の方へ動く時間(猶予)を与える。これが、裏を返せば、不安定な振動をもたらさずに学習率を上げることを許容する。
9.1 処方箋
モーメンタムはまず0.5に設定するとよい。再構築誤差は初期のプロセスで大きく減少する。現象が穏やかになったら、モーメンタムを0.9に増やそう。この際、一時的に誤差が増えることがあることに注意しよう。もし誤差の変化が不安定になるようであれば、安定するまで2倍ずつ学習率を徐々に下げること。
10 荷重減衰
荷重は通常の勾配に対して追加項を加えることで機能する。その追加項は大きい重みに対しペナルティを与える関数の導関数である。「L2」と呼ばれる、もっともシンプルなペナルティ関数は、重みの2重和の半分に「重みコスト」と呼ばれる係数を乗じたものである。
重要なのは、ペナルティ項の導関数に対して学習率の値をかけることである。さもなくば、学習率の変化は、最適化の手順を変えるのではなく、最適化の対象となる関数自身を書き換えてしまうことになる、
RBMにおいて荷重減衰を用いる理由は4つある。1つ目は、訓練データに対する過学習を抑制することで、新規のデータに対する汎用性をより持たせることが出来るということだ。2つ目に、無駄な重みを縮小させることにより、隠れ層の受容野をより滑らかに、解釈しやすくすることができる。3つ目は、(荷重減衰を導入することで)学習の初期に導入された、常にがっちりONまたはOFFの状態にあるような、非常に強い重みをもつ隠れ項を「切り離す」ことが出来るということだ。そのような素子に再度性能を出してもらうようにするより良い方法として、次節で導入される「スパース化目標」を導入するという手法がある。
4つ目の理由は、この学習によってギブスサンプリングを用いるマルコフ連鎖の混合率(mixing rate)が改善するということだ。小さい重みに対しては、マルコフ連鎖はより速く混合する。CD法の手順はマルコフ連鎖の後半に出現する派生項?(derivatives)を無視するという発想に立っている(Hinton, Osindero and Teh, 2006)。そのため、混合が素早く進むとき、最大尤度をよりよく見積もるようになる。無視された派生項はこの際以下の理由により小さい:マルコフ連鎖が定常分布に非常に近いとき、連鎖からサンプルする最良のパラメータは現在のパラメータと非常に近いからだ。
「L1」と呼ばれる異なる形の荷重減衰は重みの絶対値の和の導関数を用いる。 これはしばしば多くの重みの値を0にしたうえで、その他のいくつかの重みを大きくさせる。 これは重みを解釈することをより容易にさせる(疎な構造を形成する)。画像に対する特徴を学習する際、例えば、L1荷重減衰は強く局所化された受容野を持つことにつながる。
重みの大きさを制御する別の方法としては、各素子の重みに対し、 絶対値の和又は二乗和を許容される上限値として課すという方法がある。各素子の重みの更新の後、各重みは上限値を超えた場合に修正される。この修正によって隠れユニットが非常に小さいを持ったまま行き詰まるのを防いでくれるが、(次節で紹介する)スパース目標を導入する方がこの問題を解決するより良い方法となる。
10.1 処方箋
RBMに対しては、L2 weight-decayに対する常識的な値は一般に0.01~0.00001の間に位置する。隠れ層及び可視層のバイアスには通常荷重減衰をかけない。なぜなら、バイアスはあまり過学習しないからである。むしろ、バイアスの値は大きくなる必要がある。
初期のペナルティとして0.00001を試そう。もしAIS(Annealed Importance Sampling)をvalidation setに対する密度の推定に使っているのであれば、2倍ずつペナルティ項を増やしていって密度を最適化する。ペナルティ項を少々変更した程度では性能に大きな影響を与えることはない。もしvalidation setに於いてdiscriminatice prerformanceをテストさせるような結合密度モデルを学習しているのであれば、この方法はペナルティ項を調整するために使われるだろう。しかしながら、それ以外のケースでは、荷重減衰が過学習を予防するためだけの項ではないことに留意すべきだ。荷重減衰によって、mixing rateが増え、その結果としてCD法においてより大きい尤度を示してくれる。そのため、過学習の懸念がない場合(データ量が非常に大きい場合)であっても、荷重減衰は役に立つ。
11 スパースな発火の促進
めったに活性化状態になることのない隠れ素子は過半数の場合に発火するような素子と比べると一般的に解釈が容易である。さらには、稀にしか発火しないfeatureを使うことで、時には識別性能(discriminatve performance)が改善することもある。
2値隠れ素子のスパース性は、スパース化目標(sparcity target)と呼ばれる、期待される活性化確率p<<1を明示化することで達成することが出来る。追加項として、実際の活性化確率をpに近づけるための項qが導入される。qは、各ミニバッチにおいて、素子が活性化状態にある期待値の指数関数的に減衰する平均を用いることによって見積もることが出来る(?):
q_{new}=\lambda\!q_{old}+(1-\lambda)q_{current}
$q_{current}$は現在のミニバッチにおける隠れ層の平均活性化確率を示す。
ペナルティ項として適当な指標は、期待される確率分布と実際の確立分布の間の交差エントロピーであり:
Sparsity\ \ penalty \propto -plogq-(1-p)log(1-q)
ロジスティックユニット(注:2進(binary)素子を使用時)においては、上の式はthe total input to a unitに対し、$q-p$という簡単な微分の形を持つ。この微分は、スパース化コスト(sparsity-cost)と呼ばれる超パラメータによってスケールされており、各隠れ素子のバイアスと入力重み(incoming weights)両方を調整するために用いられる。重要なのは、(バイアスと重み)両方に対して同じ微分を用いるということである。例えば、バイアスは一般に、隠れ素子の活性をスパースにするためにより減少する方向に向かっていくが、一方で重みはユニットの影響力を増やすためにより重みを増やす方向に動こうとする現象が起こる。
11.1 スパース性に対する処方箋
スパース化目標(sparsity target)を0.01から1の間に設定しよう。qの推定値に関する、(各素子のスパース化を進める)減衰係数$\lambda$を0.9から0.99の間に設定しよう。隠れ層の平均活性化確率をヒストグラムに出力し、隠れ層の活性化確率の期待値が目標の近辺に近づくようにスパース化コスト(sparsity cost)を調整しよう。もし確率が目標確率に対し強く密集しているなら、スパース化コスト(sparsity cost)を減少させて、本来の目標であるモデル本体の学習の妨げにならないようにする。
12 隠れ素子の数(The number of hidden units)
識別モデルにおける機械学習から得られた直観を隠れ素子の数を考える上での材料にするのは悪い方法である。識別モデルにおいては、訓練データに課されるべき制約の量は、訓練データから適切なラベルを割り振るのに必要なビット数に等しいと考えられている。ラベルは通常非常に小さい情報量しか持たないため、訓練データに対し多数のパラメータを持たせることは、得てして深刻な過学習の問題をもたらすこととなった。高次元データの生成モデルを学習させる場合は、もっとも、 データベクトルを表現するためのビット数こそがモデルのパラメータにおいてデータに課されるべき制約となる。これは、ラベルを特定するために必要なビット数と比べると必要な桁数が数桁多くなる。よって1000ピクセルを持つ画像が10000枚あるような場合は、100万個のパラメータを当てはめることが極めて合理的な選択となる。これは1000個もの全接続された隠れ素子を導き出す。もし隠れユニットの接続が局所的であったり、重みを共有したりしているのであれば、より多くの隠れ素子を使っても良い。
12.1 処方箋
学習中、またはテスト中において主な問題が計算量よりも過学習にある場合にあるならば、「もし十分に良いモデルを使用しているのであれば、各データベクトルを表現するのに何ビット使うか」を見積もってみよう(すなわち、良いモデル下におけるデータベクトルの(2を底とした)情報量を見積もってみよう)。そうして見積もった値と訓練データ数で掛け算を施し、その10倍ほど小さい値?(a number of parameters that is about an order of magnitude smaller)をパラメータ数として使用しよう。もしスパース化目標確率をかなり小さく設定しているのであれば、より多くの隠れ素子数を持たせても良い。(非常にデータ量の大きいデータセットにありがちな)冗長な訓練データを用いている場合は、かえって少ない素子数を設定する必要がある。
13 2値素子以外の様々な素子
RBMはもともと2値の値を用いる可視素子及び隠れ素子を用いるために作られたが、その他多くの種類の素子を利用することもできる。(Welling et al, 2005)において指数型分布族に属する素子の取り扱い方が与えられている。これらの素子は2値素子(あるいはロジスティック活性化関数)において十分にモデル化を行うことが出来ないデータに対して利用される。
13.1 ソフトマックス・多項式素子
2値素子に対しては、活性化確率(注:条件付き確率$p(h_j=1|\textbf{v})$は入力の合計$x$を用いて、以下のロジスティックシグモイド関数で表される。
p=\sigma(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+e^0}
この素子によってもたらされるエネルギーはON(1)の時$-x$で、OFF(0)の時0である。上式(式15)は、各(2つの)状態における確率はエネルギーの負の指数に比例していることを明確に表している。これはK状態に対して一般化することが出来る。
p_j=\frac{e^{x_j}}{\sum_{i=1}^{K}e^{x_i}}
これはしばしば"ソフトマックス"素子と呼ばれる。これは順序性を持たないK個の状態に対する値に対する適当な方法である。ソフトマックスでは、2値素子がいくつか制限をもって組み合わされて、K状態のうちちょうど1つがONでその他がOFFである場合として見ることができる。このような見方をした場合、ソフトマックス中における2値素子の学習は、通常の2値素子によるそれと全く同一である。唯一の違いは各状態における確率の計算法とサンプルの取り方である。
ソフトマックス素子の更なる一般化として、(確率分布の入れ替えをもって)1回のサンプリングの代わりにN回のサンプリングを行うという考え方がある。K個の各状態は(注:ソフトマックスでは1つの素子が1であることしか許さなかったのに対し)1より大きい整数を取ることが出来るが、その合計値はNにならなければならない。これは多項式素子と呼ばれ、繰り返すように、学習の流れそのものは2値素子と変わらない。
13.2 ガウシアン可視素子
現実世界の画像の集合(patches of natural images)や音声を表現するために用いられるメル周波数ケプストラム係数(Mer-Cepstrum coefficients)のようなデータに対しては、ロジスティック素子は非常に表現力の乏しいモデルとなる。そこで、2値の 可視素子を独立したガウシアンノイズを持つ線形素子に置き換えるという手段が1つの解決法となる。エネルギー関数の形は次のように変わる:
E(v,h)=\sum_{i\in\ vis}\frac{(v_i-a_i)^2}{2\sigma^2_i}-\sum_{j\in\ hid}b_jh_j-\sum_{i,j}\frac{v_i}{\sigma_i}h_jw_{ij}
$\sigma_i$は可視素子$i$に対するガウシアンノイズの標準偏差を示す。(注:各素子が別々の$\sigma$を持っている)
各可視素子についてノイズの分散を学習することは可能であるが、CD-1法では難しい。多くの応用では、 各データについて平均0、各素子に関して分散0となるように正規化し、ノイズを考慮せずに再構築(注:CD-1法のこと?)を行った後、各素子の分散を1にすることでより簡単に学習させることが出来る。ガウシアン可視素子の再構築された値は2値隠れ素子のtop-down inputプラスそのバイアスの値と一致する。
学習率は、 **2値可視素子を使用した場合と比べ、10倍~100倍小さくする必要がある。**時々報告される失敗についてはおそらく高すぎる学習率を使用したためと思われる。より小さい学習率が求められるのには、再構築においてcomponentのサイズには上界がなく、1つのcomponentが非常に大きくなった場合、そこから生起する重みが非常に大きい学習信号を示すという理由がある。(通常の)2値の可視・隠れ素子においては、各訓練ケースにたいする学習信号は-1から1の間にあるため、バイナリ-バイナリネットはより安定した状態にある。
注:ここで"natural image"という言葉が登場しているが、本記事ではMNISTのような表現が ある程度類似している画像と対比して(現実の写真や動画を始めとした) 多様性のある画像を「自然な」画像と解釈しました。合点の行く説明があったので載せておきます。
Definition of “Natural Images” in the context of machine learning
13.3 ガウシアン可視・隠れ素子
可視素子と隠れ素子両方がガウシアン素子である場合、不安定性による問題はより一層深刻化する。個々の活性は、前提となるノイズレベルを示す標準偏差を持つ2次の"抑制"項の平均の近くに位置するように維持される(The individual activities are held colose to their means by quadratic "containment" terms with coefficients determined by the standard deviations of the assumed noise levels):
E(v,h)=\sum_{i\in\ vis}\frac{(v_i-a_i)^2}{2\sigma_i^2}+\sum_{j\in\ hid}\frac{h_j-b_J}{2\sigma_j^2}-\sum_{i,j}\frac{v_i}{\sigma_i}\frac{h_j}{\sigma_j}w_{ij}
重みベクトルのいずれの固有値も十分に大きくなり、2次の相互作用項は"封じ込め"項を凌駕するようになる。さらには、対応する固有ベクトルの方向に関する活性のスケールアップによって達成されるエネルギーには下界が存在しない。十分に小さい学習率において、CD-1法はこれらの方向を検知し、修正してくれるため、全てガウシアン素子を用いる 因子分析(Marks and Movellan, 2001)の無向版モデルを学習することが可能になる。しかし、これは有向モデルに対しEM法(Ghahramani,and Hinton, 1996)を用いるよりも難しい挑戦となる。
13.4 二項素子
0からNまでのノイジー(noisy)な整数値を取る素子を得る簡単な方法は、別々の2値素子をN個用紙して、いずれの素子にも同じ重みとバイアスを持たせることである(Teh and Hinton, 2001)。すべてのコピーが同じ入力を受け取るため、それらの素子すべてが同じ、活性化確率$p$を持つこととなり、その計算は1回で済む。期待されるONの数は$Np$であり、その分散は$Np(1-p)$となる。小さい$p$に対しては、これはポアソン素子のようにふるまうが、pが近づくにつれ分散はまた小さくなり始める。これは好ましい兆候ではない。また、小さいpに対してはその増加は入力の合計に指数比例する。この性質は次節に紹介する修正線形素子と比べ、学習を不安定にさせる。
重みを共有することで、2値素子から新しいタイプの素子を作ることには1つ良いことがある。それは、背後に存在するバイナリ-バイナリRBMの数学的性質をそっくり引き継いでいることだ。
13.5 修正線形素子
二項素子に対する小さな修正は、現実のニューロンのモデルとして非常に興味深い性質をもたらすと共に、実問題への応用にも適用しやすくする。各コピーは相変わらず同じ学習重みベクトル$w$及びバイアス$b$を持つが、各コピーはバイアスに対してそれぞれ異なる固定のオフセットを持つ。もしオフセットの値が-0.5,-1.5,-2.5,...-(N-0.5)であればこれらのコピーの確率の合計は以下の閉形式に非常に近づく:
\sum_{i=1}^{\infty}\sigma(x-i+0.5)\approx\ log(1+e^x)
このとき、$x=\textbf{vw}^T+b$である。したがって各コピーの活性の合計は十分に大きな入力を与えたときに(線形に)漸近(saturate)する滑らかな修正線形素子のような振る舞いを持つ。$log(1+e^x)$が指数型分布族に属さないにもかかわらず、これは重みを共有する複数の2値ユニットに固定バイアスオフセットを施すことによって正確にモデリングすることができる。このモデルは2値素子モデル以上のパラメータを持たないが、より表現力の高い変数を提供する。分散は$\sigma(x)$であるため、素子たちは堅固にノイズを作らない方向に動きxが大きい際もノイズは大きくならない。
各コピーに対して固定のオフセットを与えることの欠点は、正確に整数値を見積もるための確率の計算において、ロジスティック関数が複数回計算される必要があることである。もっとも、修正線形素子によって見積もられる値が整数値という制約を受けないという条件において、高速な見積もりを使用することは可能である。(ロジスティック関数の代わりに)$max(0,x+N(0,1))(N(0,1)は平均0、分散1のガウス分布を表す)$を使うことで見積もられる。このタイプの修正線形素子は CD-1法においていずれの他の可視素子や隠れ素子よりも上手く動いているように見える。
もし可視素子と隠れ素子双方が修正線形素子であるならば、重みの更新における不安定な運動(dynamics)を避けるためにより小さい学習率が必要になる場合がある。もし2つの修正線形素子の間の重みが1より大きくなった場合、両素子に対して非常に高い活性を与えることによるエネルギーの下界がないため、適切な確率分布を形成することが出来なくなる。それでもやはり、多数の反復を繰り返した場合マルコフ連鎖が吹き飛ぶような学習時間を、十分に方向の検知・修正を行える程度に低い学習率で行った場合、CD法は適切な学習を行ってくれる(Nevertheless, contrastive divergence learning may stil work provided the learning rate is low enough to give the learning time to detect and correct directions in which the Markov chain would blow up if allowed to run for many iterations)。修正線形素子により構成されたRBMはガウシアン素子によって構成されたRBMよりも安定している。なぜなら、修正が、1つのミニバッチに対する非常に大きい正の活性に続き、次のミニバッチで非常に大きい負の値が来ることによる、重みの2相(biphasic)振動を防ぐからである。
14 CD法の派生形
CD-1法は最尤推定において非常に良い近似ではないにも関わらず、より高次のRBMを積み上げるための隠れた特徴を取り出すという目的においては全く問題がない。 CD-1法は(訓練データから1回しかギブスステップを踏まないため)隠れ層の表現はデータベクトルの殆どの情報を維持する。そのため、正確な最尤推定の近似を取り出すために、データベクトルの情報をいくらか失うようなCD法の形を取ることは必ずしも良いとは限らない。とはいえ、良い密度や結合密度を持つRBMを学習させることが主となる目標となるならば、CD-1は選択肢から外れることとなる。
学習の初期段階においては、重みは小さく混合も非常に高速なため、CD-1法は最尤推定の良い近似となる。重みが大きくなるにつれて、混合は悪くなり、CD-n法のnの値を徐々に引き上げていくことが意味を持つようになる。nが増加したとき、学習に用いられる対の統計量の差異?(the difference of pairwise statistics)が増加するため、学習率を下げる必要が出てくるだろう。
CD-1法の学習の初期地点を根本的に変えた方法として**"persistent(持続的、継続的) contrastive divergence"法(PCD法)**(Tieleman, T., 2008)と呼ばれる方法がある。毎回のギブスマルコフ連鎖の初期値にデータ点―これがCD法の本質であるが―を用いる代わりに、我々は持続的連鎖(persistent chain)または"fantasy particles"と呼ばれるものの状態を追う。各持続的連鎖は各重みの更新ごとに自らの可視層及び隠れ層の状態を1回(または数回)更新する。このときの学習信号はデータのミニバッチを用いた対の統計量と、持続的連鎖を用いた際の対の統計量との差異となる。一般に持続的連鎖の数はミニバッチの大きさと同じに設定されることが多いが、これといった根拠はない。この持続的連鎖を用いた混合は驚くほど早い速度で進行する。なぜなら、重みの更新のたびに状態のエネルギーを上昇させるために、現在の連鎖の元の重みを撃退(退ける)ように更新が行われるからだ(局所的な地点に停滞しない)。
PCDを使用する際は、 一般に学習率はかなり小さくする必要があり、学習の初期においてはなかなか再構築誤差が低下しない。学習の初期では持続的連鎖は各連鎖ごとにしばしば強い相関を持つが、これは時間をかけることで解決する。最終的な再構築誤差もしばしばCD-1法に比べて大きい。なぜなら、PCD法は漸近的に、(CD法のように)1回の再構築の分布から本来の分布と似た分布を生成するというより、通常の最尤推定法の学習を進めているからだ。PCD法はCD-1やCD-10と比べても明らかに良いモデルを学習し、最適な密度モデルを生成するという目標においては強く推奨される方法となる。
PCD法は基本となるパラメータに加えて”fast weights"による書き換えを行うことで改善できる。"fast weights"は非常に高速に学習を進めるが同時に高速に減衰する。これらのfast weightsは持続的連鎖の混合をより良くする。しかしながら、fast weightsの導入はより多くの超パラメータが出現することを意味し、本稿ではこれ以上このトピックについては扱わない(Tieleman, T., Hinton, G.E, 2009を見よ)。
15 学習状況の可視化
学習をおかしな方向に進める方法は多く存在し、共通する殆どの問題は適切な図示によって容易に診断することができる。以下に説明する3つの描画法によって、(学習中に)何が起こっているか、単純に再構築誤差をモニタリングするよりも多くの洞察を与えてくれる。
**結合重み及び可視層・隠れ層の各バイアスをヒストグラムにするのは非常に有効だ。**さらには、更新時の彼らの値の変化を調べることはさらに有効だ。もっとも、更新のたびにヒストグラムを作成するのは無駄が多いのだが。
可視層が空間的・時間的構造(have spatial or temporal structure)(例えば、画像や音声)を持つとき、可視層と接続している各隠れ層の重みを図示することは非常に効果的だ。これらの"受容"(receptive)野は隠れ素子が学習した特徴を可視化する良い方法だ。多くの隠れ素子の受容野を可視化する際、各隠れ素子に対して異なるスケールを用いることは、大きな誤解を招くことになりかねない。グレースケールによる図示は地味だが色を用いた図示より多くの示唆を与えてくれる。
単独のミニバッチに対しては、ミニバッチ中の各訓練データに対する、各(2値)隠れ素子の確率を表す[0,1]の範囲の値をグレースケールで図示することは非常に効果的だ(ちなみに、隠れ素子が数百個あるならば、単純にその一部を用いればよい)。これは、全く使われていない隠れ層や、異常に多くの(少数の)隠れ素子を発火させるような訓練データを即座に発見できるようにしてくれる。隠れ素子たちがどれだけ信頼できるかも同時に示してくれる。学習が適切に進んでいる際は、この表示は明らかに垂直あるいは水平な線の見えない、ランダムな表示である必要がある。ヒストグラムをこの図示法と同様に使用することもできるが、同じ学習が行われるまで非常に多くのヒストグラムを図示する必要がある。
16 識別におけるRBM
RBMを識別に用いるには、3つの分かりやすい方法がある。1つ目の方法は、学習済みの隠れ層の出力を入力として、一般的な識別モデルに当てはめることだ。この方法については、本稿ではこれ以上議論しない。もっとも、特に多くの隠れ層が識別モデルの学習の前に教師なしで事前学習されている場合には、この方法がRBMのもっとも重要な利用法になるはずである。
2番目の方法は、各クラスに関して別々のRBMを学習させるという方法だ。学習終了後、テスト用ベクトル$\textbf{t}$の自由エネルギーが各クラス専用のRBMによって計算される(16.1を見よ)。クラスcを用いて学習されたRBMを$\textbf{t}$に対して適用した際の対数尤度は以下で与えられる:
log\ p(\textbf{t}|c)=-F_{c}(\textbf{t})-logZ_{c}
このとき、$Z_c$は該当のRBMの分配関数を表す。各RBMはそれぞれ未知で、異なる分配関数を持つため、自由エネルギーを直接識別のために使うことはできない。しかしながら、クラス数が少なければ、未知の分配関数の対数を、単純に(各訓練データセットにおける)"ソフトマックス"モデルを用いることで処理することは難しくない。これを用いて、各クラスに対応するRBMから得られた自由エネルギーから(テストデータ$\textbf{t}$の)クラスを予測することが出来る:
log\ p(class=c|\textbf{t})=\frac{e^{-F_c(\textbf{t})-log\hat{Z}_c}}{\sum_{d}e^{-F_d(\textbf{t})-log\hat{Z}_d)}}
ここで$\hat{Z}$はソフトマックスの最尤推定学習によって得られたパラメータを表す。勿論、上式は各RBMのバイアスや重みを学習するためにも使えるが、これは過学習の回避に多くのデータ量を必要とする。各重さとバイアスに対する識別勾配?(dicriminative gradients)とCD法による勾配の近似値を組み合わせることで、それらのメソッド単体を用いるよりもしばしば良く学習する。CD法によって生成された勾配の近似値は過学習を防ぐための強い正則化器(regulrizer)として働くため、識別モデルの構築を助けるような重みやバイアスを用いる一定のプレッシャー(pressure)がある。
3つ目の方法は、2セットの可視層を持つ単独のRBMを用いて、結合密度モデルを学習させることだ。データベクトルを表現する素子の層に加えて、クラスを表す"softmax"ラベル素子が与えられる。学習後、各possible labelは順番にテストベクトルによって計算され、最も低い自由エネルギーを与えた1つのラベルが最ももっともらしいクラスとして選ばれる。この場合は、分配関数は問題にならない。なぜなら、全クラスに対して(分配関数は)全く同一であるからだ。再度、正しいクラスの対数尤度の微分である識別勾配を用いることで、結合(joint)RBMの識別的学習(discriminative training)と生成的学習(generative training)を組み合わせることが可能である(Hinton, G.E, 2007):
log\ p(class=c|\textbf{t})=\frac{e^{-F_c(\textbf{t})}}{\sum_{d}e^{-F_d(\textbf{t})}}
16.1 可視ベクトルの自由エネルギーを計算する
可視ベクトル$v$の自由エネルギーis the energy that a single configuration would need to have in order to have the same probability as all of the configurations that contain $v$:
e^{-F(\textbf{v})}=\sum_{h}e^{-E(v,h)}
これは期待されるエネルギーマイナスエントロピーによっても与えられる:
F(v)=-\sum_{i}v_{i}a_{i}-\sum_{j}p_{j}x_{j}+\sum_{j})(p_{j}log\ p_{j}+(1-p_{j})log\ (1-p_{j}))
ここで、$x_j=g_j+\sum_i v_{i}w_{ij}$は隠れ素子$j$に対する入力の合計を表し、$p_j=\sigma(x_j)$は$v$が与えられたとき$h_j=1$となる確率を表す。$F(v)$を計算する良い方法として、さらに自由エネルギーの別の表現を用いる方法がある:
F(v)=-\sum_{i}v_{i}a_{i}-\sum_{j}log\ (1+e^{x_j})
17 欠損値を処理する
有向(directed) belief netにおいては、可視層の欠損値を処理することは非常に簡単だ。推論を行う際、有向の矢印の終点(有向の矢印の始点にある発信側に影響を与えない)に欠損データがあるからだ。しかしこれは無向結合を持つRBMにおいては正しくない。標準的な方法で推論を行うためには、欠損値は(代わりの値で)埋められる必要があり、それには少なくとも2つの方法がある。
欠損値のとりわけ基本的な形は、各訓練ケースが画像プラス単独の離散ラベルで構成されたベクトル$v$で構成されているデータの結合密度を学習するときに発生する。もし各ケースの部分集合のラベルが失われていれば、それ(欠損ラベル)はそれの正確な条件付き分布からギブスサンプリングされる。これはそれぞれの可能なラベルの自由エネルギーを計算し(16.1を見よ)、$exp(-F(l,v))$に比例する確率によってラベル$l$を決定することによって実現できる。この過程を経て、訓練ケースはあたかも完全な(欠損値のない)訓練ケースのように扱われる。
連続値の可視素子に対しては、たとえ複数の欠損値が存在していても同様に動くような、異なる欠損値の補完法が存在する。訓練データにおける学習サイクルを多くの回数繰り返すとき、欠損値は重みの学習と同時に更新される。しかしおそらく学習率には異なる値が用いられるだろう。訓練ケース$c$における隠れ素子$i$の欠損値の更新は:
\delta v_{i}^{c}=\epsilon(\frac{\partial F}{\partial \hat{v}_{i}^{c}}-\frac{\partial F}{\partial v_{i}^{c}})
ここで、$v_{i}^{c}$は補完(imputed)値であり、$\hat{v}_{i}^{c}$は補完値の再構築値である。補完値においても、他のパラメータと同様にモーメンタムを用いることができる。
欠損値の数が非常に多い場合であっても、欠損値を処理できるより抜本的な方法が存在する。This occurs, for example, with user preference data where most users do not express their preference for most objects。欠損値を補完する代わりに、異なる訓練ケースに対して異なる可視素子を持つRBMを使ってその欠損値が存在しないと見なす。異なるRBMたちは重みを共有する別々の族モデルを構成する。各族のRBMは今やその隠れ層に対して正しい推論を行うことが出来るようになるが、重みの共有は特定のRBMに対して理想的でないということを意味する。欠損値に対して可視素子を追加し、欠損値を積分消去するように確かな推論を行うことは、単純に可視素子を取り除いた場合と同じ隠れ層の分布を与えない。なぜなら、それ(後者?)はモデルの族であって、単独のモデルではないからだ。欠損値に対してモデルの族を使う際は、RBM内によって隠れ層のバイアスを可視層の素子数によってスケールすることは非常に有用である。
謝辞:本研究はNSERC及びCanadian Institute for Advanced Researchによって支援された。私の過去及び現在の多くの院生及びポスドク達は本論文で述べた実践的な知識の内容に関して貴重な貢献をしてくれた。私は貴重な各貢献に対してそれぞれ感謝の意を示そうとしたが、誰が何を提案してくれたか必ずしも思い出すことはできなかった。
サマリー
ここまで淡々と訳してきましたが、最終的にまとめるならば次のようになるでしょう。
比較的具体的な基準のあるものが多いです。
◆是非使いたい
3.1 隠れ層の更新…データ項の更新は離散値、再構築項の更新には連続値を用いる
3.2 可視層の更新…データ項、再構築項共に連続値を用いる
4.1 ミニバッチの大きさ:
クラス数が小さい場合:クラス数と同じ数
クラス数が多い場合:10個程度
5.1 再構築誤差の可視化
「使用はするが、信用してはいけない」。正確に何が起こっているか把握するには、ALSのような尤度推定や、その他の可視化法を用いること。
6.1 過学習のモニタリング
平均自由エネルギーを計算して、訓練データと検証データを入れた際の値の動きを見る。
7.1 学習率
まずは重みの更新量と重みそのものの変化を見ることが第一。重みの更新量は重みそのものの$10^{-3}$倍が一般に望ましい。
8.1 重み($w_{ij}$)とバイアス($b_i,c_j$)の初期値
重み$W_{ij}$:N(0, 0.01)からランダムに初期化すればよい。
可視層バイアス$b_i:log[p_i/(1−p_i)]$($p_i$は訓練データのうち素子iがON(1)になっているデータ点の比率とする)
隠れ層バイアス$c_j$:初期化の方法よりも、隠れ素子が常に0か1になっていないか頻繁にチェックすることが重要
10.1 荷重減衰
重みのペナルティとして0.00001をまず試してみる。
12.1 隠れ素子の数
データベクトルの持つ情報量を基準に設定する。データ量が十分に多く、画像のクラス分類のようにデータの表現量が枚数に対して落ちる場合にはそれを考慮する必要がある。
15 学習状況の可視化
再構築誤差の評価だけでは分からない時、以下の3つの方法を使おう。
①重み及びバイアスのヒストグラムによる可視化
②可視素子に対する隠れ層の重さのグレースケールによる図示
③各訓練データに対する、各隠れ素子の確率を用いたグレースケールによる図示(要は、RBMに入力を入れたときの出力)
◆性能を上げるなら
9.1 モーメンタム
学習の初期で0.5、誤差の減少が落ち着いたら0.9。学習させるデータの性質次第で学習の速度が大幅に上昇する。
11.1 スパース化目標
スパース化目標を0.1~1、減衰件数を0.9~0.99に設定。一般にスパースにすると学習性能が上がるので、面倒でなければ取り入れたい。
◆必要に応じて
13 2値素子以外の様々な素子
現実世界の画像や、音声データに対しては、2値素子では十分な性能が出ない可能性がある。その場合は、ガウシアン可視素子や修正線形素子の利用を検討する。
14 CD法の派生形
PCD法はRBM単独の最適な学習法としては向いているが、多段に重ねてよりよい性能を出すという観点から見るとやや違う節がある。使用には検討が必要。
17 欠損値の処理
欠損値を補完するアプローチと、欠損値を省いたRBMを複数用意して後で統合する方法がある。本稿で扱った内容では不十分かもしれない。
その他の期待できそうなGood Parts
- Dropout
勾配法でパラメータを更新する最中に、ランダムに結合の一部の 素子を選び出し、その素子とつながっている結合を全て取り除く(パラメータを0にする)ことで、、過学習を抑制します。大方の合意として、 50%程度削ると良いとされています。DeepなNetworkの部品の1つとしてRBMを考えた場合、RBMの「可視層と隠れ層すべてに対して結合がある」という性質は、表現力を上げると同時に ある入力の変化に対し、多くのユニットが影響を受けてしまう現象が起こります。これをあえて半分というかなり多くの結合を切ることによって、素子同士の関係がやや疎(Sparse)になって、結果として多少の入力では出力がゆらがない汎用的な出力が出来ると考えられます。
画像処理の分野で有名なCNN(Convolutional Neural Network)も近くのノードとしか結合を取らないようなネットワーク構造をしており、CNNとDropoutの効果は同種のものなのではないかと思います。とりあえず試すとよいです。
- DropConnect
Dropoutと混同しやすいですが、今度は素子を選ぶのではなく、 結合そのものをランダムに選び出してパラメータを0にします。Dropoutの一般化とも言えます。調査不足でポテンシャルは評価しかねています。すみません。
-
画像の平均化
これも有名な方法です。データセットの中には、明るい画像・暗い画像・色の分布の偏った画像が存在します。そこで、データを入力する前に必ず画像のピクセル値の平均及び分散を同じ値にするような処理を与えます。そうすることで、画像そのものの特徴(相対的な偏り)に注目して学習・分類が出来るようになります。なぜそれが効果的なのかは今回は扱えませんでしたが、まずやっておいて良いと思われます。 -
CSL(conservative sampling-based log-likelihood) estimator
今回個人的に気になったトピックです。DBNのような複雑な構造のモデル(特に生成モデル)では、対数尤度の正確な計算が解析的に不可能な事例があります。とはいえ、対数尤度はRBMのようなモデルの「性能」を表す重要な数値の1つであるため、その計算をサンプリングを用いて計算する需要があります。今までは、ALS(Annealed Importance Sampling) estimator(Neal, 2001)という指標が用いられていたのですが、それに代わる指標として登場したようです。
特徴として、少ないサンプルで対数尤度を見積もることが出来るのは勿論のこととして、RBMに組み込まれているサンプリング手法の設定による変化にも追従できるということが挙げられています。この辺りの注目度はあまり高くはありませんが、モデルの学習状況を追う際に使えるのではないかと考えています。
詳細は
Bengio, Y., & Yao, L. (2014). Bounding the test log-likelihood of generative models. arXiv preprint arXiv:1311.6184.
を参照してください。
実践に役立ちそうな情報を書いているスライド
Hintonに並ぶDLの研究者であるBengioによるPractical Recommendations for Gradient-Based Training of Deep Architectures(Y. Bengio, 2012)の解説です。今回紹介した論文より広い範囲に言及しています。
32x32 pixelの大きさの小さな画像が多数揃ったデータセットを使って、今回紹介した様々な手法の有無や、パラメータの値によってどのように結果が変わるか紹介してらっしゃいます。データセットが軽量なので手元でもできる程度の処理量で済むようです。
エンジニアはどの程度まで理論を知っておくべき?
正直、機械学習やそれに関連するアルゴリズムを短期間で理解するのには 無理があります。特に、Deep Learningではそのパラメータの挙動や出力結果を1つ1つ説明することは困難を極めます。そのため、既に用意されているチュートリアルをなぞってそれを改良する、というステップを取るのは致し方ないのではないかと思っています。しかしながら、ブラックボックスの状態でチューニングするのはモデル改善のアプローチとしてもエンジニア本人の心境としても厳しいものがあります。
私の私見ですが、各種機械学習のアルゴリズムや、性能を上げるメソッドを試してみる・勉強してみる際には、 チュートリアルにあるようなシンプルな実装から始めた上、
①そのアルゴリズム・メソッドがどのような問題を解決するために設計されたかを知る
②自分の解決したい問題のデータを適用してみて、各種可視化のメソッドを使ってモデルの学習の挙動を見る
③学習の過程でどのような現象が起きているのか(過学習・正則化・etc)把握し、自分のストックを増やす
というステップを経て、徐々に各アルゴリズムに対する知見を深めていくとよいと思います。数式的な理解や、背後にある数学的理論は、時間のある時に1年ほどかけて勉強すればよいと思います(勿論、勾配法程度の最適化手法に関する基礎知識は知っておいても良いかもしれません)。
少なくとも機械学習を問題に適用するのに必要なのは、 なぜ学習できるのかではなく、**学習させた際に何が起こるか**の理解です。現象が分かれば、おのずと解決の方向性も見えてくることでしょう。
基本的に、どの機械学習のアルゴリズムも、 与えられたデータ点(+ラベル)に最も良く適合するような確率分布(関数)を学習するということを行っているだけなのですが、面白いことに、アルゴリズムごとに得意不得意があります。これは、 データの特性とモデルの表現力の相性によるものです。もし最初に試してみた方法で上手くいかなければ、その方法に固執する前にその他のアルゴリズムが適用できないか考えてみましょう。
まとめ
- Deep Learningの性能を発揮させるには、モデルに合わせてパラメータや関数を大量に調整する必要がある。ライブラリでは調整しきれない部分も数多く存在する。
- Deep Learningは魔法の杖ではない。利用者がデータの構造を見極めて適切な層の数や形を設定する必要がある。多くても少なくてもいけない。
- 単純な回帰問題やニューラルネットワーク、SVMなどとは対照的に、Deep Learningにおける学習状況の可視化は非常に難しくなる。特にRBMを用いたネットワークでは正しく学習が進行しているか、学習終了のタイミングを間違えていないか、様々な情報を用いて慎重に判断する必要がある。
- なぜ学習できるのか考えるより、学習の過程で何が起きているのか、どう対処すればよいのかを知ることが重要
プログラムを書いて実装をするつもりで始めたのに、結局その前段階に関する長ーい記事になってしまいました。どうしてこうなった。コードを書く以前の環境構築の難易度が高すぎるのが1つの障壁であるような気がします。次こそは実装を書きたい…
用語集
generative model...生成モデル
maximum likelihood learning...最尤学習
weights...重み
bias...バイアス(偏差)
meta-parameter...超パラメータ
stochastic...確率的
Robust...頑健
binary...2値
deterministic...決定論的
training data...訓練データ
validation data...検証データ
test data...テストデータ
GD(Gradient Descent)...勾配法
SGD(Stochastic Gradient Descent)...確率的勾配法
overfitting...過学習
approximate...近似
standard deviation...標準偏差
momentum...はずみ、運動量、今回の場合はGD中に振動の抑制項として使われる
ravine...峡谷、谷
brute-force...力ずく
weight decay...荷重減衰
mixing rate...混合率(理想分布への収束スピード)
coefficient...係数
partition function...分配関数
sparsity target...スパース化目標
sparsity cost...スパース化コスト
stability...安定性
discriminative...識別の
order of magnitude...10の累乗
eigenvalue...固有値
eigenvector...固有ベクトル
natural image...自然イメージ、多様性のあるイメージ
rectified...修正された
exponential family...指数型分布族
integrate out...積分消去
参考資料
スライドなど
Practical recommendations for gradient-based training of deep architectures 日本語解説
MIRU2014 tutorial deeplearning
【翻訳】効果的なディープラーニング(深層学習)モデルのための10のヒント
Deep Learning 実装の基礎と実践(得居誠也)
Deep Learning 技術の今(得居誠也)
Learning Deep Architectures for AI 日本語解説
RBM and sparsity penalty
論文
Hinton, G. E. (2012). A practical guide to training restricted boltzmann machines. In Neural Networks: Tricks of the Trade (pp. 599-619). Springer Berlin Heidelberg.
Hinton, G. (2010). A practical guide to training restricted Boltzmann machines. Momentum, 9(1), 926.
↑2バージョンあります。基本的な内容は変わっていません。
Bengio, Y. (2012). Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of the Trade (pp. 437-478). Springer Berlin Heidelberg.
Bengio, Y., & Yao, L. (2014). Bounding the test log-likelihood of generative models. arXiv preprint arXiv:1311.6184.
Fischer, A., & Igel, C. (2012). An introduction to restricted Boltzmann machines. In Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications (pp. 14-36). Springer Berlin Heidelberg.
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., & Salakhutdinov, R. R. (2012). Improving neural networks by preventing co-adaptation of feature detectors. arXiv preprint arXiv:1207.0580.
Wan, L., Zeiler, M., Zhang, S., Cun, Y. L., & Fergus, R. (2013). Regularization of neural networks using dropconnect. In Proceedings of the 30th International Conference on Machine Learning (ICML-13) (pp. 1058-1066).
Bengio, Y., & Yao, L. (2014). Bounding the test log-likelihood of generative models. arXiv preprint arXiv:1311.6184.