粒子群最適化法(PSO)で関数の最小値を求める

#概要
粒子群最適化法(PSO, Particle Swarm Optimization)とは, 動物の群れの行動をヒントとした群知能の一種です.
この記事では, 粒子群最適化法の簡単な例を紹介します.

#放物面の式
放物面の式は以下のような形で与えられます.

\begin{aligned}
z = x^2+y^2
\end{aligned}

当たり前ですが, 最小値は$(x, y)=(0, 0)$のときに$z=0$となります.
これを粒子群最適化法を用いて求めます.

#粒子群最適化法の解説
以下の記事を参照してください.(§2の添字が一部間違っている?)
粒子群最適化と非線形システム

この記事の§2を実装してみます.
#ソースコード

main.py

# -*- coding: utf-8 -*-

import numpy as np
import random

#評価関数: z = x^2 + y^2
def criterion(x, y):
    z = x * x + y * y
    return z

#粒子の位置の更新を行う関数
def update_position(x, y, vx, vy):
    new_x = x + vx
    new_y = y + vy
    return new_x, new_y

#粒子の速度の更新を行う関数
def update_velocity(x, y, vx, vy, p, g, w=0.5, ro_max=0.14):
    #パラメーターroはランダムに与える
    ro1 = random.uniform(0, ro_max)
    ro2 = random.uniform(0, ro_max)
    #粒子速度の更新を行う
    new_vx = w * vx + ro1 * (p["x"] - x) + ro2 * (g["x"] - x)
    new_vy = w * vy + ro1 * (p["y"] - y) + ro2 * (g["y"] - y)
    return new_vx, new_vy


def main():
    N = 100  #粒子の数
    x_min, x_max = -5, 5
    y_min, y_max = -5, 5
    #粒子位置, 速度, パーソナルベスト, グローバルベストの初期化を行う
    ps = [{"x": random.uniform(x_min, x_max), 
        "y": random.uniform(y_min, y_max)} for i in range(N)]
    vs = [{"x": 0.0, "y": 0.0} for i in range(N)]
    personal_best_positions = list(ps)
    personal_best_scores = [criterion(p["x"], p["y"]) for p in ps]
    best_particle = np.argmin(personal_best_scores)
    global_best_position = personal_best_positions[best_particle]
    
    T = 30  #制限時間(ループの回数)
    for t in range(T):
        for n in range(N):
            x, y = ps[n]["x"], ps[n]["y"]
            vx, vy = vs[n]["x"], vs[n]["y"]
            p = personal_best_positions[n]
            #粒子の位置の更新を行う
            new_x, new_y = update_position(x, y, vx, vy)
            ps[n] = {"x": new_x, "y": new_y}
            #粒子の速度の更新を行う
            new_vx, new_vy = update_velocity(
                new_x, new_y, vx, vy, p, global_best_position)
            vs[n] = {"x": new_vx, "y": new_vy}
            #評価値を求め, パーソナルベストの更新を行う
            score = criterion(new_x, new_y)
            if score < personal_best_scores[n]:
                personal_best_scores[n] = score
                personal_best_positions[n] = {"x": new_x, "y": new_y}
        #グローバルベストの更新を行う
        best_particle = np.argmin(personal_best_scores)
        global_best_position = personal_best_positions[best_particle]
    #最適解
    print(global_best_position)
    print(min(personal_best_scores))

if __name__ == '__main__':
    main()

#結果

結果

{'y': 0.00390598718159734, 'x': -0.0018420875049243782}
1.86500222386e-05

##可視化
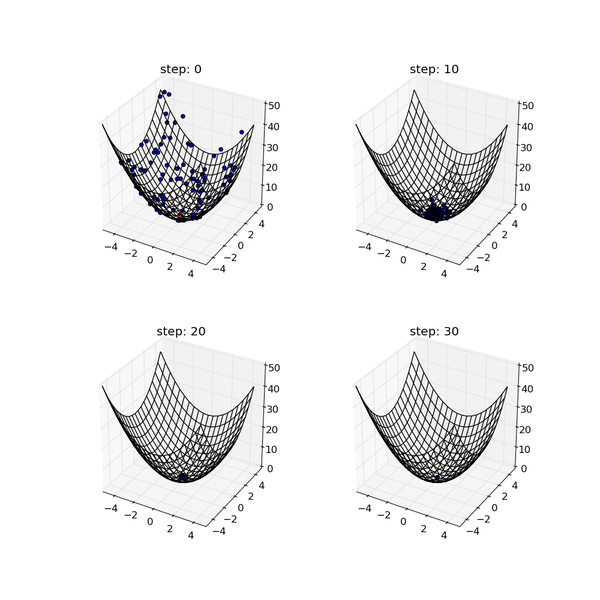
$N(=100)$個の粒子が$(x, y)=(0, 0)$に集中していく様子です.

#その他
粒子の数などのいくつかのパラメータはどうやって決めるんですかね.(Trial and Error?)

---

文献によって位置の更新, 速度の更新, パーソナルベスト, グローバルベストの順序がバラバラ…
この記事では位置の更新⇒速度の更新⇒パーソナルベストの更新⇒グローバルベストの更新で行っています.

#編集履歴

• (2014/11/18)ソースコードの修正