ニューラルネットワークの順伝播，逆伝播，確率的勾配降下法を手計算する

この記事は何？

ニューラルネットワークの理解が曖昧な部分があったので，実際にニューラルネットワークの動きを手計算して確かめた時のメモです．

ニューラルネットワークの構造

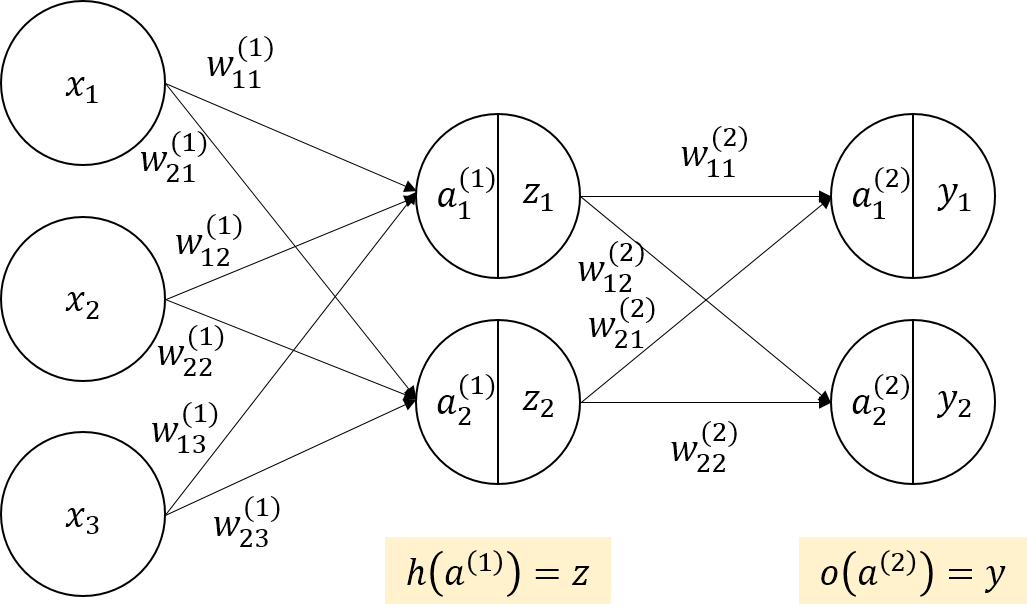
下のような図で表される，小さめの構造のニューラルネットワークの動きを手計算で確かめてみようと思います．
入力層ユニット数は3，隠れ層ユニット数は2，出力層ユニット数は2とします．
隠れ層の活性化関数$h$はシグモイド関数$h(a)=\frac{1}{1+\exp(-a)}$を用います．
出力層の活性化関数$o$は恒等関数$o(a)=a$を用います．

重みの初期値は以下のように設定します．

W^{(1)}=\begin{bmatrix}
w_{11}^{(1)}&w_{12}^{(1)}&w_{13}^{(1)}\\
w_{21}^{(1)}&w_{22}^{(1)}&w_{23}^{(1)}
\end{bmatrix}
=\begin{bmatrix}
0.1&0.1&0.1\\
0.2&0.2&0.2
\end{bmatrix}

W^{(2)}=\begin{bmatrix}
w_{11}^{(2)}&w_{12}^{(2)}\\
w_{21}^{(2)}&w_{22}^{(2)}
\end{bmatrix}
=\begin{bmatrix}
1&2\\
3&4
\end{bmatrix}

数式表現

今回扱うニューラルネットワークの構造を数式に落とします．

a_i^{(1)}=w_{i1}^{(1)}x_1+w_{i2}^{(1)}x_2+w_{i3}^{(1)}x_3\\
z_i=h(a_i^{(1)})=\frac{1}{1+\exp{(-a_i^{(1)}})}\\
a_i^{(2)}=w_{i1}^{(2)}z_1+w_{i2}^{(2)}z_2\\
y_i=o(a_i^{(2)})=a_i^{(2)}

順伝播

訓練データ$({\bf x},{\bf t})$が以下のように与えられているとします．

{\bf x}=(x_1, x_2, x_3)=(1,2,3)\\{\bf t}=(t_1, t_2)=(0,1)

${\bf x}$を入力したときの出力${\bf y}$を求めてみます．

\begin{eqnarray}
a_1^{(1)}&=&w_{11}^{(1)}x_1+w_{12}^{(1)}x_2+w_{13}^{(1)}x_3\\
&=&0.1\cdot1+0.1\cdot2+0.1\cdot3\\
&=&0.6\\
a_2^{(1)}&=&w_{21}^{(1)}x_1+w_{22}^{(1)}x_2+w_{23}^{(1)}x_3\\
&=&0.2\cdot1+0.2\cdot2+0.2\cdot3\\
&=&1.2\\
z_1&=&h(a_1^{(1)})=\frac{1}{1+\exp(-0.6)}\approx0.6457\\
z_2&=&h(a_2^{(1)})=\frac{1}{1+\exp(-1.2)}\approx0.7685\\
a_1^{(2)}&=&w_{11}^{(2)}z_1+w_{12}^{(2)}z_2=1\cdot0.6457+2\cdot0.7685\approx2.183\\
a_2^{(2)}&=&w_{21}^{(2)}z_1+w_{22}^{(2)}z_2=3\cdot0.6457+4\cdot0.7685\approx5.011\\
y_1&=&o(a_1^{(2)})=a_1^{(2)}=2.183\\
y_2&=&o(a_2^{(2)})=a_2^{(2)}=5.011
\end{eqnarray}

というわけで${\bf y}=(2.183,5.011)$が得られました．

逆伝播

順伝播の計算が終わったので，次は誤差逆伝播を手計算してみます．
誤差関数は二乗和誤差$E({\bf y},{\bf t})=\frac{1}{2}\sum_k{(y_k-t_k)^2}$を使います．
まず，各重みの勾配を示します．

\begin{eqnarray}
\delta_i^{(2)}&=&y_i-t_i\\
\frac{\partial E}{\partial w_{ij}^{(2)}}&=&\delta_i^{(2)}z_j\\
\frac{\partial E}{\partial w_{ij}^{(1)}}&=&\frac{\partial E}{\partial a_i^{(1)}}\cdot\frac{\partial a_i^{(1)}}{\partial w_{ij}^{(1)}}\\
&=&(\frac{\partial E}{\partial a_1^{(2)}}\cdot\frac{\partial a_1^{(2)}}{\partial a_{i}^{(1)}}+\frac{\partial E}{\partial a_2^{(2)}}\cdot\frac{\partial a_2^{(2)}}{\partial a_{i}^{(1)}})\cdot x_j\\
&=&h'(a_i^{(1)})(w_{1i}^{(2)}\delta_1^{(2)}+w_{2i}^{(2)}\delta_2^{(2)})\cdot x_j
\end{eqnarray}

それでは，手計算で各重みの勾配を求めてみます．
まずは出力層の誤差を求めておきます．

\begin{eqnarray}
\delta_1^{(2)}&=&y_1-t_1=2.183-0=2.183\\
\delta_2^{(2)}&=&y_2-t_2=5.011-1=4.011
\end{eqnarray}

次に$W^{(2)}$の勾配を求めます．

\begin{eqnarray}
\frac{\partial E}{\partial w_{11}^{(2)}}&=&\delta_1^{(2)}z_1=2.183\cdot0.6457\approx1.410\\
\frac{\partial E}{\partial w_{12}^{(2)}}&=&\delta_1^{(2)}z_2=2.183\cdot0.7685\approx1.677\\
\frac{\partial E}{\partial w_{21}^{(2)}}&=&\delta_2^{(2)}z_1=4.011\cdot0.6457\approx2.590\\
\frac{\partial E}{\partial w_{22}^{(2)}}&=&\delta_2^{(2)}z_2=4.011\cdot0.7685\approx3.083\\
\end{eqnarray}

次に$W^{(1)}$の勾配を求めます．

\begin{eqnarray}
\frac{\partial E}{\partial w_{11}^{(1)}}&=&h'(a_1^{(1)})(w_{11}^{(2)}\delta_1^{(2)}+w_{21}^{(2)}\delta_2^{(2)})\cdot x_1\\
&\approx&0.2288\cdot(1\cdot2.183+3\cdot4.011)\cdot1\\
&\approx&3.252
\end{eqnarray}

えっこれあと5回もやるの……辛すぎる～～～ってなったので，逆伝播はこれでお終いにします．

確率的勾配降下法による学習

以下の式を用いて重みを更新します．学習率$\eta$は0.1としました．

w\leftarrow w-\eta \frac{\partial E}{\partial w}

まずは$W^{(2)}$を更新します．

\begin{eqnarray}
w_{11}^{(2)}&\leftarrow& w_{11}^{(2)}-\eta \frac{\partial E}{\partial w_{11}^{(2)}}=1 - 0.1\cdot 1.410\approx0.8590\\
w_{12}^{(2)}&\leftarrow& w_{12}^{(2)}-\eta \frac{\partial E}{\partial w_{12}^{(2)}}=2 - 0.1\cdot 1.677\approx1.832\\
w_{21}^{(2)}&\leftarrow& w_{21}^{(2)}-\eta \frac{\partial E}{\partial w_{21}^{(2)}}=3 - 0.1\cdot 2.590\approx2.741\\
w_{22}^{(2)}&\leftarrow& w_{22}^{(2)}-\eta \frac{\partial E}{\partial w_{22}^{(2)}}=4 - 0.1\cdot 3.083\approx3.692\\
\end{eqnarray}

次に$W^{(1)}$を更新します．さっきサボってしまったので，$w_{11}^{(1)}$だけ更新します．

w_{11}^{(1)}\leftarrow w_{11}^{(1)}-\eta \frac{\partial E}{\partial w_{11}^{(1)}}=0.1 - 0.1\cdot 3.252\approx -0.225

答え合わせ

今までやってきたことをChainerで実装し，答え合わせをしました．
Chainerで実装されているmean_squared_error関数は$\frac{1}{2}$を掛け算しない実装なので，自前で二乗損失関数を実装しました．

import numpy as np
from chainer import Function, Variable, optimizers
from chainer import Chain
import chainer.functions as F
import chainer.links as L


class NN(Chain):

    def __init__(self):
        initial_W1 = np.array([[.1, .1, .1], [.2, .2, .2]], dtype=np.float32)
        initial_W2 = np.array([[1, 2], [3, 4]], dtype=np.float32)
        super(NN, self).__init__(
            l1=L.Linear(3, 2, nobias=True, initialW=initial_W1),
            l2=L.Linear(2, 2, nobias=True, initialW=initial_W2)
        )

    def __call__(self, x):
        a_1 = self.l1(x)
        print("a_1\n{}".format(a_1.data))
        z = F.sigmoid(a_1)
        print("z\n{}".format(z.data))
        a_2 = self.l2(z)
        print("a_2\n{}".format(a_2.data))
        y = a_2
        print("y\n{}".format(y.data))
        return y


class SquaredError(Function):

    def forward(self, inputs):
        x0, x1 = inputs
        self.diff = x0 - x1
        diff = self.diff.ravel()
        return np.array(diff.dot(diff) / 2.),

    def backward(self, inputs, gy):
        gx0 = self.diff
        return gx0, -gx0


def squared_error(x0, x1):
    return SquaredError()(x0, x1)

if __name__ == '__main__':
    nn = NN()
    x = Variable(np.array([[1, 2, 3]], dtype=np.float32))
    t = Variable(np.array([[0, 1]], dtype=np.float32))
    y = nn(x)
    optimizer = optimizers.SGD(lr=0.1)
    optimizer.setup(nn)
    nn.zerograds()
    loss = squared_error(y, t)
    loss.backward()
    print("loss\n{}".format(loss.data))
    print("W^1 grad\n{}".format(nn.l1.W.grad))
    print("W^2 grad\n{}".format(nn.l2.W.grad))
    print("before W^1\n{}".format(nn.l1.W.data))
    print("before W^2\n{}".format(nn.l2.W.data))
    optimizer.update()
    print("after W^1\n{}".format(nn.l1.W.data))
    print("after W^2\n{}".format(nn.l2.W.data))

実行結果です．手計算が合ってることを確かめることができました．

a_1
[[ 0.60000002  1.20000005]]
z
[[ 0.64565629  0.76852483]]
a_2
[[ 2.18270588  5.01106834]]
y
[[ 2.18270588  5.01106834]]
loss
10.426437377929688
W^1 grad
[[  3.25237656   6.50475311   9.75712967]
 [  3.63076901   7.26153803  10.89230728]]
W^2 grad
[[ 1.4092778   1.67746365]
 [ 2.58977151  3.0826056 ]]
before W^1
[[ 0.1  0.1  0.1]
 [ 0.2  0.2  0.2]]
before W^2
[[ 1.  2.]
 [ 3.  4.]]
after W^1
[[-0.22523767 -0.5504753  -0.87571293]
 [-0.16307689 -0.5261538  -0.88923079]]
after W^2
[[ 0.85907221  1.83225369]
 [ 2.74102283  3.69173956]]

その他

なかなかメンドウですね…ですが，分かりにくいものは実際に手を動かしてみないと理解しづらいんじゃないかなあ．
隠れ層がもっと増えたら，もう少し誤差逆伝播してる感が出るのかなと思います．