(本稿は, システム系論文紹介 Advent Calendar 2014, 12/20 です http://www.adventar.org/calendars/440)
論文は arXiv から取得できます.
http://arxiv.org/abs/1406.2294
Jump Consitent Hash と呼ばれる, 分散ストレージ系で有益なハッシュ関数を求めるアルゴリズムです. 現在史上最強のハッシュアルゴリズムのひとつと言えるでしょう. 無性に分散ストレージライブラリを作りたくなってきますね!
共著者の Eric Veach にも注目です. Google を救ったと言われている distinguished engineer です.
(G 社のひとは彼の名前を社員名簿データベース? から探してみましょう! 社員番号 20 くらいにあるらしいですよ!)
そんな彼がなんと 10 年以上ぶりに論文を出していますので, これはもう読んで紹介するしかない.
コードは 5 行!
int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
int64_t b = 1, j = 0;
while (j < num_buckets) {
b=j;
key = key * 2862933555777941757ULL + 1;
j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
}
return b;
}
なんともシンプルですね! いろいろ紐解いていきましょう.
Consistent hash
さて, そのまえに consistent hash についておさらいします.
たとえば, 最初にバケット(bucket)が 10 個あり, hash(key) % 10 で bucket ID を算出して, データアイテムをそれぞれの bucket に保持していたとしてます. その後, バケット数を 12 個に拡張したとします.
通常のハッシュ関数では hash(key) % 10 != hash(key) % 12 ですから, データアイテム(key)に対して新しいハッシュを求めると, 再計算されたバケット番号が異なるために, バケット間でのデータの移動が発生してしまいます.
たとえば個々のバケットがインターネット越しに存在していると考えてみましょう. バケット(たとえば DB でいうシャードノード)を追加するたびに, たくさんのデータをネット越しに移動してリバランスしなくてはならないとなると, つらくて涙で枕を濡らす日々になってしますね...
理想としては最初の 10 個のバケットにあった 1/6 のデータのみが, 新しい 2 個のバケットに移動し(1/6 = 12/(12-10)), 残りは元々のバケット番号の場所にとどまってほしいですね. つまり, 5/6 のキーに対して hash(key) % 10 == hash(key) % 12.
このような特性が出るようなハッシュアルゴリズムは, consistent hash と呼ばれています(http://en.wikipedia.org/wiki/Consistent_hashing). consistent hash アルゴリズムとしては, Karger et al. が有名なようです(Akamai の Web キャッシングに使われている?).
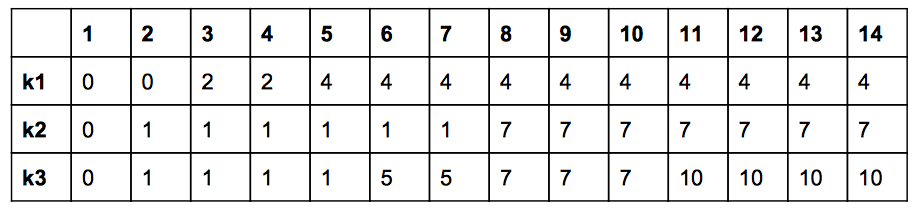
consistent hash による bucket ID の割り当て例を示します.
横軸の数字が bucket 数 です. 縦軸がキー(k1, k2, k3 の三種類)になります. cell 内が bucket ID になります. どれも, bucket ID は, 0 から始まり右にいくほど(bucket が増えていくほど) increasing して, かつ bucket 数より小さいことが見て取れますね.
Jump consistent hash
上記のようなテーブル表にあるような bucket ID 割り当ての性質を持つ, jump consistent hash とは以下のようになります.
(ch() = consistent hash の略です)
int ch(int key, int num_buckets) {
random.seed(key);
intb=0; // This will track ch(key,j+1).
for (int j = 1; j < num_buckets; j++) {
if (random.next() < 1.0 / (j + 1)) b = j;
}
return b;
}
キーはなにかしらの方法で int 値に変換されているものとします. キーの値を乱数のシードとして設定し, 乱数をドロー(draw)して, 確率的に bucket ID を決めて行きます.
バケット数が 2 のケースを考えて見ましょう.
j = 1 のとき, random.next() < (1/2) となりますから, キーは半分の確率で bucket 0 にとどまり, 半分の確率で bucket 1 に移行します. 乱数が十分に偏りがなければ, これは任意のキーに対して, bucket ID 0 と 1 が, 等しく分布して出力されるのが自明ですね.
バケット数が 3 のとき,
j = 1 : (1/2) の確率で j にジャンプ
j = 2 : (1/3) の確率で j にジャンプ
になります. これを一般化して n までとなると, なんとなく与えられた [0, n) の中で, 任意のキー値に対して等しく bucket ID が分布しそうなのが想像できますね. より詳細な数学は論文をぜひ読み解いてみてください.
探索を高速化する.
しかし, 今のままでは, bucket ID を求めるところがリニアサーチになっているので, buckets が 10 万とか 100 万とかになると計算時間もそれなりにかかってしまいます.
そこで, いろいろジャンプの性質を解析すると, あら素敵, 探索を log 時間で行うことができるようになります(より詳細は論文をぜひ読み解いてください)
int ch(int key, int num_buckets) {
random.seed(key);
int b = 1; // bucket number before the previous jump
int j = 0; // bucket number before the current jump
while (j < num_buckets) {
b=j;
r = random.next();
j = floor((b + 1) / r);
}
return = b;
}
ここで重要なのは, jump consistent hash では 記憶領域を使っていない ことです.
既存研究では, 記憶領域(メモリ)を使って木構造を作るなどしてうまくハッシュ値の出力のバランスを取りつつも探索を高速化する方法はありました. しかし, メモリを消費する場合, bucket の数が増えるとメモリ消費が多くなり, かつハッシュの計算時にキャッシュミスが起こり, ハッシュ計算の性能が低下するという問題がありました.
提案手法では, そのような問題がありません.
Simplify する.
さて, ここで random(疑似乱数)は, 生成される疑似乱数の質がよければ基本的にはどのようなアルゴリズムでもよいことがわかります.
そこで論文では, Linear Congruential Generator(LCG) による高速かつ質のよい擬似乱数アルゴリズムを使っています.
(Cite されている Pierre L'Ecuyer 先生も, とっても有名ですのよ! http://www.iro.umontreal.ca/~lecuyer/)
これにより, 最終的にコードは最初に示した結果になります.
int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
int64_t b = 1, j = 0;
while (j < num_buckets) {
b=j;
key = key * 2862933555777941757ULL + 1;
j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
}
return b;
}
Cool!
性能
Jump Consistent Hash では乱数と確率の性質を使って記憶領域を使わずとも, 高速で(log オーダー), かつ分布のよいハッシュ値計算を実現しています.
論文を見ますと, 分布の質もよく, かつ高速に計算できていることが見て取れます.
アルゴリズムを可視化して理解を深める.
ナウなヤングならアルゴリズムを可視化してみたくなりますね!
JavaScript + d3.js でやってみました.
JavaScript の 64bit integer の扱いがあやしいので乱数計算部分をちょっといじっています. そのためか分布には偏りがある感じがしますが, アルゴリズムの概要をつかむには十分でしょう.
点それぞれがアイテムになり, アイテムにはランダムに ID が振られています. ID から JCH でバケット番号を計算し, 対応するバケットに追加しています. 横がバケットになっています.
ボタンを押すと, バケットがひとつ追加され, 各アイテムのハッシュを再計算します. 再度 JCH を適用してバケット番号を計算し, 変化のあったもの(増えたバケットの番号に対応するもの)をアニメーションさせています. 移動するアイテムが最小限になっているのが見て取れるかと思います.
欠点
- バケット番号は, 連番で 0 から n-1 で付けられている必要がある. 従って, 分散ストレージのようなアプリでは有益だが, Web 分散キャッシュのようなケースでは有益でない.
おまけ
2011 年の時点で Guava ライブラリに使われていた.
まとめ
- Jump Consistent Hash すごい
- 確率を制するものは世界を制する.
- 特許は申請していない(し, 申請の予定も今のところ無い)ので, 皆さんにたくさん使ってほしいようです.