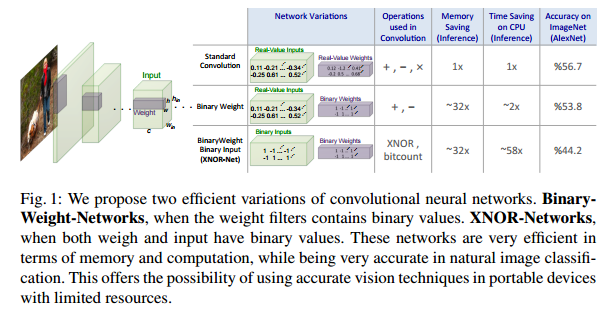
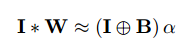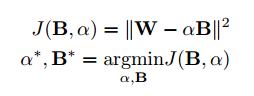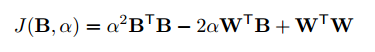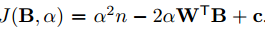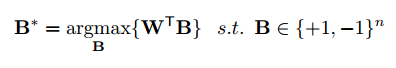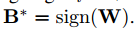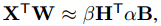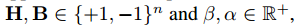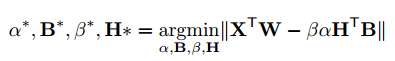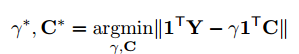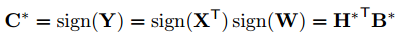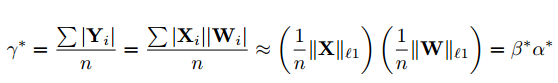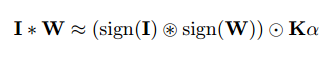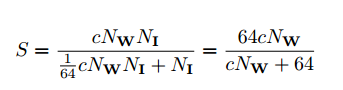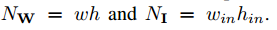XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks

この論文は、二値化(binarization)によってNeural Networkの高速化と省メモリ化を図るというものです。
binarizationの対象は、weightとinputです。
このbinarizationによりメモリ使用量が1/32、速度が58倍速くなっています。
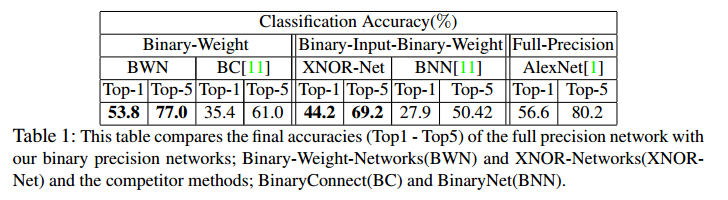
full 精度の性能と比較して2.9%以内の劣化にとどまっておりかつ、比較対象となっているBinaryConnectやBinaryNetと比べて16%性能が上回っています。

Deep Neural Networkでは、いろいろな分野で様々な成果をあげていますが、Parameter数が非常に多く、メモリと計算コストを大量に必要とします。例えば、この論文では性能比較にAlexNetを使用していて、AlexNetのParameter数は61Mで総容量は249MBになります。
Mobile機器などの計算資源が少ないDeviceに適応する場合に、こういったことは問題となってきます。

Binarizationのメリットとしては、
1. メモリ量がSingle Precisionと比較して1/32になる
2. Convolution演算がXNORとbitcountingになり高速化できる
という２つの点が挙げられます。

この論文では、Binary-Weight-Networksという重みのみ２値化したものと、XNOR-Networksという重みと入力の両方を２値化した２つのNetworkを提案しています。

Related Work

Approach	Description
Shallow networks	Shallow Networkでどんなdecision boundaryも描けることがわかっているが学習が困難でかつ、結局Parameter数がDeep Networkと同じぐらい必要で、それほどメリットがないので、この論文では一般的なDeep Neural Network構造を使用。
Compressing pre-trained deep networks	Pruning（枝狩り）で冗長性をなくすという方法がいろいろ行われている。weight decayもその一つ。weight decayはL2 regularization項を入れることで重みを小さくするというもの。その他にHashを使って同じHush KeyのWeightは同一Parameterにするというものもある。
Designing compact layers	Fully connected layerはParameter数が多いのでやめて、global average poolingにする方法や、ResNetのようにBottleneck構造にしてParameter数を減らすというものもある。
Quantizing parameters	Parameterの精度を制限する方法。+1/0/-1の３値という方法もある。ただし、その手法はBack Propagationの時のみ３値で、Test Phase、Forward Propagationはfull precisionで処理している。
Network binarization	この論文が属するApproach.この論文以外にもBinaryConnectやBinaryNetという手法がある。

Binary Convolutional Neural Network

変数の定義

変数	定義
$I={\cal I}_{l(l=1,...,L)}, I\in {\mathbb R}^{c\times win \times hin} $	$l^{th}$ layerの入力Tensor $(c, w_{in}, h_{in})$=channel数、画像のwidth, height
$W={\cal W}_{lk(k=1,...K^l)}, W\in {\mathbb R}^{c\times w \times h}$	$l^{th}$ layerの$k^{th}$ weight $(c, w, h)$=channel数、filterのwidth, height
$K^l$	$l$ layerのfilter数
$*$	convolutional operation
$\oplus$	掛け算なしのconvolutional operation
$B \in \{+1, -1\}^{c \times w \times h}$	binary filter
$\alpha \in {\mathbb R}^{+}$	scale factor (positive real value)

Binary Weight Network

Convoluation演算にbinarizationを適応します。基本は下記のようにbinary filter $B$とscaling factor $\alpha$に分解して近似するだけ。

なるべくもとの値に近い$B$と$\alpha$を求めたいので下記のように近似誤差を定義します。

展開すると下記のようになります。

ここで$B^TB$と$W^TW$は定数なので下記のように書けます。

$J(B, \alpha)$を最小化すればよいので、$\alpha$は正の値だから、$W^TB$を最大化するように$B$を求めると良い。

これを最大化するには$W$の要素$W_i$が$W_i \ge 0$のとき、$B_i=+1$に、$W_i \lt 0$のとき、$B_i = -1$にするとよい。

ということは。最適値$B^*$は下記のようになり、結局は$W$の符号を値とする行列になります。

$\alpha$の最適値は、$J(B,\alpha)$を$\alpha$に関して偏微分して$0$とおいて解くと下記のようになります。

\begin{eqnarray}
\frac{\partial J(B,\alpha)}{\partial \alpha}=2\alpha n - 2 W^TB^* = 0\\
\alpha^* = \frac{W^TB^*}{n}\\
\end{eqnarray}

これに$B^*$を代入すると$W$のL1ノルムを$n$で割ったものになります。

Training Binary-Weights-Networks

Training algorithmは下記の通り

要約すると、

weightを２値化 $B,A$を求める
Forward propagation　$(B\oplus I)\alpha$を使用
Back propagation $W$は２値化したもの${\cal {\tilde W}}$を使う
parameter $W$とlearning rateを更新する（update更新時だけbinary値を使わない）

update時にbinarizationしない理由は、update時の更新量は非常に小さいの更新後に２値化するとこれらの変化が消え去り、Parameterが更新されなくなるため。

一旦Trainingが終われば、実数値のweightは必要なく、推定時はbinary weightだけでforward propagationを行います。

XNOR-Networks

weightとinputの両方を2値化する。これによりconvolution演算がXNORとbitcounting演算だけになります。

先ほどと同様にbinaryの行列とscalerに分離します。

同じように下記を満たす $\alpha*$, $\beta*$, $B^$, $H^$を求めます。

ここで$Y_i = X_iW_i$のように要素ごとの積を計算したものを$Y_i \in {\mathbb R}^n$とする。
さらに$C_i = H_iB_i$と$\gamma = \beta\alpha$とおくと、上記の式は下記のように書けます。

これは掛け算だけ先に計算して、$1^T$と内積を取ることで、後で足し算を行っていることに相当します。$1^T$は要素がすべて１のベクトル。
これで最初の時と同じように$C$と$\gamma$の最適値が求められ下記のようになります。

Binary Convolution

異なる場所のbinary convolutionを計算するときに重複して計算している部分があります。
それを示したのが下図の中段(2)の赤い時の部分。
重なっている部分を計算するのは無駄なので、(3)のようにchannel方向に絶対値の平均を計算して$A$を求めて、その後で2D filter $k \in {\cal R}^{w \times h}$とconvolution演算をする。ただし、$k$の要素は$k_{ij}=\frac{1}{w \times h}$。

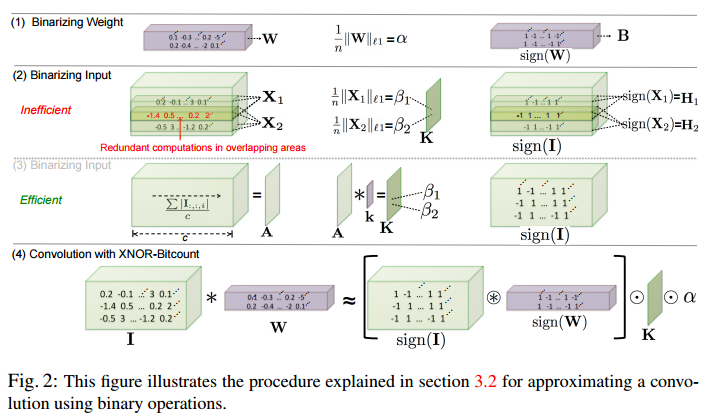
最終的にinputとweightのconvolutionは下記のように分解される。

$\circledast$はXNORとbitcountによるconvolutional operation。
$\odot$は要素ごとの掛け算。

Training XNOR-Networks

一般的なCNNは、
1. Convolutional
2. Batch Normalization
3. Activate
4. Pooling
の順で構成される。
２値化されたデータにmax poolingを適応しても、+1にしかならないので、lossが大きいから順番を右のように変更する。

Batch Normalization
BinActiv
BinConv
Pooling

BinActivでは${\rm K}$と${\rm sign(I)}$を計算する。
sign function$q=sign(r)$のgradientは、BinaryNetと同じように$g_r=g_q1_{|r|\le1}$とする。

BinConvではを計算する。

Experiments

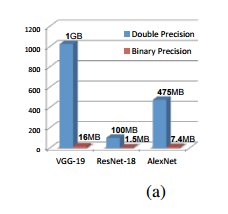
memory効率の比較

各モデル毎のdouble precisionとbinary precisionの必要メモリ量の比較

operation数の比較

standard convolutionとbinary convolutionのoperation回数の比率は下記のようになる。
64は一般的なCPUには64bit operationがあるというところから来ている値。

左が$c$を変えた時のグラフで、右が$N_w$を変えた時のグラフ

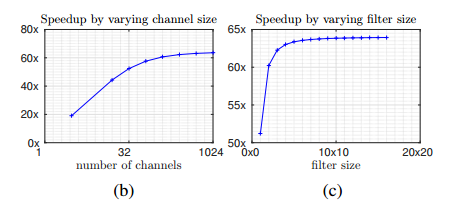
ResNetのArchitectureから$c=256, n_I=14^2, n_W=3^2$とした時、$S=62.27$になる。ただしoverheadがあるので、実際には１ convoluation演算あたり58倍高速化される。
ただし、グラフ(b)をみると$c$が小さい値ではそれほど高速化されない。例えばfirst layerやlast layerでは一般的にchannel数が少ないのでBinaryNetと同じようにbinarizationは行わない。

Image Classification on ILSVRC2012

Dataset

・ILSVRC2012
・1.2M Training Data
・1K categories
・50K validation image

Networks

・AlexNet
・5 convolutional layer and 2 fully connected layer
・Parameter数 61M

比較対象

BinaryConnect
・forward propagation, backward propagation時binarizationを行う
・update時はreal valueを使用する
・deterministic binarizationとstochastic binarizationが記載されているが、deterministicを使用。
　deterministicではweightが0以上の時は+1,それ以外は-1とする。
BinaryNet
・推定時と学習時のgradient計算時にweightとactivationをbinarizationする

Training

・画像の縦横の短い方が256になるようにresizeする
・224x224でrandom croppingする
・epoch数16
・batch size 512
・SGD (momentum 0.9) Binary-weight-networksとBinaryConnect比較時
・ADAM XNOR-NetworksとBInaryNet比較時
・learning rate 初期値 0.1 4 epoch毎に0.01 減衰させる

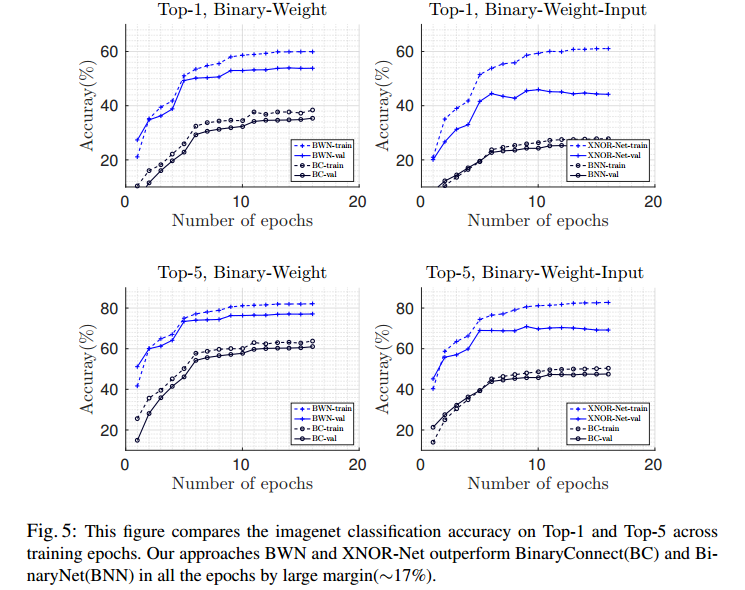
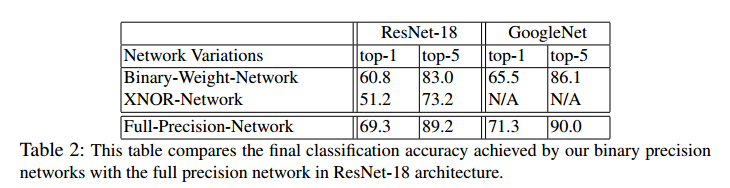
結果は下記の通りで、Binary-Weight-Networks,XNOR-Networksともに比較対象と比べて17%ぐらい性能が良い。
dashedがtraining dataでsolidがvalidation dataの結果

Residual Net/GoogleNet Variantで比較

・比較対象はFull Precision、Binary-Weight-Networks,XNOR-Networks
ResNet
・ResNetは18 layerを使用
・short cut connectionとしてA, B, CがあるがBを使用
　A,B,Cはshortcutした時の合流時点で次元数が異なる場合の処理の違い
　　A Zero Padding
　　B 次元数が異なるところだけProjectionで同じ次元にする
　　C 次元数の違いによらず全部Projectionする
・画像の縦横の短い方を256か480にRandomでResizeする
・224x224でrandom croppingする
・epoch数 58
・batch size 256
・learning rate 初期値 0.1 30epochと40epochで0.01 減衰させる
・Test時は中心部分を224x224でcropして使用する

GoogleNet Variant
・straightforward network (no branching)
・21 convolutional layer
・filter size 1x1, 3x3
・画像の縦横の短い方を256か320にRandomでResizeする
・224x224でrandom croppingする
・epoch数 80
・batch size 128
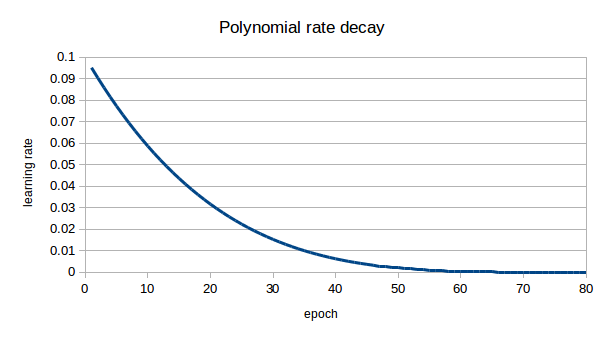
・learning rate 初期値 0.1 polynomial rate decay $\beta=4$
・Test時は中心部分を224x224でcropして使用する
polynomial rate decayの記載は無いが多分こんな感じ

learning rate=0.1\times (1-\frac{epoch}{80})^4

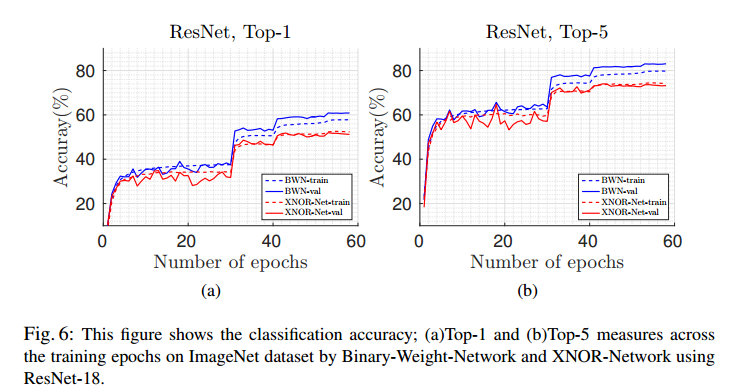
結果は下記の通り
dashedがtraining dataでsolidがvalidation dataの結果
Binary-Weight-Networksの方が性能が良い。
Full Precisionと比べて性能はそれほど劣化していないが、他手法との比較が無いのでよくわからない。

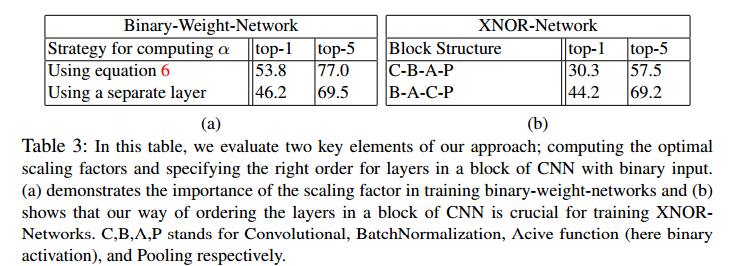
Scaling factorとblock structureの比較

左：scaling factorを固定パラメータとした時の比較
scaling factorの有効性チェックのため

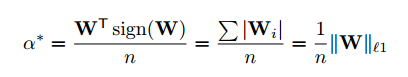
右：block structure比較
一般的なStructureと提案手法のStructureを比較して有効性をチェックするため
C-B-A-Pが一般的なStructureでB-A-C-Pが提案手法のStructure

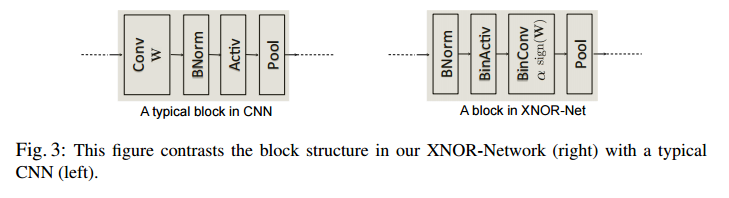
どちらも性能が向上している。

最後に

結局のところ、weightとinputを符号ビットとscale factor(filter領域の絶対値平均)に分解して効率化したという感じでしょうか。
構造はなるべく近似誤差が大きくならないように順番をアレンジしています。

[Survey]XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks