[DL]Back Propagationって何？

Back propagation

back propagationは勾配を求める手法です。
勾配は、Parameterの最適値を求めるのに使用します。Deep Learningでは一般的に、Parameterを求めるためにGradient Descentという手法が使われます。
Gradient Descentは学習データと推定値の差をCost Functionとして、そのCost Functionが最小となるParameterを求める時に使われます。
　Cost Functionが$C(w)=w^2+aw+b$のような形であれば解析的に求めることは可能ですが、通常はこのような形ではないため解析的に求められません。
Cost Functionがどのような形をしているかもわからない場合にどうやって最小値となるParameterを求めらたいいでしょうか？
一つの戦略として、とりあえず$w$をランダムに変えて最小値を探すという方法も考えられますが見るからに効率が悪そうです。
　何かヒントとなる情報を元にCost Functionが最小となるParameterを探せると効率が良さそうです。
そのヒントとなる情報が勾配になります。Gradient Descentは、「目隠しをしながらCost Functionという谷の谷底をコンパスを片手に探す」という感じです。そのコンパスの役目をするのが勾配になります。
　例えば勾配が正ならば、Parameterを大きくするとCostが増加するということを教えてくれます。
なので勾配が正の時はパラメータを減らす方向に更新することになります。
式で書くと以下のようになります。ここで$\frac{\partial C(w)}{\partial w}$が$w$に関する勾配になります。

w \leftarrow w - \lambda \frac{\partial C(w)}{\partial w}

Deep LearningではStochastic Gradient Descentと言われる手法が使われますが、これは単純に言うと全学習データで$\frac{\partial C(w)}{\partial w}$を計算するのは時間もかかって大変なので、少ないデータで$\frac{\partial C(w)}{\partial w}$を求めてそれを推定値として使うというものです。

back propagationに関して、式で丁寧に説明してくれているものは世の中に沢山あるので、今回は実際の流れを説明したいと思います。
back propagationには微分のchain ruleというものを使用します。

例えば$y = (ax+b)^2$の微分を求める時に$t=ax+b$とおいて下記のようにして求めます。これがいわゆる微分のchain ruleです。

\begin{equation*}
y = (ax+b)^2\\
t = ax+b\\
y = t^2\\
\frac{\partial y}{\partial x} = \frac{\partial y}{\partial t}\frac{\partial t}{\partial x}=(2t)(a)=2a(ax+b)\\
\end{equation*}

実際に計算してみる

以下のようなCost Function $C(w)$の勾配を求めてみます。
$x$は入力、$w$,$b$はParameter、$y$は推定値、$y^{'}$は正解データです。

\begin{equation*}
y=wx+b\\
C(w) = (y^{'}-y)^2\\
\end{equation*}

ここでParameterと推定値以外のデータを下記のようにします。Parameterは求めたい値ですし、推定値はParameterと入力が決まれば求まります。

$x=2, w=3, b=1, y^{'}=5$

解析的に解く

とりあえず後で正しく求められているか確認するために頑張って勾配を求めてみます。

\begin{eqnarray*}
C(w) & = & (y^{'}-wx-b)^2\\
\frac{\partial C(w)}{\partial w}&=&-2(y^{'}-wx-b)x=8\\
\frac{\partial C(w)}{\partial b}&=&-2(y^{'}-wx-b)=4\\
\end{eqnarray*}

$w$と$b$に関する勾配は、それぞれ$\frac{\partial C(w)}{\partial w}=8,\frac{\partial C(w)}{\partial b}=4$になります。

back propagationで解く

次にback propagationで勾配を求めてみます。
ここでComputational Graphというものを導入します。Computational Graphはただ計算式をグラフ化したものです。丸の中が演算で左から右の方向データが流れます。途中経過の値にも変数を割り当てます。

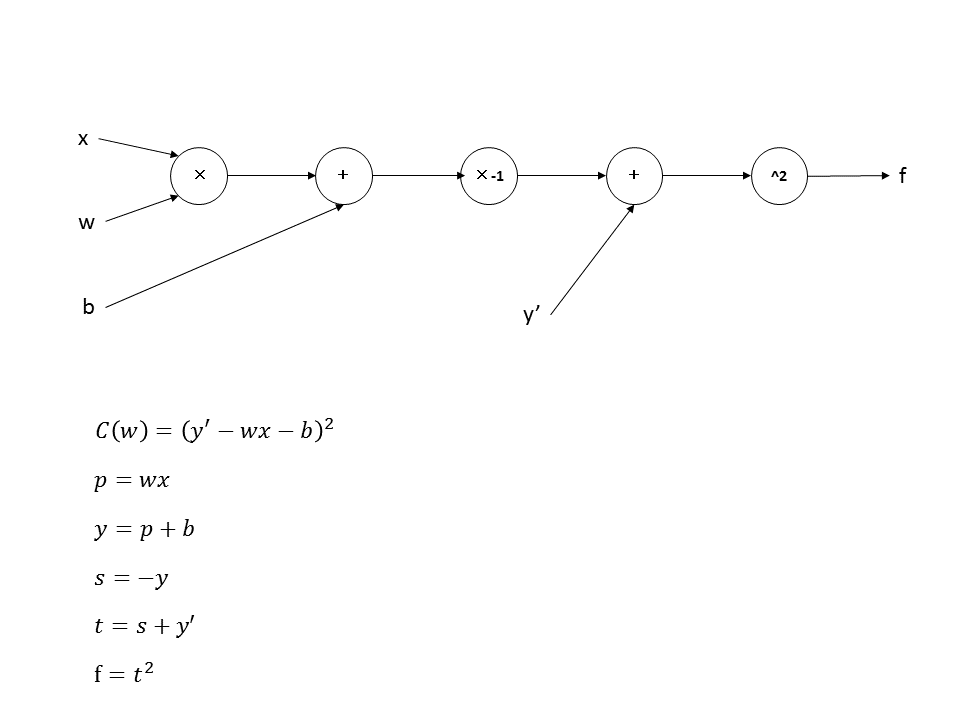
まずforward propagationを計算して値を線の上に書いていきます。

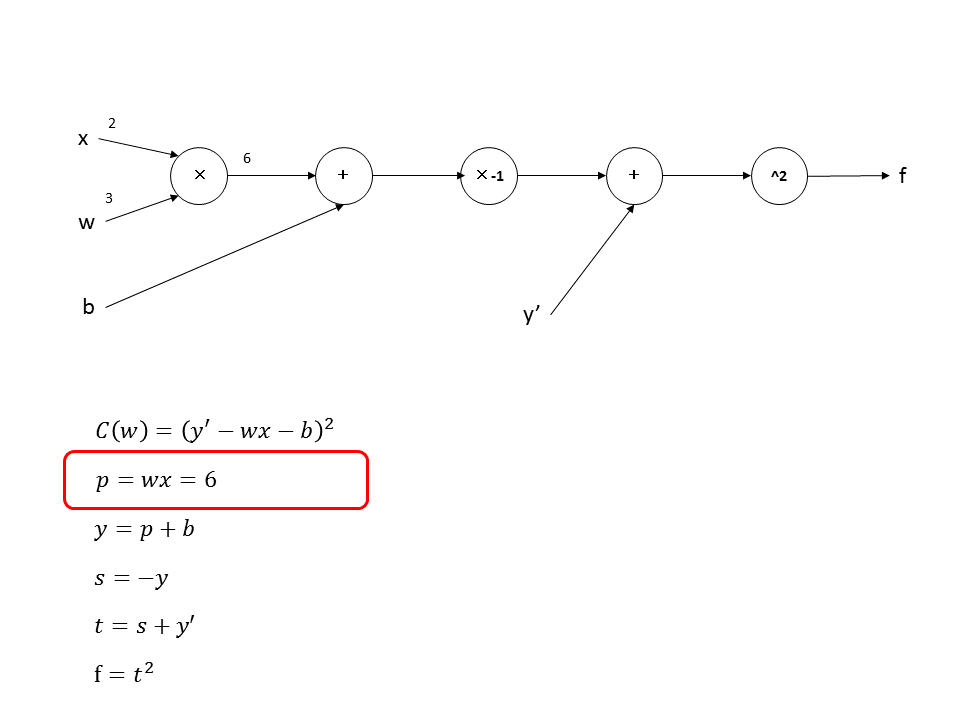
forward propagationを最後まで計算すると下記のようになります。

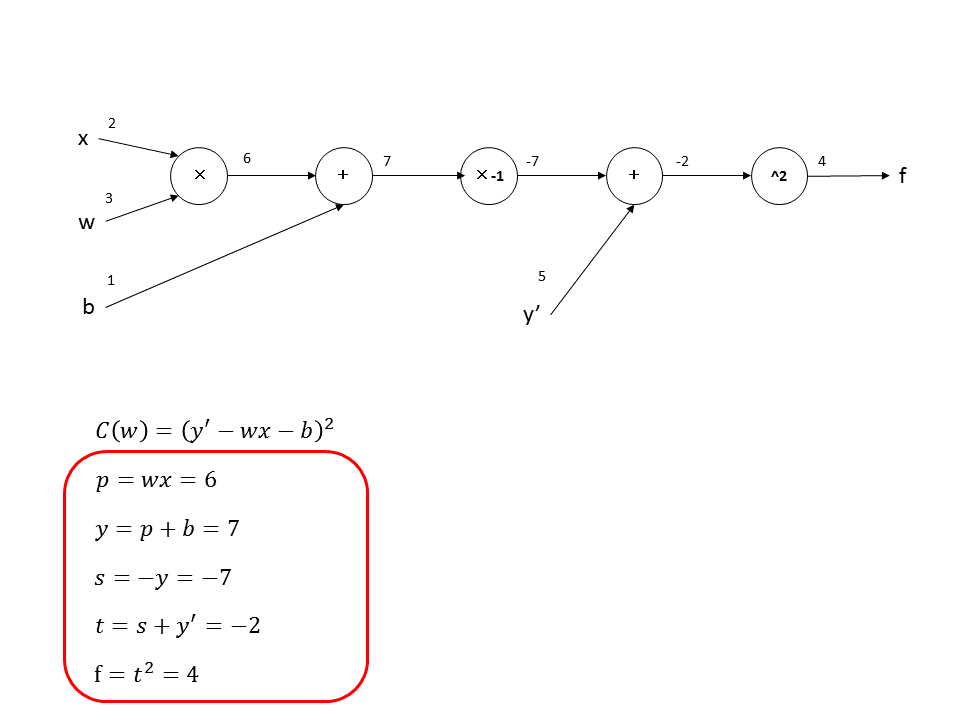
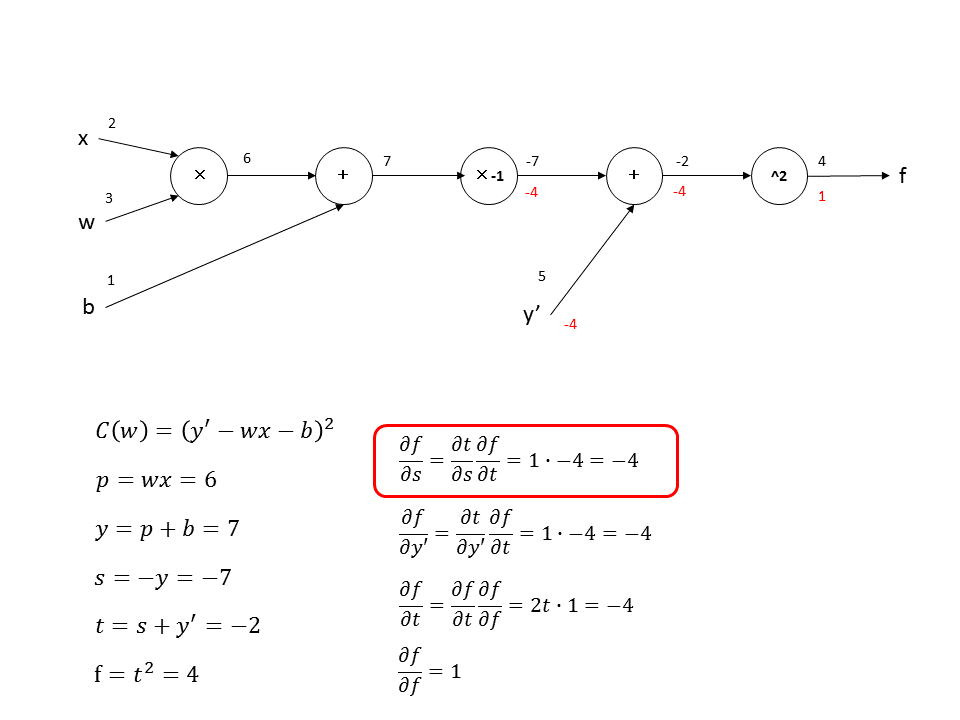
次にback propagationを計算していきます。$f$を$f$に関して偏微分します。$\frac{\partial f}{\partial f}=1$なので、赤字で下記のように書きこみます。

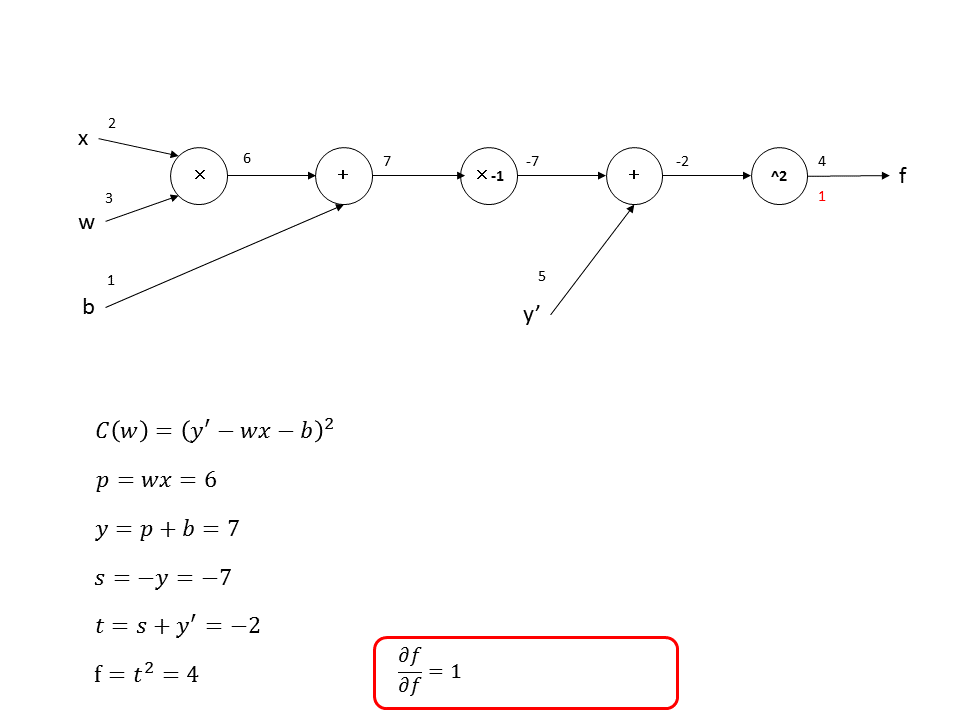
次に、$f$を$t$に関して偏微分します。ここでchain ruleを使って計算すると、$\frac{\partial f}{\partial t}=\frac{\partial f}{\partial t}\frac{\partial f}{\partial f}=2t\cdot 1=-4$となります。

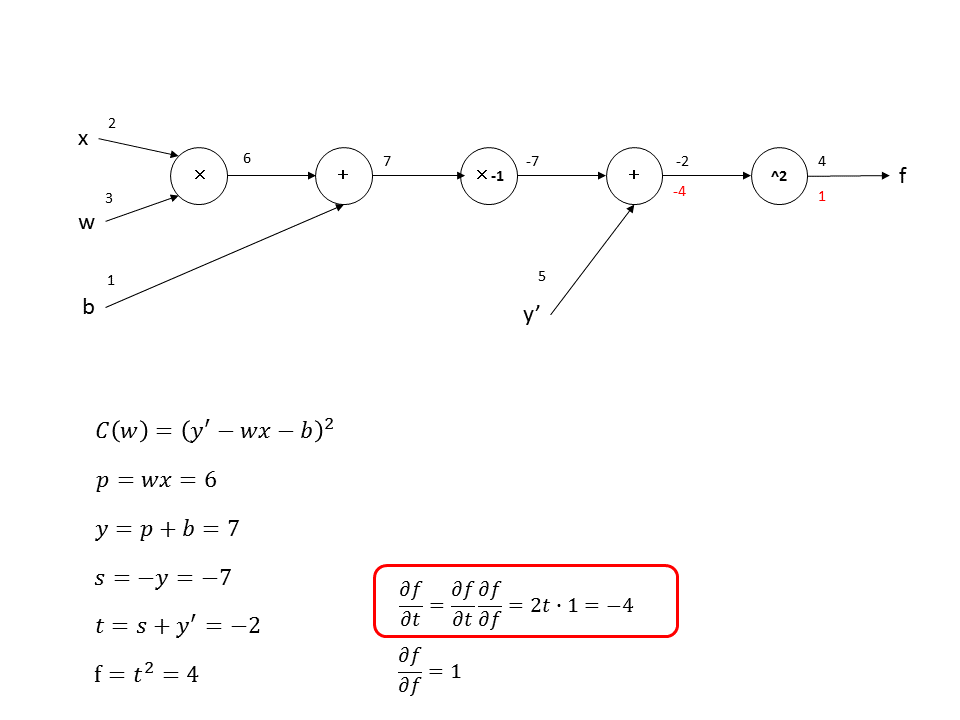
次に、$f$を$ｙ^{'}$に関して偏微分します。chain ruleを使用して計算するときに、前で計算した偏微分$\frac{\partial f}{\partial t}$が必要になり、$\frac{\partial f}{\partial y^{'}}=\frac{\partial t}{\partial y^{'}}\frac{\partial f}{\partial t}=1\cdot -4=-4$となります。

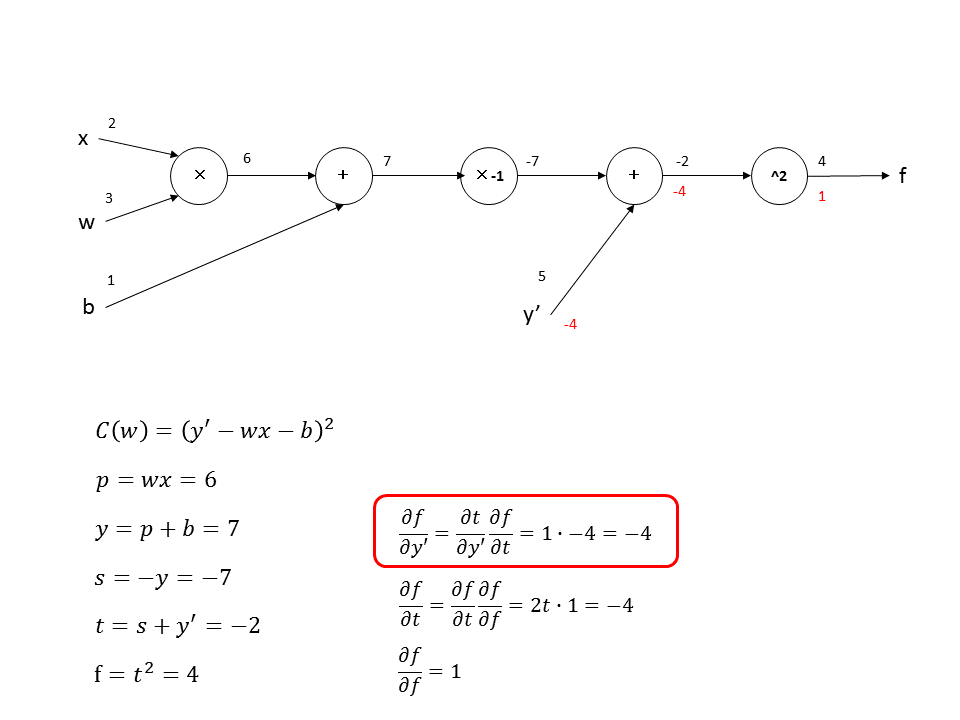
次に、$f$を$s$に関して偏微分します。ここでも前で計算した偏微分$\frac{\partial f}{\partial t}$が必要になり、$\frac{\partial f}{\partial s}=\frac{\partial t}{\partial s}\frac{\partial f}{\partial t}=1\cdot -4=-4$となります。
足し算の時はchain ruleの片方の偏微分が$1$になるので、前に計算した偏微分の値が両方へ伝搬する形になります。

$-1$倍は前の偏微分の値の符号が反転して、足し算はその値が伝搬するので下記のようになります。

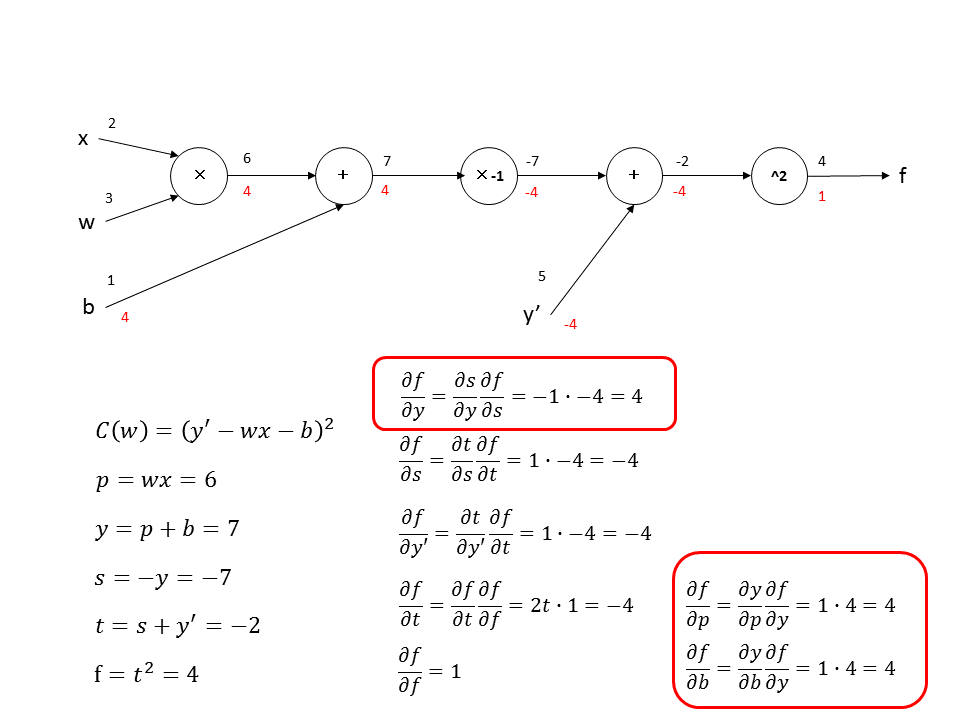
次に$f$を$w$と$x$に関して偏微分した値を計算します。$\frac{\partial f}{\partial w}=\frac{\partial p}{\partial w}\frac{\partial f}{\partial p}=x\cdot 4=8$と$\frac{\partial f}{\partial x}=\frac{\partial p}{\partial x}\frac{\partial f}{\partial p}=w\cdot 4=12$となります。

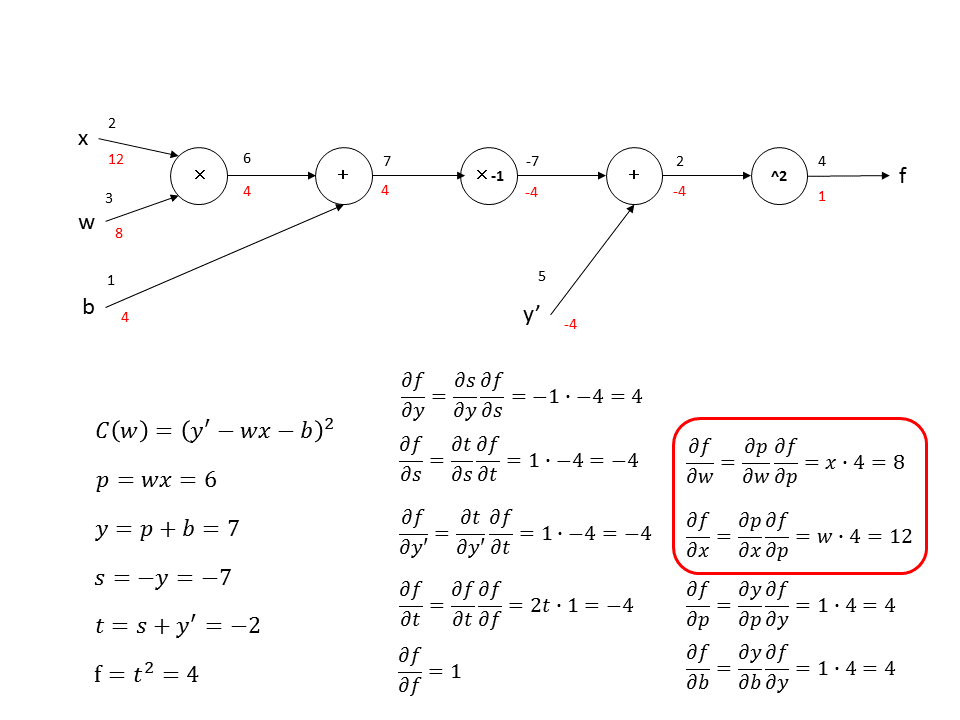
$\frac{\partial f}{\partial w}$と$\frac{\partial f}{\partial b}$の計算結果を解析的に求めた値と比較すると同じになっていることがわかります。

tensorflowにて値を確認してみた

back propagationの動作を確認するために、tensorflowでコードを書いて試してみました。

上記式と記号はそのままですが$y^{'}$だけy_にしました。
出力の最初の３行でforward propagationの結果が確認できます。
次の３行で各変数に関する勾配の結果が確認できます。
GradientDescentOptimizerの実行後、再度変数を確認すると各変数が更新されているのがわかります。
learning rateは1.0にしたので、単純に勾配が引かれた値になっています。
入力$x$,$y\_$も更新されているので、このままもう一度optimizerを実行すると大変なことになるので、実際はplaceholderにした方がいいです。これでoptimizerが何を計算しているかわかったかと思います。

python

import tensorflow as tf
import numpy as np

w = tf.Variable(tf.constant([3.]))
x = tf.Variable(tf.constant([2.]))
b = tf.Variable(tf.constant([1.]))
y_ = tf.Variable(tf.constant([5.]))

p = w*x
y = p+b
s = -y
t = s +y_
f = t*t

gx, gb, gw, gp, gy, gy_,gs, gt, gf = tf.gradients(f, [x, b, w, p, y, y_,s, t, f])

init = tf.initialize_all_variables()

opt = tf.train.GradientDescentOptimizer(1.0)
train = opt.minimize(f)

with tf.Session() as sess:
    sess.run(init)
    print 'x:%.2f, w:%.2f, b:%.2f' % (sess.run(x), sess.run(w), sess.run(b))
    print 'p:%.2f, y:%.2f, y_:%.2f'% (sess.run(p), sess.run(y), sess.run(y_))
    print 's:%.2f, t:%.2f, f:%.2f' % (sess.run(s), sess.run(t), sess.run(f))

    print '---------- gradient ----------'
    print 'gx:%.2f, gw:%.2f, gb: %.2f' % (sess.run(gx), sess.run(gw), sess.run(gb))
    print 'gp:%.2f, gy:%.2f, gy_:%.2f' %(sess.run(gp), sess.run(gy), sess.run(gy_))
    print 'gs:%.2f, gt:%.2f, gf:%.2f' %(sess.run(gs), sess.run(gt), sess.run(gf))
    print '---------- run GradientDescentOptimizer ----------'
    sess.run(train)

    print 'x:%.2f, w:%.2f, b:%.2f' % (sess.run(x), sess.run(w), sess.run(b))
    print 'p:%.2f, y:%.2f, y_:%.2f'% (sess.run(p), sess.run(y), sess.run(y_))
    print 's:%.2f, t:%.2f, f:%.2f'%(sess.run(s), sess.run(t), sess.run(f))

    print '---------- gradient ----------'
    print 'gx:%.2f, gw:%.2f, gb: %.2f' % (sess.run(gx), sess.run(gw), sess.run(gb))
    print 'gp:%.2f, gy:%.2f, gy_:%.2f' %(sess.run(gp), sess.run(gy), sess.run(gy_))
    print 'gs:%.2f, gt:%.2f, gf:%.2f' %(sess.run(gs), sess.run(gt), sess.run(gf))

実行結果

x:2.00, w:3.00, b:1.00
p:6.00, y:7.00, y_:5.00
s:-7.00, t:-2.00, f:4.00
---------- gradient ----------
gx:12.00, gw:8.00, gb: 4.00
gp:4.00, gy:4.00, gy_:-4.00
gs:-4.00, gt:-4.00, gf:1.00
---------- run GradientDescentOptimizer ----------
x:-10.00, w:-5.00, b:-3.00
p:50.00, y:47.00, y_:9.00
s:-47.00, t:-38.00, f:1444.00
---------- gradient ----------
gx:-380.00, gw:-760.00, gb: 76.00
gp:76.00, gy:76.00, gy_:-76.00
gs:-76.00, gt:-76.00, gf:1.00