最適化の目的関数
サポートベクターマシンのコスト関数は以下のように定義される。
J(\theta)=C\sum_{i=1}^{m}y^{(i)} cost_1 (\theta^T x^{(i)} )+(1-y^{(i)} )cost_0 (\theta^T x^{(i)} )+\frac{1}{2}\sum_{j-1}^{n}\Theta_{j}^{2}
このコスト関数を最小化する$\theta$を用いて、仮説関数$h_\theta (x)$が正負を判断する。
ロジスティック回帰のコスト関数は以下の通りなので、違う点はいくつかある。
J(\theta)=\frac{1}{m}\sum_{i=1}^{m}y^{(i)}(- \log (h_{\theta}x^{(i)} ))+(1-y^{(i)} )(- \log (1-h_{\theta}(x^{(i)})))+\frac{\lambda}{2m}\sum_{j-1}^{n}\Theta_{j}^{2}
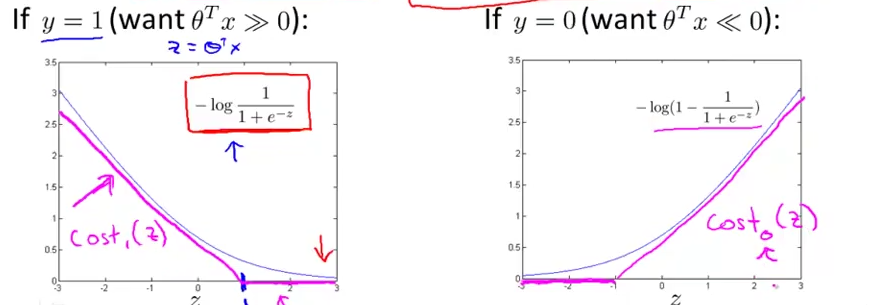
・$cost_1 (\theta^T x^{(i)} )$, $cost_0 (\theta^T x^{(i)} )$と$- \log (h_{\theta}x^{(i)} )$, $- \log (1-h_{\theta}(x^{(i)}))$の差
下記のマゼンタ色の線のようにサポートベクターマシンではロジスティック回帰に近いが、曲線ではなく直線の組み合わせで成り立っている。
・$\frac{1}{m}$がない
SVMのコスト関数において$\frac{1}{m}$が最小化の解に影響がないため除去されている
・$C$と$\lambda$の差
ロジスティック回帰では正規化パラメータ$\lambda$を小さくするとオーバーフィッティングしていたが、SVMではCを大きくするとオーバーフィッティングする。
極端に言えば$J(\theta)=Ca+b$が$J(\theta)=a+\lambda b$となったようなもので、前半部分か後半部分どちらを調整することで重みをコントロールするかという違い。なので実質的には$C=\frac{1}{\lambda}$といえる。
・仮説関数の出力
ロジスティック回帰では仮説関数によって答えが正である確率が出力されたが、SVMでは$\Theta^T x\geq 0$なら$h_\theta (x)=1$でそれ以外なら$h_\theta (x)=0$と正負の判断が行われる
ラージマージン分類器
SVMは大きなマージンの分類器と呼ばれる。以下の様なサンプルが与えられた際に、データから大きな距離をとった黒い線で決定境界を設定する。これの決定境界とそこから最も近いデータの間をマージンと呼び、SVMではこのマージンを最大にしようと上記の最適化によって決定境界を設定する。

また下記のようなデータが与えられた時は、Cの値が大きいほど外れ値の影響を強く受け、マゼンタ色のような識別境界を引くことになる。

カーネル
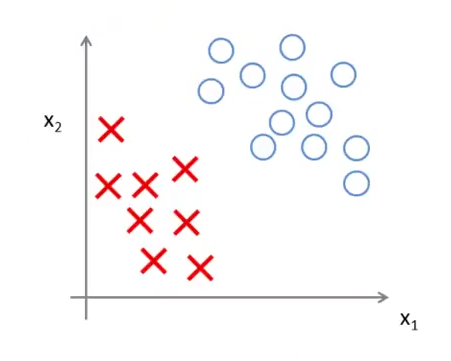
下記のような線形分類できない分類問題をSVMで解く場合、SVMではカーネルという概念を用いる。
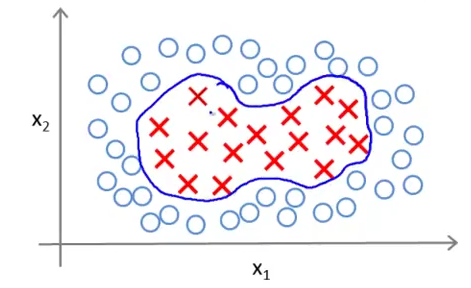
ここでは入力値$x^{(i)}$を利用して新たな特徴$f$を定義し、それを用いて仮説を構築する。その手続について以下で述べていく。
例えば上の図同様、$x^{(i)}$が二次元ベクトルの値だとした場合は、
まずその二次元空間内にランドマークとして幾つかのポイントを設定する。例えば下図のように3つのランドマーク$l^{(1)}$、$l^{(2)}$、$l^{(3)}$を設定したとする。
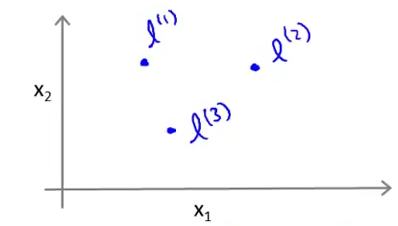
入力$x$とこれらのランドマークの近似値を新たに$f$と定義し、この$f$をあらたな特徴量に用いて仮説関数を設計する。この近似値を求める関数を数学的にはカーネルといい、この場合は特にガウシアンカーネルと呼ばれる。
f_i=similarity(x, l^{(i)}) = exp(-\frac{||x-l^{(i)}||}{2\sigma})
この式は、$x\approx l^{(i)}$なら $f_i\approx 1$
$x$が$l^{(i)}$から離れているなら$f_i\approx 0$となる。
$\sigma$はガウシアンカーネルのパラメーターで、
これを大きくなると、$l^{(i)}$から離れるに連れて$f_i$はゆるやかに1から0に近づき、
これが小さくなると、$l^{(i)}$から離れるに連れて$f_i$は急に1から0に近づく。
このように各ランドマークごとに新たな特徴$f_i$を求め、それらを用いて仮説関数を設計する。
上記の図のようにランドマークを3つ設定した際は、
\theta_0 + \theta_1f_1 + \theta_2f_2 + \theta_3f_3
というような仮説関数となり、これが0以上なら1で、以下なら0となる。
ランドマークの設定方法
ランドマークの設定方法の1つとしてはトレーニングデータをそのままランドマークに設定することである。つまり、m個のトレーニングデータに対してランドマークを設定し、$l^{(i)}$と各トレーニングデータとの近似値$f_1^{(i)}…f_m^{(i)}$を積み上げて新たな特徴ベクトル$f^{(i))}$を設定する。
$\theta$がすでに与えられている際はこの特徴量を用いて$\theta^T f\geq0$であればy=1と予測することができる。
また$\theta$が与えられていない場合、特徴$f$を用いて下記の数式を解くことでもとめることができる。
min C\sum_{i=1}^{m}y^{(i)} cost_1 (\theta^T f^{(i)} )+(1-y^{(i)} )cost_0 (\theta^T f^{(i)} )+\frac{1}{2}\sum_{j-1}^{n}\Theta_{j}^{2}
SVMを使う
実際に使うとき
わざわざ数式を実装しなくてもlibsvmとかliblinearとかを使えばいいよ
必要なのは$C$を決めることとカーネルを選ぶこと
線形カーネル
特徴量nが多くてトレーニングデータmが少ない時は、十分なデータがないとオーバーフィッティングしやすいので、線形カーネルを使用する(カーネルを使用しない)
ガウシアンカーネル
- 特徴量nが少なく、トレーニングデータmが多い時にはガウシアンカーネルを使用する。
- この場合はパラメータ$\sigma$を決定する必要があり、この値はバイアスとバリアンスのトレードオフで、大きければ高バイアス低バリアンスになるし、小さければその逆になる。
- ガウシアンカーネルを使う場合、パッケージによってはカーネル関数を実装しなくてはならない時もある。
- ガウシアンカーネルを使う場合特徴量のスケールが違いすぎる場合はフィーチャースケーリングしましょう
その他のカーネル
- 多項式カーネル
- 文字列カーネル
- カイ2乗カーネル
- ヒストグラム交差カーネル
などなど
複数クラスの分類
ロジスティック回帰でやったものと同様にone-vs-all方式で解く
SVMはどういう時に使うのか
- 特徴量nがトレーニングデータ数mと比較して多い時(ex. n=10,000, m=10...10,000)はロジスティック回帰か線形カーネルSVM
- nが少なくてmが中くらい場合(ex. n=1...1,000, m=10...50,000)はガウシアンカーネルSVM
- nが少なくてmが多い場合(ex. n=1...1,000, m=50,000+)は手動で特徴量を増やしてロジスティック回帰か線形カーネルSVMを使う
ロジスティック回帰と線形SVMは似たような挙動をする。SVMの本領は複雑な非線形のデータを学習するガウシアンカーネルにあり、ガウシアンカーネルが使える条件が整っていることはよくある。
またこれらすべての場合にニューラルネットワークは使用できるが、場合によっては遅いので、そういった時にSVMをつかうとよろし。