Pythonで数値シミュレーションの2回目です.
今回は拡散律速凝集(DLA)についてのシミュレーションを紹介したいと思います.
この内容は計算物理学のよい教科書である,
 |
計算物理学入門 (2000/12) ハーベイ ゴールド、ジャン トボチニク 他 商品詳細を見る |
を参考にしています.
雪の結晶や地質学的な断層における稲妻形のひび割れの形成,バクテリアのコロニーの成長など,自然界には基本となる単位をランダムに付け加えていくことで成長するものを多く見ることができます.よく知られたモデルの1つに拡散律速凝集(Diffusion-Limited Aggregation: DLA)があります.このモデルは,ランダムな運動がいかに美しい自己相似なクラスターを生み出すかを示す例となっています.
クラスターの成長のステップは,
- 1つの種の粒子で1つの格子点を占有
- 種を中心とする円の周囲から1つの粒子を放出
- その粒子をランダムウォークさせ,
- 1つの周辺の点に到達するとそこに付着→2へ
大きなクラスターが形成されるまで,このプロセスを繰り返します(典型的には数千から数100万回の程度).また,計算量を少なくするため,3の段階でクラスターから遠くに行き過ぎた粒子は取り除き,2からやり直すことにします.
この操作を実際に実現するには,格子を表す行列と,占有された格子点の周辺の点を記録する配列が有ればよいことが分かります.ランダムウォークの部分は,何度も流用しているものですが,一様乱数を生成し,その値の大きさで上下左右の方向を決めるものです.また,実際にシミュレーションを行うと,クラスターから遠い位置でのランダムウォークが,CPU時間のほとんどとなり,効率が悪くなってしまうため,クラスターから遠いところではランダムウォークの歩幅が大きくなるようにしてみました.実際にシミュレーションを実行(N=200, 500, 1000の場合についてクラスターを生成)した様子をキャプチャしたので,以下で確認できます.
何も編集してないのでグダグダですがw
a,b,cというのは教科書の問題のa,b,cを意味しており,aはエントリーボックスで指定した個数の粒子でクラスターを作成するものです.b,cは,モンテカルロ・シミュレーションによって付着確率を求めるものと,フラクタル次元を実際に求めるものです.興味がある方は,ソースコードを参照してください.
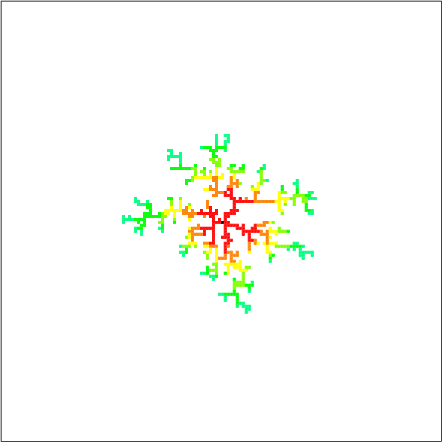
また,N=500のとき得られたクラスターは以下のようになりました.
リンク先(らくらく化学実験 - 美しい銀樹を作る)の銀樹の画像と比べても,よく似てると思いませんか?実際,ランダムウォークは拡散と等価なので,このシミュレーション自体は,まるっきり金属樹の生成を基にしていると言ってもよく,当然出来上がった図形の形はよく似ているのです.
以下にソースコードを全て載せておきます.
Canvasの保存のための関数prは,これからもよく使うことになりそうです.SetParameterも長く使っているクラスの一つです.もう少しまとめたい気持ちもありますが,現状これで困っていないので,しばらくはこのまま使い続けると思います.
# ! /usr/bin/env python
# -*- coding:utf-8 -*-
#
# written by ssh0, August 2014.
from Tkinter import *
import numpy as np
import matplotlib.pyplot as plt
import random
import time
class DLA(object):
def __init__(self, N, view=True, color=True):
self.r = 3
self.N = N
self.view = view
self.color = color
self.L = int(self.N**(0.78))
if self.view:
self.default_size = 640 # default size of canvas
self.rsize = int(self.default_size/(2*self.L))
if self.rsize == 0:
self.rsize = 1
fig_size = 2*self.rsize*self.L
self.margin = 10
self.sub = Toplevel()
self.canvas = Canvas(self.sub, width=fig_size+2*self.margin,
height=fig_size+2*self.margin)
self.c = self.canvas.create_rectangle
self.update = self.canvas.update
self.sub.title('DLA cluster')
self.c(self.margin, self.margin,
fig_size+self.margin, fig_size+self.margin,
outline='black', fill='white')
self.canvas.pack()
self.start_time = time.time()
def grow_cluster(self):
lattice = np.zeros([self.L*2+1, self.L*2+1], dtype=int)
# 種の格子点
self.center = self.L
lattice[self.center, self.center] = 1
if self.view:
c = self.c
rect = c((2*self.center-self.L)*self.rsize+self.margin,
(2*self.center-self.L)*self.rsize+self.margin,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
outline='black', fill='black')
rn = np.random.rand
def reset():
"""初期点の選択"""
theta = 2*np.pi*rn()
x = int((self.r+2)*np.cos(theta))+self.center
y = int((self.r+2)*np.sin(theta))+self.center
return x, y
x, y = reset()
l = 1
n = 0
while n < self.N:
# クラスターの周辺から遠いところでは歩幅を大きくする
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
if r > self.r+2:
l = int(r-self.r-2)
if l == 0: l = 1
else:
l = 1
# ランダムウォーク
p = rn()*4
if p < 1:
x += l
elif p < 2:
x -= l
elif p < 3:
y += l
else:
y -= l
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
# 中心点から離れた点で過程をやり直す
if r >= 2*self.r:
x, y = reset()
continue
judge = np.sum(lattice[x-1,y]+lattice[x+1,y]
+lattice[x,y-1]+lattice[x,y+1])
# 粒子をクラスターに取り込む
if judge > 0:
lattice[x, y] = 1
# 描画
if self.view:
if self.color:
colors = ['#ff0000', '#ff8000', '#ffff00', '#80ff00',
'#00ff00', '#00ff80', '#00ffff', '#0080ff',
'#0000ff', '#8000ff', '#ff00ff', '#ff0080']
color = colors[int(n/100)%len(colors)]
else:
color = "black"
rect = c((2*x-self.L)*self.rsize+self.margin,
(2*y-self.L)*self.rsize+self.margin,
(2*(x+1)-self.L)*self.rsize+self.margin-1,
(2*(y+1)-self.L)*self.rsize+self.margin-1,
outline=color, fill=color)
self.update()
# rmaxの更新
if int(r)+1 > self.r:
self.r = int(r) + 1
x, y = reset()
n += 1
else:
if self.view:
self.end_time = time.time()
t = self.end_time-self.start_time
print "done; N = %d, time = " % self.N + str(t) + ' (s)'
return lattice
class SetParameter():
def show_setting_window(self, parameters, commands):
""" Show a parameter setting window.
parameters: A list of dictionaries {'parameter name': default_value}
commands: A list of dictionary {'name of button': command}
"""
self.root = Tk()
self.root.title('Parameter')
frame1 = Frame(self.root, padx=5, pady=5)
frame1.pack(side='top')
self.entry = []
for i, parameter in enumerate(parameters):
label = Label(frame1, text=parameter.items()[0][0] + ' = ')
label.grid(row=i, column=0, sticky=E)
self.entry.append(Entry(frame1, width=10))
self.entry[i].grid(row=i, column=1)
self.entry[i].delete(0, END)
self.entry[i].insert(0, parameter.items()[0][1])
self.entry[0].focus_set()
frame2 = Frame(self.root, padx=5, pady=5)
frame2.pack(side='bottom')
self.button = []
for i, command in enumerate(commands):
self.button.append(Button(frame2, text=command.items()[0][0],
command=command.items()[0][1]))
self.button[i].grid(row=0, column=i)
self.root.mainloop()
class Main(object):
def __init__(self):
import sys
self.sp = SetParameter()
self.dla = None
self.b = None
self.sp.show_setting_window([{'N': 200}],
[{'a': self.exp_a},
{'b': self.exp_b},
{'c': self.exp_c},
{'c:fit': self.fitting},
{'save': self.pr},
{'quit': sys.exit}])
def exp_a(self):
self.N = int(self.sp.entry[0].get())
self.dla = DLA(self.N)
lattice = self.dla.grow_cluster()
def exp_b(self):
trial = 3000
self.dla2 = DLA(2, view=False)
self.dla2.L = 6
distribution = {'p': 0, 'q': 0, 'r': 0, 's': 0}
# 分類
for i in range(trial):
lattice = self.dla2.grow_cluster()
l = lattice[self.dla2.L-1:self.dla2.L+2,
self.dla2.L-1:self.dla2.L+2]
if np.sum(l) == 2:
distribution['r'] += 1
elif np.sum(l[0,1]+l[1,0]+l[1,2]+l[2,1]) == 1:
distribution['p'] += 1
elif max(max(np.sum(l, 0)), max(np.sum(l, 1))) == 3:
distribution['s'] += 1
else:
distribution['q'] += 1
for k, v in distribution.items():
distribution[k] = float(v)/trial
distribution['p'] = distribution['p']/2.
distribution['q'] = distribution['q']/2.
print 'trial = %d' % trial
print distribution
def exp_c(self):
self.N = int(self.sp.entry[0].get())
self.dla3 = DLA(self.N, view=False)
self.lattice = self.dla3.grow_cluster()
self.view_expansion()
self.plot()
def view_expansion(self):
lattice = self.lattice
center = self.dla3.center
M_b = []
s = np.sum
ave = np.average
append = M_b.append
for k in range(1, center):
nonzero = np.nonzero(lattice[k:-k,k:-k])
tmp = np.array([0])
for i, j in zip(nonzero[0]+k, nonzero[1]+k):
tmp = np.append(tmp, s(lattice[i-k:i+k+1, j-k:j+k+1]))
append(ave(tmp))
self.b = np.array([2.*k+1 for k in range(1, center)])
self.M_b = np.array(M_b)
def plot(self):
fig = plt.figure("Fractal Dimension")
self.ax = fig.add_subplot(111)
self.ax.plot(self.b, self.M_b, '-o')
self.ax.set_xlabel(r'$b$', fontsize=16)
self.ax.set_ylabel(r'$M(b)$', fontsize=16)
self.ax.set_xscale('log')
self.ax.set_yscale('log')
self.ax.set_ymargin(0.05)
fig.tight_layout()
plt.show()
def fitting(self):
if self.b == None:
return
import scipy.optimize as optimize
def fit_func(parameter0, b, M_b):
log = np.log
c1 = parameter0[0]
c2 = parameter0[1]
residual = log(M_b) - c1 - c2*log(b)
return residual
def fitted(b, c1, D):
return np.exp(c1)*(b**D)
cut_from = int(raw_input("from ? (index) >>> "))
cut_to = int(raw_input("to ? (index) >>> "))
cut_b = np.array(list(self.b)[cut_from:cut_to])
cut_M_b = np.array(list(self.M_b)[cut_from:cut_to])
parameter0 = [0.1, 2.0]
result = optimize.leastsq(fit_func, parameter0, args=(cut_b, cut_M_b))
c1 = result[0][0]
D = result[0][1]
self.ax.plot(cut_b, fitted(cut_b, c1, D),
lw=2, label="fit func: D = %f" % D)
plt.legend(loc='best')
plt.show()
def pr(self):
import tkFileDialog
import os
if self.dla is None:
print "first you should run 'a'."
return
fTyp=[('eps flle','*.eps'), ('all files','*')]
filename = tkFileDialog.asksaveasfilename(filetypes=fTyp,
initialdir=os.getcwd(),
initialfile="figure_1.eps")
if filename == None:
return
self.dla.canvas.postscript(file=filename)
if __name__ == '__main__':
Main()