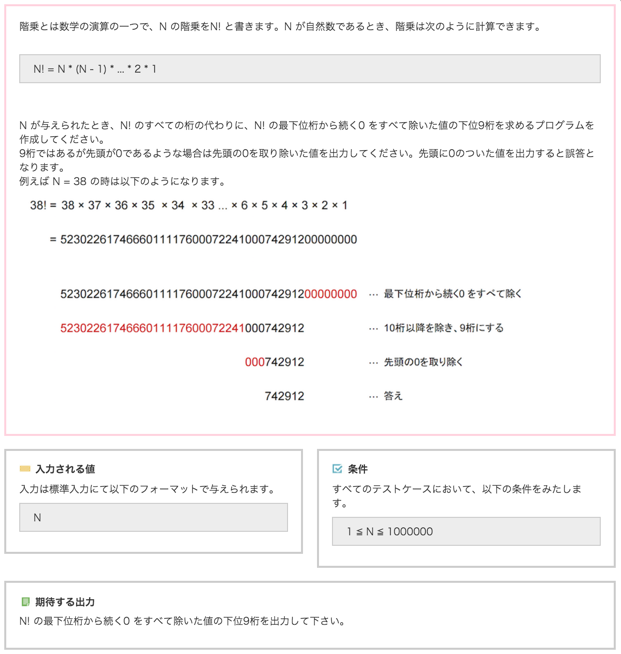
きっかけ
先日のことです。研究室の数人が 水着 に熱くなっていました。
というのも、paizaオンラインハッカソンの第7弾はプログラミンの問題を解いていくことでバーチャル彼女の着せ替え用アイテムがゲットできるというものでした。
水着 をゲットするため、問題にチャレンジです。
問題
みんなが水着をゲットしていく中、僕は全くできませんでした。。
僕「みんな、なんでそんなにスラスラ書けるんだ?」
後輩「慣れてる言語でやってるからですよ!」
僕「(慣れてる言語なんて僕にはないです、すいません)」 ![]()
頭でアルゴリズムを考えながら、コーディングするなんてそんな高度なことできませんでした。
(精進します汗)
チャレンジ
漠然とした方針
$ N! $ の素因数分解を考えてみます。
$$
N! = 2^{a} \cdot 3^{b} \cdot 5^{c} \cdot \dotsm
$$
とした時、 $ a > c $ なので(帰納法で証明できます。)
\begin{align}
N! &= M \cdot 2^{a-c} \cdot 10^{c} & (M \in \mathbb{N} ) \\
&= M' \cdot 10^{c} & (M' = M \cdot 2^{a-c}) \\
\end{align}
ここで、求めたいものは $ M' $ の下9桁です。
つまり、計算の過程で割り算が無ければ、下9桁同士の掛け算が正確に行えればいいので、18桁まで扱える変数があれば、特にオーバーフローは気にしなくていいのかな、と思いました。
ここで、符号なし 64-ビット 整数 が $ 0 〜 約18 \times 10^{18} $ なので、常に $ 10^{9} $ の余りを求め、且つ、割り算を使わず、 $ M' $ を直接求めれば、下9桁ならいけるだろうと思いました。
ここら辺情報系なのによくわかってないです。
数学的な方針
ここで、自然数 $ N $ が与えられた時に5の倍数以外の階乗を求める関数 $ f ( N ) $ を考えます。
$$
f (N) = \prod_{i \neq 5m}^{N} i ( m \in \mathbb{N} )
$$
$ N = 38 $ の時を考えてみます。
\begin{align}
38! &= f(38) \cdot 5 \cdot 10 \cdot 15 \cdot 20 \cdot 25 \cdot 30 \cdot 35 \\
&= f(38) \cdot 5^{7} \cdot 7! \\
\end{align}
ここで、 $ 7 = \left[ \frac{38}{5} \right] $ で $ 38 $ の中の $ 5 $ の倍数の数です。
$ 7! $ に関しても再帰的に $ f $ を用いると
\begin{align}
38! &= f(38) \cdot 5^{7} \cdot f(7) \cdot 5^{1} \cdot f(1) \\
\end{align}
ここで、 $ 1 = \left[ \frac{7}{5} \right] = \left[ \frac{38}{5^{2}} \right] $ で $ 38 $ の中の $ 25 $ の倍数の数です。
また、 $ 8 = 7 + 1 $ は $ 38! $ の中の $ 5 $ の因数の数です。
ここで、求めたい $ M' $ は
\begin{align}
M' &= \frac{N!}{10^{c}} & \\
&= \frac{38!}{10^{8}} & ( N = 38, c = 8 ) \\
&= \frac{38!}{2^{7} \cdot 5^{7} \cdot 2^{1} \cdot 5^{1}} & \\
\end{align}
$ f'(N) = \frac{f(N)}{2^{[ \frac{N}{5} ] }} $ とおくと、
\begin{align}
M' &= f'(38) \cdot f'(7) \cdot f'(1) & ( 2^{0} = 1 ) \\
&= \prod_{i=0}^{k} f' \left( \left[ \frac{N}{5^{i}} \right] \right) & ( 5^{k+1} > N \geq 5^{k} )
\end{align}
となります。
$ f' $ が割り算をしているのが気になりますが、この時点の実装でチャレンジは通りました。
$ M' = \dotsm \cdot f'(5) \cdot f'(1) $ で終わって、且つ、10桁以上になるような数、例えば $ N = 125 $ なんかではうまくいかないんじゃないかなと懸念しましたが。
でも、もういいです。
実装
こんな感じでした。
package main
import "fmt"
func main() {
var N uint64
fmt.Scan(&N)
var fact uint64 = 1
for N >= 5 {
fact = (fact * FactorialExceptingMultiple5(N)) % 1000000000
N = N / 5
}
fact = (fact * FactorialExceptingMultiple5(N)) % 1000000000
fmt.Printf("%d\n", fact)
}
func FactorialExceptingMultiple5(n uint64) (fact uint64) {
fact = 1
var i uint64 = 1
for i <= n {
if i%5 != 0 {
fact = (fact * i) % 1000000000
} else {
fact = fact / 2
}
i++
}
return
}
最後に
読んでくださった方ほんと中途半端で且つしょうもない内容でごめんなさい。
ちゃんとアルゴリズムとかプロコン系の勉強したいと思います。
こちらのページが Qiita で数式書くのに非常に助かりました。