Jupyter NotebookはPythonでプログラムを書いて可視化する際に、非常に便利なツールです。
Pythonにはデータ分析や数値計算、可視化を行うためのライブラリが多くあるため、相性がとても良いです。
一方で、データ分析の世界には、離散的なデータの集合から本来のデータの形を知るための手法として、位相的データ解析(Topological Data Analysis)と呼ばれるものがあります。
ここでは、位相的データ解析で利用されるアルファ複体のフィルトレーションをJupyter Notebookで可視化する方法について紹介します。
前半では、位相的データ解析やそこで利用する手法を説明します。雰囲気を伝えることを優先しているので、数学用語の厳密な説明はしていません。
後半では、具体的にアルファ複体のフィルトレーションの可視化を行います。
位相的データ解析とは?
位相的データ解析は、ここ10数年で急速に発展してきたデータ解析手法です。
ノイズを含んだ離散的なデータの集合から元のデータの形を知るための手法で、トポロジー(topology)という分野の数学を利用しています。
トポロジーは図形を伸び縮みさせて変形させても変わらない性質を扱う数学の分野です。
図形が作る単体複体(simplicial complex)という数学的対象からホモロジー群(homology group)と呼ばれるものを導くことで、図形の連結成分の数や穴の数を計算すことができます。(「穴の数」のような、「見た目」の情報とも思えるものを数学的に扱えるようにしているのが、トポロジーの素晴らしいところだと思います)
「図形」という見た目の情報から、コンピュータで計算可能な情報を取り出すのがミソです。
位相的データ解析では、次に挙げた流れに沿って入力から出力を導きます。
- 入力:離散的なデータの集合
- 単体複体のフィルトレーション
- ホモロジー群のフィルトレーション
- 出力:パーシステント図(データの形)
次のスライドは、一般向けに位相的データ解析を紹介されたものです。
位相的データ解析の考え方から、タンパク質の分類やセンサーネットワークの被覆問題への応用まで触れられています。
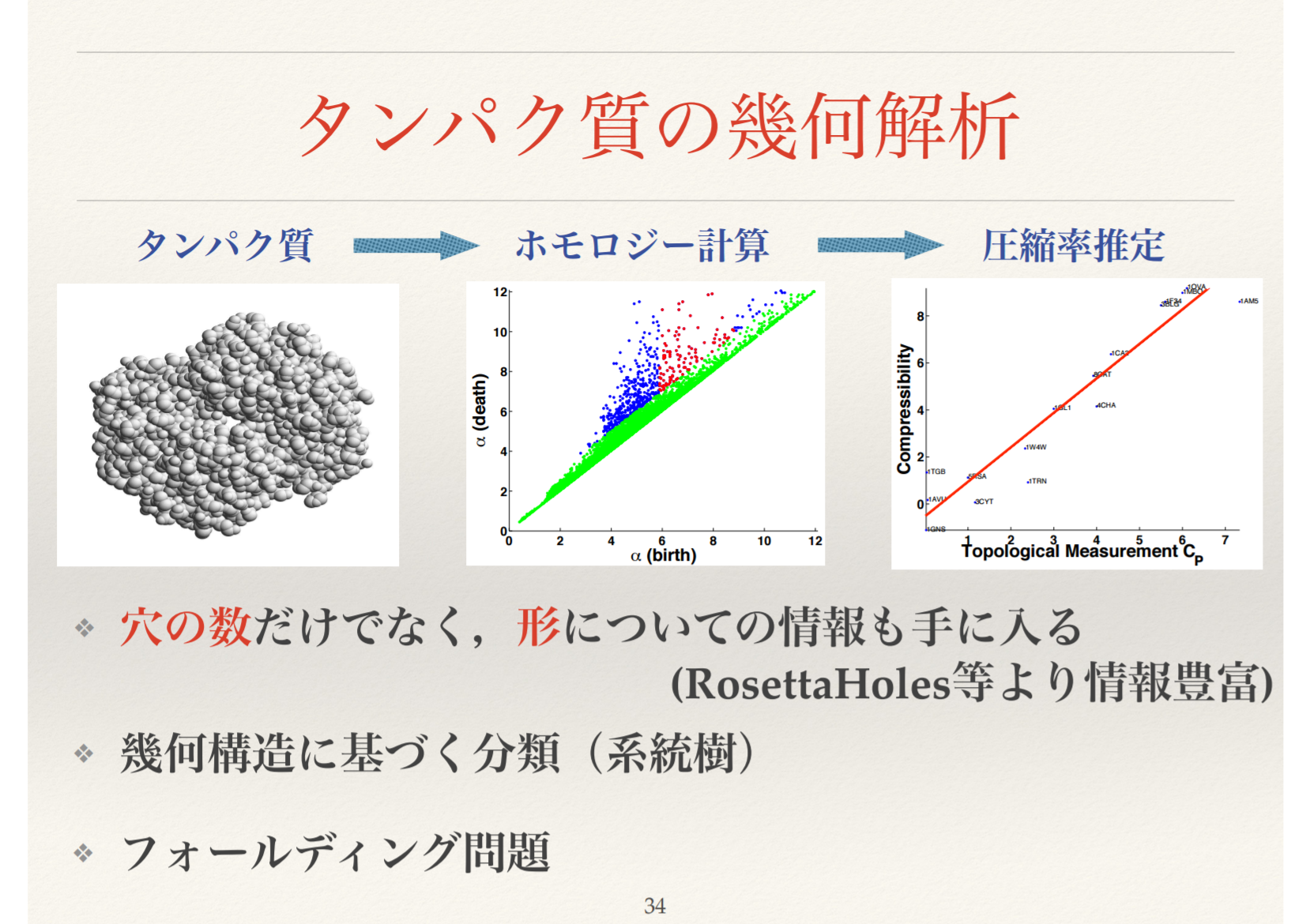
スライドから引用させて頂くと、次の「タンパク質」の部分が入力で、「ホモロジー計算」の部分が出力になります。
位相的データ解析について、詳しく知りたい方は次のページのリンク先をご覧ください。
単体複体のフィルトレーション
位相的データ解析の計算は、離散的なデータの集合から単体複体のフィルトレーションを導出するところから始まります。
離散的なデータの集合は座標をもった単なる点の集まりです。
これに対して、単体複体と呼ばれる構造を入れます。
選択する単体複体にはいくつか種類があるのですが、アルファ複体(alpha complex)は計算量が少ないことで知られています。
$m$ 個の点からなるデータの集合が $\mathbb{R}^n$ に存在するとき、チェック複体などの単体複体の次元は最大で $m$ になる可能性があります。
しかし、アルファ複体だと次元が $n$ 以下になるため、少ない計算量で導出することができます。
私たちの住んでいる空間が3次元のため、「$m=1000$ 以上、$n=2, 3$ 」の問題を扱うことは多いのではないでしょうか。
また、アルファ複体は脈体定理(nerve theorem)というものが成立し、図形のトポロジー的な性質が保持されるため、都合の良い構成法になります。
次の図は
というサイトを参考にして、アルファ複体のフィルトレーションを可視化したものです。(私のプログラムのバグにより、ちょっとおかしいですが。。。)

左上の図がドロネー三角形分割(Delaunay triangulation)と呼ばれるものです。
与えられたデータの集合を赤い点で表していますが、そこからボロノイ図(Voronoi diagram)というものを作り、そこからさらに導き出されたものがドロネー三角形分割です。
「Alpha shape, alpha=xxx」という図が、アルファ複体のフィルトレーションと呼ばれるもので、xxxの数字を変えていくことで、連結成分の数や穴の数が変化していきます。
位相的データ解析では、「フィルトレーションで長く保たれている連結成分や穴は、ノイズでなく元のデータの形が表われたもの」と考えます。
連結成分や穴の保たれ方を可視化したものがパーシステント図(persistent diagram)というもので、最初の図で「ホモロジー計算」と書かれたものです。
2次元座標の点として、連結成分や穴をプロットしたもので、対角線から遠いものほど「フィルトレーションで長く保たれている」(=元のデータの形が表われている)ことを示します。
と、ここまで背景説明を行ってきました。
駆け足になってしまい、雰囲気を伝えられたか大いに心配ですが、、、
可視化ライブラリ
では、アルファ複体のフィルトレーションを可視化してみましょう。
ここでは、
というライブラリを利用します。
このライブラリを使うと、Pythonを利用して様々な可視化を行うことができます。
利用方法によっては、APIキーの登録が必要になる場合があります。
もう一度掲載しますが、アルファ複体を構成する際の半径の値を0.10から0.18まで、0.02ずつ変えたときのアルファ複体を可視化したものが、次の図になります。

Jupyter Notebookを利用して、これを具体的に可視化してみましょう。
具体的にどのようなコードを書けばよいの?
(かなり端折っているので、後ほど更新します。。。)
Plotlyにあるアルファ複体のサンプルを参考にするのがオススメです。
私はこのコードをベースに先ほど紹介した図を書きました。
Notebook形式で次の場所に公開しています。
最後に
こういう計算・可視化を簡単に再現でき、過程・結果を共有できるのが、Jupyter Notebookの良い点ですね。
学術論文の付録にNotebookを添付することが増えれば、最新理論の普及も速くなるのでは、と個人的には考えています。